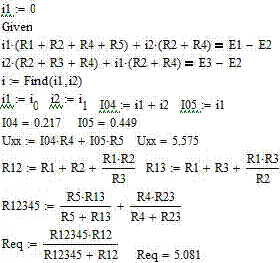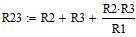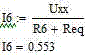Расчет линейной электрической цепи постоянного тока
Задание 1.
Для электрической схемы, изображенной на рисунке 1, где E1 = 16 В,
E2 = 8 В, E3 = 9 В, R1 = 2,5 Ом, R2 = 6 Ом, R3 = 6 Ом, R4 = 5 Ом, R5 = 10 Ом,
R6 = 5 Ом, выполнить следующее:
1) составить и решить систему уравнений, необходимых для определения токов по первому и второму законам Кирхгофа;
2) найти токи в ветвях, пользуясь методом контурных токов;
3) проверить правильность решения, применив метод узловых потенциалов;
4) определить ток в резисторе R6 методом эквивалентного генератора;
5) определить показание вольтметра и составить баланс мощностей;
6) построить в масштабе потенциальную диаграмму для внешнего контура.
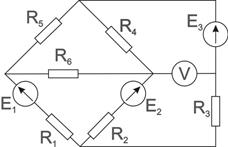
Рисунок 1 – схема электрической цепи постоянного тока
Расчет линейной электрической цепи постоянного тока
Выберем направления токов в ветвях электрической цепи, представленной на рисунке 4, а также обозначим все узлы цепи буквенными обозначениями.
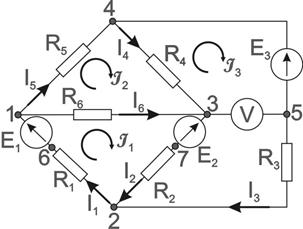
Рисунок 4 – Расчетная схема электрической цепи
1) Составим 3 уравнения по первому закону Кирхгофа,
n
) Ik = 0 (1)
k=1
Выбираем произвольные направления обхода контуров. Составляем 3
уравнения для независимых контуров по второму закону Кирхгофа:
m n
) RkIk = ) Ek
(2)
k=1 k=1
Объедением и совместно решаем систему уравнений (1) и (2) для определения токов в ветвях схемы. Если для какого-либо тока будет получено отрицательное значение, то из этого следует, что его действительное направление противоположно выбранному.
Имеем систему уравнений:
I1 − I5 − I6 = 0
fI2− I1+ I3= 0
|
6 − I2
− I4 = 0
(3)
IR5I5− R4I4− R6I6= 0 IR1I1+ R6I6+ R2I2= E1− E2hR2I2 − R3I3 − R4I4 = E3 − E2
Решение дает: I1=0,846 А, I2=0,520 А, I3=0,326 А, I4=0,033 А, I5=0,293 А,
I6=0,533 А.
2) Составим 3 уравнения по второму закону Кирхгофа (2) для обозначенных на рисунке 4 контурных токов.
Получим систему уравнений:
ℐ1(R1 + R6 + R2) − ℐ2R6 − ℐ3R2 = E1 − E2
{ℐ2(R5 + R4 + R6) − ℐ3R4 − ℐ1R6 = 0
ℐ3(R2 + R3 + R4) − ℐ2R4 − ℐ1R2 = E2 − E3
Решая ее, получаем: I1= 0,846 А , I2= 0,293 А, I3= 0,326 А.
(4)
Токи в ветвях определяются как алгебраическая сумма контурных токов, проходящих через данную ветвь, вычисляя, получим:
I1=0,846 А, I2=0,520 А, I3=0,326 А, I4=0,033 А, I5=0,293 А, I6=0,533 А.
3) Заменим все сопротивления на проводимости:
G = R (5)
G1=0,4 Cм, G2=0,167 Cм, G3=0,167 Cм, G 4=0,2 Cм, G 5=0,1 Cм, G 6=0,2 Cм.
Выберем узел 3 в качестве базового, т.е. его потенциал равен нулю:
n n n
" ) Gi− ) "iGi= ) EiGi + Ji
(6)
i=1
i=1
i=1
Для каждого узла (1,2,4) составляем уравнение по формуле (6): потенциал умножаем на сумму проводимостей ветвей, прилегающих к узлу, и вычитаем произведения потенциалов соседних узлов на проводимость ветвей, соединяющих его с данным узлом; все это приравниваем к сумме источников тока и источников напряжения помноженных на проводимости соответствующих ветвей. Получим систему уравнений:
"1(G1 + G5 + G6) − "2G1 − "4G5 = E1G1
{"2(G1 + G2 + G3) − "1G1 − "4G3 = −E1G1−E2G2−E3G3 "4(G3 + G4 + G5) − "1G5 − "2G3 = E3G3
Решая систему, получаем следующие значения потенциалов:
φ1=2,765 В, φ2=-11,120 В, φ3=0 В, φ4=-0,165 В.
(7)
Определим потенциалы для остальных точек. Для этого отнимаем от потенциалов соседних точек, к которым направлено ЭДС, значение этого ЭДС: φ5= φ4 - Е3, φ6= φ1 – Е1, φ7= φ3 - Е2. Получаем следующие значения:
φ5 = -9,165 В, φ6 = -13,235 В, φ7 = -8 В.
Токи в ветвях находим как произведения проводимости ветви на сумму падения напряжения на ветви и ЭДС, тогда
I1=0,846 А, I2=0,520 А, I3=0,326 А, I4=0,033 А, I5=0,293 А, I6=0,533 А.
4) Определим ток в резисторе R6 методом эквивалентного источника напряжения. Для этого вычленим из цепи, изображенной на рисунке 4, резистор R6 и приложим напряжение холостого хода Uхх (рисунок 5), тогда искомый ток определится как:
I6 = R
Uхх
+ R
, (8)
6 э
где Rэ – эквивалентное сопротивление цепи относительно резистора R6 при отсутствии в цепи генераторов, представленной на рисунке 6.
 |
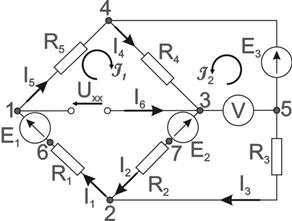Рисунок 5 – Расчетная схема для метода эквивалентного генератора
Составим уравнения по формуле (2) для контурных токов I1 и I2.
ℐ1(R1 + R2 + R4 + R5) + ℐ2(R2 + R4) = E1 − E2
|
2(R2
+ R3
+ R4
) + ℐ1
(R2
+ R4
) = E3
− E2
(9)
Решая, получим I1 = 0,449 А и I2 = -0,232 А. Тогда токи I5 = I1 = 0,449 А, I4 = I1 + I2 = 0,217 A.
Падение напряжения на участке 1-4-3, равное Uхх определится как:
Uss = I5R5+ I4R4 (10)
Вычисление дает Uхх = 5,575 В.
 |
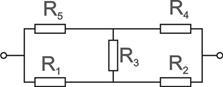Рисунок 6 – Схема для расчета эквивалентного сопротивления
Преобразуем соединение «звезда» резисторов R1, R3, R2 в соединение резисторов «треугольник» по формулам (11):
R12 = R1 + R2 + R13 = R1 + R3 + R23 = R2 + R3 +
R1 + R2 R3
R1 + R3 R2
R2 + R3 R1
(11)
Получаем схему, изображенную на рисунке 7 и значения новых сопротивлений R12 = 11 Ом, R13 = 11 Ом, R23 = 26,4 Ом.
 |
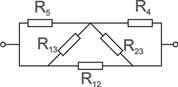Рисунок 7 – Схема для расчета эквивалентного сопротивления после преобразования «звезда – треугольник»
Очевидно, что пары резисторов R13 и R5, R23 и R4 соединены параллельно, а между собой пары соединены последовательно, образуя с R12 параллельное соединение:
Rэ =
( R5R13 R5 + R13
R5R13
+ R4R23 R4 + R23
R4R23
) R12
(12)
R5 + R13 + R4 + R23 + R12
Итого получаем Rэ = 5,081 Ом.
Подставляя значения, полученные при вычислении (10) и (12), в (8),
получаем: I6 = 0,553A.
5) Показания вольтметра определим как разность потенциалов между точками 3 и 5:
UV = φ3 - φ5 = 9,165 В.
Рассчитаем выделенную источниками энергию в единицу времени по формуле:
n m
P1= ) ±EiIi+ ) JiUi
(13)
i=1 i=1
Если направление тока I, протекающего через источник ЭДС Е совпадает с направлением ЭДС, то источник ЭДС доставляет в цепь в единицу времени энергию, равную произведению Е·I и входит с положительным знаком в уравнение энергетического баланса. Если направление тока I не совпадает с направлением ЭДС, то перед произведением E·I ставим знак «–».
Вычисления дают: P1 = 6,442 Вт.
Рассчитаем выделившуюся на сопротивлениях мощность по формуле:
n
|
i=1
(14)
Вычисления дают P2 = 6,442 Вт.
P1 = P2 – уравнение энергетического баланса выполняется: мощность, выделяемая источниками напряжения численно равна тепловой мощности, выделяемой на сопротивлениях.
6) Строим потенциальную диаграмму, отмечая по оси ординат потенциалы точек в порядке 1-4-5-2-6-1, а по оси абсцисс суммарное сопротивление пройденного участка. Диаграмма показана на рисунке 8.
 |
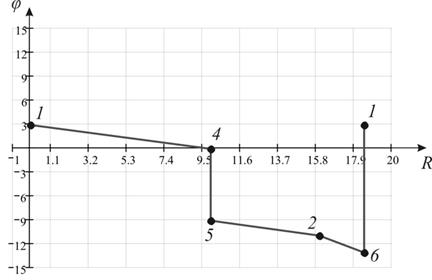Рисунок 8 – Потенциальная диаграмма для внешнего контура
Расчет задания в программной оболочке MathCAD приведен ниже.
Дано
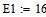
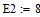
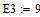
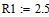
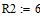
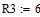
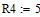
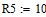
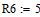
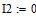
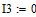
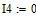
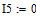
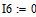Определяем все токи используя законы Кирхгофа
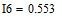
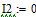
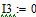
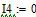
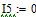
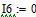
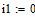
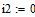
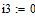Определяем все токи методом контурных токов
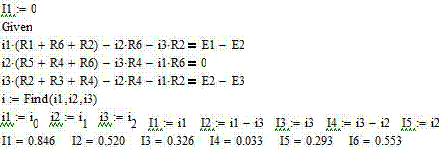
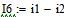
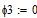
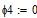Определяем все токи методом узловых потенциалов
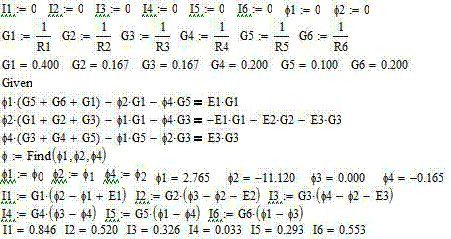
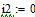
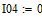
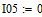
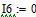Определяем ток в резисторе R6 методом эквивалентного генератора
