Решение систем уравнений, заданных в векторном виде

Весьма мощным средством символьной математики Mathcad является возможность решения систем нелинейных уравнений, заданных в векторной форме, с помощью директивы solve. Такая форма очень наглядна, особенно с примерами решения с помощью директивы solve для систем нелинейных уравнений, заданных в векторной форме. Обратите внимание, что при задании исходных уравнений в векторной форме результат решения также представляется в векторной форме. Это значит, что он может быть целиком или частично использован в ка­честве входного выражения для дальнейших символьных вычислений.

Теоретические вопросы, выносимые на обсуждение

1.Какие матричные опера­ции выполняет процессор системы Mathcad в символьном виде.

2.В чем состоит основная проблема при выполнении матричных операций в символьной форме.

3.Где расположены команды относящиеся к матричным опе­рациям.

4.Запишите команду транспонировать, что она означает.

5.Запишите команду обратить, что она означает.

6.Для какой матрицы операция обратить допустима.

7.Какую размерность имеет обращенная матрица.

8.Запишите команду опреде­литель, что она означает.

9.Запишите команду, определяющую собственные значения матрицы M, что она означает.

10. Дать определение канонического вида матрицы.

11. Опишите этапы алгоритма построения канонического вида матрицы.

12. Какой вид имеет диагональная матрица.

13. Какой вид имеет единичная матрица.

14. Какой вид имеет жорданова клетка.

15. Чем отличаются кратные и повторные собственные значения матрицы M.

16. Запишите уравнение на собственные значения матрицы M (характеристическое уравнение).

17. Какой предварительный анализ системы линейных уравнений необходимо сделать, чтобы решать ее в матричной форме.

18. Какие способы матричного метода вы знаете.

19. Опишите этапы алгоритма матричного метода 1-вым, 2-ым и 3-им способами.

20. Опишите этапы алгоритма метода Гаусса.

21. Опишите этапы алгоритма метода Крамара.

22. Можно ли решать системы линейных уравнений в символьном виде.

23. Можно ли решать нелинейные уравнения в символьном виде.

24. С помощью какой команды решаются нера­венства и нелинейные уравнения в символьном виде.

25. Перечислите, какие функции применяются при работе с нера­венствами и нелинейными уравнениями и что они обозначают.

26. Какие отличительные свойства имеет оператор символь­ного вывода.

27. В каком виде лучше решать системы нелинейных уравнений.

28. С помощью какой команды решаются нелинейные системы уравнений.

29. Если системы нелинейных уравнений записываются в векторном виде, то в каком виде получается результат.

Задания к вариантам для самостоятельных работ

I.Найти ранги матрицы

1.	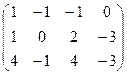2.	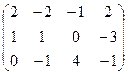3.	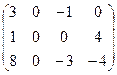4.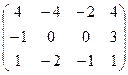
5.	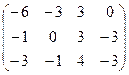6.	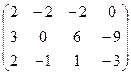7.	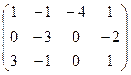8.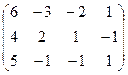
9.	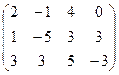10.	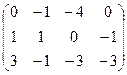11.	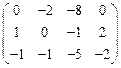12.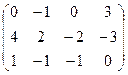
13.	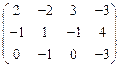14.	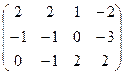15.	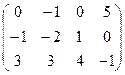16.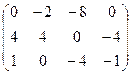

II Проверить, является ли система векторов линейно зависимой:

1. f₁=(2;-1;4;0), f₂=(-1;5;3;3), f₃=(0;-1;-2;-3)

2. f₁=(2;-1;-4;0), f₂=(1;-5;3;3), f₃=(0;-1;2;-3)

3. f₁=(1;-1;-1;0), f₂=(1;0;2;-3), f₃=(4;-1;4;-3)

4. f₁=(2;-2;-1;2), f₂=(1;1;0;-3), f₃=(0;-1;-4;-1)

5. f₁=(5;-1;-3;0), f₂=(1;0;0;3), f₃=(4;-1;-3;-6)

6. f₁=(4;-4;-2;4), f₂=(-1;0;0;3), f₃=(1;-2;-1;1)

7. f₁=(0;-1;0;3), f₂=(4;2;-2;-3), f₃=(1;-1;-1;0)

8. f₁=(2;-1;-4;0), f₂=(3;-15;9;9), f₃=(1;4;-7;-3)

9. f₁=(-2;-1;1;0), f₂=(-1;0;3;-3), f₃=(0;1;2;3)

10. f₁=(6;-1;-4;0), f₂=(1;0;0;3), f₃=(4;-1;-4;-6)

11. f₁=(2;-1;4;0), f₂=(1;-5;3;3), f₃=(3;3;5;-3)

12. f₁=(0;-1;-4;0), f₂=(1;1;0;-1), f₃=(3;-1;-3;-3)

13. f₁=(3;-1;-2;1), f₂=(-4;1;0;0), f₃=(0;0;-4;-6)

14. f₁=(0;-2;-8;0), f₂=(1;0;-1;2), f₃=(-1;-1;-5;-2)

15. f₁=(3;0;-1;0), f₂=(1;0;0;4), f₃=(8;0;-3;-4)

16. f₁=(1;-1;-1;1), f₂=(4;-3;2;-1), f₃=(-1;0;-5;4)

III Вычислить определитель матрицы и найти ей обратную:

1.	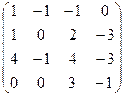2.	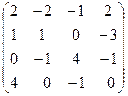3.	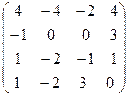4.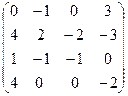
5.	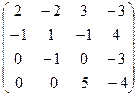6.	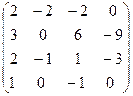7.	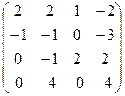8.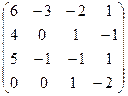
9.	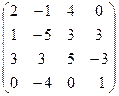10.	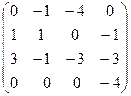11.	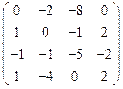12 .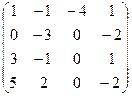
13.	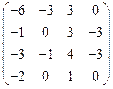14.	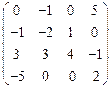15.	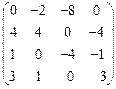16.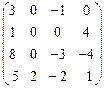

IV Решить систему уравнений тремя методами: матричный метод, метод Гаусса, метод Крамара. Провести сравнительную характеристику этих методов.

1.	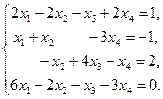2.	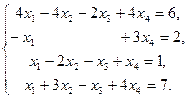3.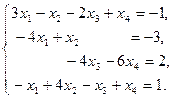
4.	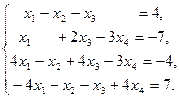5.	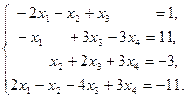6.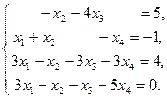
7.	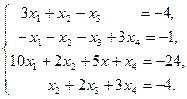8.	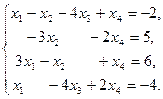9.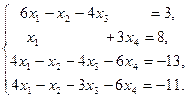
10.	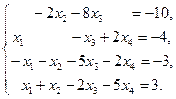11.	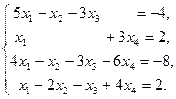12.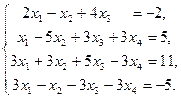
13.	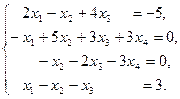14.	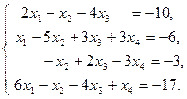15.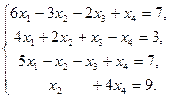
16.

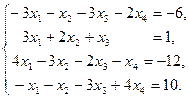V Привести матрицу к каноническому виду

1.	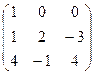2.	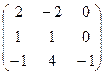3.	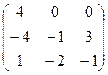4.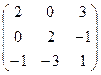
5.	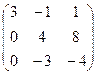6.	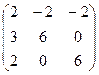7.	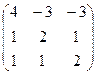8.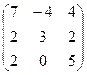
9.	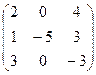10.	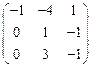11.	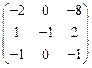12.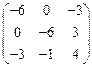
13.	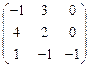14.	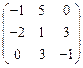15.	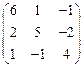16.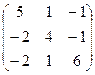

Практическое занятие № 4