Тема 2. ИССЛЕДОВАНИЕ ЧАСТОТНЫХ ХАРАКТЕРИСТИК СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
Цель работы
Изучение методики получения частотных характеристик систем автоматического управления (САУ) по известным передаточным функциям.
Программа работы
1. Изучение теоретических основ вычисления частотных характеристик САУ.
2. Составление и отладка программ вычисления полиномов B(w), C(w), d(w), E(w) по схеме Горнера.
3. Построение графиков частотных характеристик САУ.
4. Выводы.
Теоретические основы работы
Частотные характеристики нашли широкое применение при анализе и синтезе САУ, так как позволяют косвенно, т.е. без решения дифференциальных уравнений, судить об устойчивости и основных показателях качества, а также выбирать структуру и параметры корректирующих устройств, необходимых, для выполнения предъявленных к системе технических требований [1]. Существуют различные методы построения частотных характеристик как аналитическим, так и экспериментальным способом. Наиболее простым из них является метод получения частотных характеристик по известным передаточным функциям путём формальной замены переменной p на 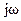 , где j=√-1,
, где j=√-1,  Пусть передаточная функция исследуемой системы имеет вид:
Пусть передаточная функция исследуемой системы имеет вид:
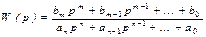 , при
, при 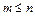

Полагая 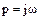 , где
, где 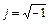 , получаем:
, получаем:
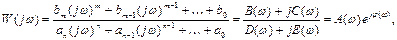 (2.1)
(2.1)
Выражение (1) называется частотной передаточной функцией или амплитудно-фазовой частотной характеристикой (АФЧХ).
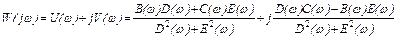 , (2.2)
, (2.2)
где 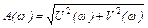 - амплитудно-частотная характеристика;
- амплитудно-частотная характеристика;
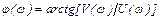 - фазочастотная характеристика.
- фазочастотная характеристика.
Вычисление каждого из четырех полиномов 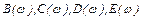 можно организовать по схеме Горнера [2], которую продемонстрируем на следующем примере. Пусть дан полином n-й степени с действительными коэффициентами
можно организовать по схеме Горнера [2], которую продемонстрируем на следующем примере. Пусть дан полином n-й степени с действительными коэффициентами 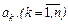 :
:
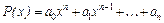 .
.
Положим, что требуется найти 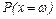 :
:
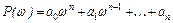 .
.
Представим
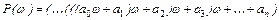 ,
,
тогда 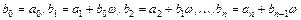 , т.е.
, т.е.  .
.
Порядок выполнения работы
1. По известной передаточной функции системы определить частотную передаточную функцию путем замены переменной p на 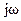 , и представить ее в виде выражения (2.2).
, и представить ее в виде выражения (2.2).
2. Для вычисления полиномов 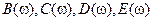 применить схему Горнера. Составить программу расчета. При этом начальный шаг
применить схему Горнера. Составить программу расчета. При этом начальный шаг 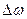 может быть определен, например, по правилу
может быть определен, например, по правилу 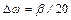 , где
, где 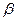 - мнимая часть корня характеристического уравнения, ближайшего к мнимой оси.
- мнимая часть корня характеристического уравнения, ближайшего к мнимой оси.
3. Для каждого значения 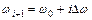 вычислить
вычислить 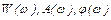 , причем выходную информацию выдать на печать в виде таблицы.
, причем выходную информацию выдать на печать в виде таблицы.
4. Построить графики 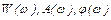 .
.
5. Построить графики 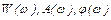 с использованием пакета MatCad или MatLab.
с использованием пакета MatCad или MatLab.
6. Сделать выводы.
Варианты заданий
Варианты заданий приведены в табл. 2.1.
Таблица 2.1
| № варианта | a0 | a1 | a2 | a3 | a4 | a5 | b0 | b1 | b2 | b3 | b4 | b5 |
| 115,5 | 64,9 | 26,15 | 15,43 | 3,48 | 0,1 | 22,02 | 14,26 | -11,1 | 2,06 | 4,97 | 3,62 | |
| 89,05 | 61,06 | 82,07 | -3,17 | 12,35 | 6,09 | - | 4,16 | 2,35 | 4,16 | -25,7 | 11,6 | |
| 111,2 | 4,12 | 2,35 | 41,27 | 4,98 | 0,5 | 5,25 | 4,16 | 28,02 | 4,27 | 3,14 | -2,68 | |
| 34,27 | -4,68 | 2,57 | 13,49 | 4,29 | 5,67 | 2,68 | -5,49 | 4,18 | 2,16 | 3,48 | - | |
| 18,25 | 4,77 | 3,66 | -12,4 | 7,35 | 0,17 | 5,14 | 2,35 | -1,69 | 2,04 | -4,07 | - | |
| 4,98 | 3,15 | -2,36 | 4,89 | 11,02 | 6,48 | 2,56 | 2,42 | 16,68 | 30,02 | 12,52 | 0,68 | |
| 32,02 | 16,58 | 4,11 | -2,35 | 2,69 | - | 16,52 | 0,97 | 1,02 | 16,01 | -3,07 | - | |
| 39,84 | 26,07 | -15,2 | 11,25 | 4,92 | - | 5,26 | -1,39 | 6,85 | 11,69 | -4,52 | - | |
| 83,07 | 14,25 | -5,25 | 4,97 | 5,29 | 3,02 | 46,11 | 52,35 | -5,29 | -6,97 | - | - | |
| 114,2 | -5,35 | 2,69 | -17,3 | 2,55 | 4,08 | - | 5,26 | 4,97 | 52,17 | 98,58 | - |
6. Содержание отчёта.
1. Постановка задачи.
2. Краткая теория.
3. Алгоритм решения задачи.
4. Описание программы расчетов.
5. Результаты решения задачи.
6. Список используемой литературы.
Литература.
1. Бессекерский В.А., Попов Е.П. Теория систем автоматического регулирования. – М.: Наука, 1972. – 767с.
2. Демидович Б.П., Марон И.А. Основы вычислительной математики. – М.: Наука, 1970. – 659с.
