Условия равновесия плоской системы сил

На тело действует плоская система сил. Расположим оси Ox и Oy в плоскости действия сил.

Уравнения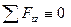

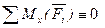
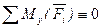
Для равновесия плоской системы сил, действующих на твердое тело, необходимо и достаточно, чтобы суммы проекций этих сил на каждую из двух прямоугольных осей координат, расположенных в плоскости действия сил, были равны нулю и сумма моментов этих сил относительно любой точки, находящейся в плоскости действия сил также была равна нулю.

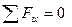
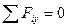
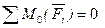
Теорема о трех моментах.

Для равновесия плоской системы сил, действующих на твердое тело, необходимо и достаточно, чтобы суммы моментов этих сил системы относительно трех любых точек, расположенных в плоскости действия сил и не лежащих на одной прямой, были равны нулю.

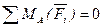
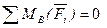
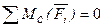
Статически определимые и статически неопределимые задачи.

Для любой плоской системы сил, действующих на твердое тело, имеется три независимых условия равновесия. Следовательно, для любой плоской системы сил из условий равновесия можно найти не более трех неизвестных.

В случае пространственной системы сил, действующих на твердое тело, имеется шесть независимых условия равновесия. Следовательно, для любой пространственной системы сил из условий равновесия можно найти не более шести неизвестных.

Задачи, в которых число неизвестных не больше числа независимых условий равновесия для данной системы сил, приложенных к твердому телу, называются статически определимыми.

В противном случае задачи статически неопределимы.

Равновесие системы тел.

Рассмотрим равновесие сил, приложенных к системе взаимодействующих между собой тел. Тела могут быть соединены между собой с помощью шарниров или иным способом.

Силы, действующие на рассматриваемую систему тел, можно разделить на внешние и внутренние.

Внешними называются силы, с которыми на тела рассматриваемой системы действуют тела, не входящие в эту систему сил.

Внутренними называются силы взаимодействия между телами рассматриваемой системы.

При рассмотрении равновесия сил, приложенных к системе тел, можно мысленно расчленить систему тел на отдельные твердые тела и к силам, действующим на эти тела, применить условия равновесия, полученные для одного тела. В эти условия равновесия войдут как внешние, так и внутренние силы системы тел. Внутренние силы на основании аксиомы о равенстве сил действия и противодействия в каждой точке сочленения двух тел образуют равновесную систему сил.

Покажем это на примере системы двух тел и плоской системы сил.

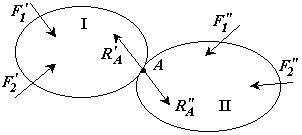Если составить условия равновесия для каждого твердого тела системы тел, то для тела I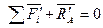

.

для тела II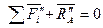

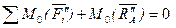
Кроме того, из аксиомы о равенстве сил действия и противодействия для двух взаимодействующих тел имеем .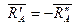

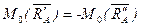Представленные равенства и есть условия равновесия внешних сил, действующих на систему.

Реакция заделки.

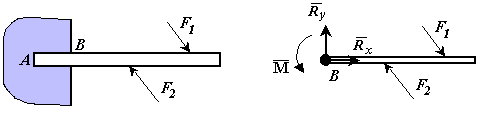Рассмотрим балку один конец которой АВ заделан в стену. Такое крепление конца балки АВ называется заделкой в точке В. Пусть на балку действует плоская система сил. Определим силы, которые надо приложить к точке В балки, если часть балки АВ отбросить. К сечению балки (В) приложены распределенные силы реакции. Если эти силы заменить элементарными сосредоточенными силами и затем привести их к точке В, то в точке В получим силу 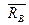(главный вектор сил реакции) и пару сил с моментом М (главный вектор сил реакции относительно точки В) . Момент М называют моментом заделкиилирективным моментом.Силу реакции 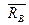можно заменить двумя составляющим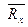и и .

Заделка в отличие от шарнира создает не только неизвестную по величине и направлению реакцию 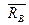, но еще и пару сил с неизвестным моментом М в заделке.