Методика измерения параметров тренда

Цель работы

1. Изучить методы укрупнения интервалов, скользящей средней и аналитического выравнивания для выявления тренда в рядах динамики.

2. Изучить методику расчета параметров трена в рядах динамики.

3. Сформировать практические навыки расчета параметров уравнения тренда динамического ряда.

4. Построить уравнение тренда динамического ряда и провести статистический анализ значимости его параметров.

Краткая теория

Ряд динамики – числовые значения статистического показателя, представленные во временной последовательности. Он состоит из двух граф: 1) в первой указывают периоды (даты); 2) во второй указывают показатели, характеризующие данный объект за эти периоды (даты). Показатели второй графы называются уровнями ряда. Первый показатель называется начальным уровнем, последний – конечным.

Уровни ряда могут быть выражены абсолютными, средними или относительными величинами. Ряды динамики относительных и средних величин строятся на основе рядов абсолютных величин.

По времени ряды динамики разделяются на моментальные и интервальные.

Моментальный ряд динамики – ряд, уровни которого характеризуют состояние явления на определенные моменты времени. Примером такого ряда могут служить данные о численности населения РФ (млн. чел.) по состоянию на 1 января в разные года. Моментальные ряды нельзя суммировать, так как в каждом последующем уровне полностью или частично содержится значение предыдущего уровня.

Интервальный ряд динамики – ряд, уровни которого характе-ризуют размер явления за конкретный период времени. Примером такого ряда могут служить данные о динамике добычи нефти в РФ (млн. тонн) за определенный период. Интервальные ряды можно суммировать, так как значение предыдущего уровня не содержится в последующем. Это позволяет получать статистические данные за более длительный период времени.

Одна из задач статистики – определение в рядах динамики общей тенденции развития явления. На развитие явления во времени оказывают влияние факторы, различные по характеру и силе воздействия. Одни из них оказывают постоянное воздействие и формируют в рядах динамики определенную тенденцию развития. Воздействие других факторов может носить случайный характер. Поэтому при анализе динамики исследоваться должна основная тенденция, устойчивая на протяжении изучаемого этапа развития.

Основная тенденция развития (тренд) –плавное и устойчивое изменение уровня явления во времени, свободное от случайных колебаний.

С целью выявления тренда ряды динамики исследуются методами укрупнения интервалов, скользящей средней и аналитического выравнивания.

Метод укрупнения интервалов основан на укрупнении периодов времени, к которым относятся уровни ряда динамики. Например, ряд ежесуточного выпуска продукции заменяется рядом месячного выпуска продукции, который, в свою очередь, может быть заменен рядом квартального выпуска продукции. Для каждого укрупненного интервала вычисляются средние уровни ряда 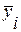по формуле простой арифмети-ческой средней. Например, если укрупненный интервал образован объединением трех периодов, эти величины равны:

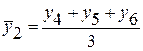; и т.д.,

где 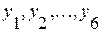– уровни исходного ряда динамики.

Сравнение рассчитанных таким образом средних позволяет выявить направление и характер (ускорение или замедление роста) основной тенденции развития, но не математическую модель тренда.

Метод скользящей средней основан на расчете средней величины, которая вычисляется по ряду при последовательном передвижении на один интервал, т.е. сначала вычисляют средний уровень из определенного числа первых по порядку уровней ряда, затем – средний уровень из такого же числа членов, начиная со второго и т.д. Например, скользящие средние с продолжительностью периода, равной 3, вычисляются как:

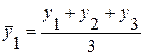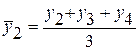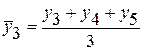; ; и т.д.

Таким образом, средняя как бы «скользит» по ряду динамики. Если в ряду динамики имеются периодические колебания, то период скользящей средней совпадает с периодом колебания или будет кратным ему. Метод позволяет выявить направление и характер основной тенденции развития, но не математическую модель тренда.

Метод аналитического выравнивания – наиболееэффективный способ выявления основной тенденции развития. Он позволяет определить аналитическое выражение, отражающее закономерность изменения явления как функцию времени 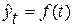, где t – условное обозначение времени. Например,

год
t

Метод аналитического выравнивания основан на замене факти-ческих значений уровней 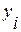плавно изменяющимися величинами . Аналитическое выравнивание может быть осуществлено по любому рациональному многочлену (см. табл. 7.3). Выбор функции производится, во-первых, на основе анализа характера закономерностей динамики данного явления.

1. При равномерном развитии явления во времени используется полином 1-й степени (прямая): 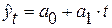. В этом случае абсолютные приросты 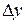(первые разности) практически постоянны. При 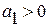уровни динамики равномерно возрастают, при 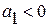– равномерно снижаются. Линейный тренд хорошо отражает тенденцию изменений при действии множества факторов, изменяющихся по разным закономерностям, что приводит к взаимопогашению особенностей отдельных факторов. Примером могут служить тенденции динамики урожайности для масштаба области, республики, страны в целом.

2. При равноускоренном (равнозамедленном) развитии явления во времени применяется полином 2–й степени (парабола): 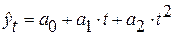. В этом случае постоянными являются вторые разности: 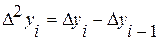. Такой характер развития возникает при наличии важных факторов прогрессивного развития (поступление нового высокопроизводительного оборудования, снятие ограничений в распределении дохода и пр.). Параметр 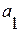выражает начальную скорость роста, коэффициент 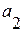– постоянную скорость изменения прироста (ускорение). Параболическая форма тренда с отрицательным ускорением ( 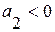) приводит со временем не только к приостановке роста уровня, но и к его снижению со всё большей скоростью. Такой характер развития свойственен производству устаревшей продукции.

3. Развитие явления с переменным ускорением (замедлением) описывается полином 3–й степени: 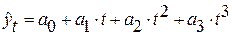. В данном случае постоянны третьи разности: 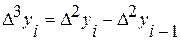, то есть абсолютные приросты ускоренно возрастают ( 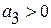) или замедляются ( ).

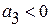4. Развитие явления, характеризующееся постоянным темпом роста (снижения), описывается показательной функцией: 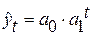(в частном случае – экспоненциальной функцией: 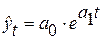). Величина 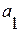( 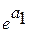) характеризует среднегодовой коэффициент роста 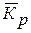. Если 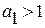, экспоненциальный (показательный) тренд выражает тенденцию ускоренного и все более ускоряющегося возрастания уровней динамического ряда. Такой характер свойственен размножению организмов при отсутствии ограничения со стороны среды: сорняков, вирусных заболеваний. При росте по экспоненте абсолютный прирост пропорционален достигнутому уровню. Однако, такой рост может продолжаться только небольшой исторический период, так как любой процесс развития всегда встретит ограничения.

При 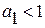, экспоненциальный (показательный) тренд означает тенденцию все более замедляющегося снижения уровней ряда. Такая тенденция присуща динамике трудоёмкости продукции, удельных затрат топлива или металла на единицу полезного эффекта (на 1 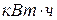, на 1 жилой площади и т.д.) при технологическом процессе.

5. При развитии явления с замедлением роста в конце периода применяется логарифмическая функция: 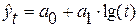. Логарифми-ческий тренд используется для отображения тенденции замедляющегося роста уровней при отсутствии предельного значения. Замедление роста становится все меньше и меньше, и при достаточно большом значении t логарифмическая кривая становится мало отличимой от прямой линии. Такая тенденция присуща росту спортивных достижений (чем они выше, тем труднее их улучшить), росту производительности аппарата по мере его совершенствования без качественных преобразований.

6. Гиперболическая форма тренда имеет вид: 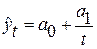. Если 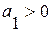, то гиперболический тренд соответствует тенденции замедляющегося снижения уровня, стремящегося к пределу 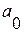. Если 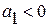, тренд выражает тенденцию замедляющегося роста уровней, стремящихся в пределе к 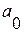. Следовательно, данная форма тренда используется для отображения процессов, ограниченных предельным значением уровня (предельным коэффициентом полезного действия двигателя, пределом 100 %-ной грамотности населения и т.п.).

Во-вторых, выбор типа модели должен быть основан на анализе графического изображения уровней динамического ряда (линейной диаграммы).

Методика измерения параметров тренда

Когда тип тренда установлен, вычисляют оптимальные значения параметров тренда, исходя из фактических уровней. Для этого обычно используют метод наименьших квадратов (МНК). В этом методе минимизируется сумма квадратов отклонений фактических уровней динамического ряда от выровненных уровней 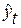(от тренда). Для каждого типа тренда МНК дает систему нормальных уравнений, решая которую, рассчитывают параметры тренда. Однако вычис-лительный процесс определения параметров тренда при сохранении полной идентичности конечных результатов может быть упрощен, если ввести обозначения дат (периодов) таким образом, чтобы .

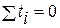Если количество уровней в ряду динамики нечетное, то временные даты (t) обозначаются следующим образом (табл. 7.1):

Таблица 7.1

Условное обозначение времени при нечетном числе уровней

Временные даты (периоды)
Уровни ряда динамики,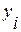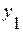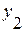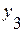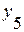
Обозначения временных дат, t	–2	–1

Если количество уровней в ряду динамики четное, то счет ведется полугодиями и обозначения временных дат (t) принимают следующий вид (табл. 7.2):

Таблица 7.2

Условное обозначение времени при четном числе уровней

Временные даты (периоды)
Уровни ряда динамики,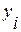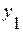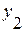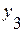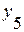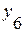
Обозначения временных дат, t	-5	-3	-1

В таблице 7.3 приводятся различные виды трендовых моделей и системы нормальных уравнений для определения параметров тренда.