Описание экспериментальной установки. Схема установки изображена на рис
Схема установки изображена на рис. 2.
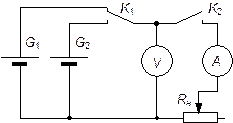
Рис. 2. Схема установки.
В качестве исследуемых источников G1 и G2 применяются щелочные аккумуляторы. Напряжение и ток измеряются вольтметром и амперметром постоянного тока. В качестве нагрузки используется магазин сопротивлений Rн .
Измерения и обработка результатов:
Собрать электрическую схему, показанную на рис. 2.
1. Переключателем K1 включить источник G1 и, не замыкая ключа K2, измерить вольтметром ЭДС (Е1) источника G1.
2. Затем ключом K2 подключить к источнику G1 нагрузку Rн и, изменяя сопротивление Rн от максимального до наименьшего значения (не менее 10 точек), измерить ток I и напряжение Uн. Замечание: во избежание сильного нагревания источника ЭДС, измерения при малых сопротивлениях Rн производить быстро.
3. Записать результаты измерений в таблицу 1.
Таблица 1
| Е В | № п\п | Rн, Ом | I А | Uн В | Р, Вт | Рн, Вт | h | Rн/Ri |
4. Переключателем K1 включить источник G2 и повторить измерения для него согласно п.п. 1-3.
5. Вычислить для каждого значения тока I и напряжения Uн полную мощность Р, полезную мощность Рн, КПД h и отношение Rн/Ri = Uн/(E – Uн) для обоих источников.
6. Построить графики следующих функций:
Pн = f(Rн/Ri), P = f(Rн/Ri), h = f(Rн/Ri) и Pн = f(I).
7. По полученным данным определить для каждого источника мощность короткого замыкания Pк.з. и внутреннее сопротивление источника Ri.
8. Провести математическую обработку результатов измерений, определить погрешности прямых и косвенных измерений и доверительную вероятность.
9. Записать значения Рк.з и Ri в стандартной форме.
КОНТРОЛЬНЫЕ ЗАДАНИЯ И ВОПРОСЫ
1. Записать основные характеристики постоянного электрического тока.
2. Записать закон Ома в дифференциальной форме.
3. Что такое электродвижущая сила?
4. Принцип действия химических источников ЭДС.
5. Чем отличается ЭДС от напряжения на клеммах источника энергии?
6. Как определить полезную и полную мощность источника ЭДС?
7. Доказать, что максимальная полезная мощность соответствует равенству Rн = Ri.
Лабораторная работа № 13
ИЗУЧЕНИЕ ЭФФЕКТА Холла
Цель работы: ознакомиться с явлением Холла и методикой измерения, измерить э.д.с. Холла, определить холловскую константу и концентрацию электронов в образце.
Приборы и принадлежности: датчик Холла, электромагнит, измерительные приборы, осциллограф, генератор, соединительные провода.
КРАТКАЯ ТЕОРИЯ
Электропроводность металлов зависит от концентрации электронов проводимости n и от их подвижности b. Обе эти величины, являющиеся важными характеристиками металла, могут быть определены из опыта.
Для измерения концентрации электронов чаще всего пользуются явлением Холла. Рассмотрим проводник в виде прямоугольной пластины, в которой течет ток с плотностью j(рис.1а).
Рис.1. Возникновение поперечной разности потенциалов в проводнике с током j под действием поперечного магнитного поля с индукцией B.
Эквипотенциальными поверхностями внутри такой пластинки будут плоскости, перпендикулярные к направлению тока, и поэтому разность потенциалов между двумя металлическими зондами 1 и 2, лежащими в одной из этих плоскостей, будет равна нулю.
Если поместить образец в магнитное поле B, перпендикулярное току и зондам (рис.1б), то между зондами возникнет разность потенциалов (э.д.с. Холлла), указывающая на то, что при наличии магнитного поля эквипотенциальные плоскости в пластинке становятся наклонными.
Явление Холла просто объясняется электронной теорией и является следствием существования силы Лоренца. Чтобы понять физическую сущность этого явления, ограничимся упрощенной его теорией и будем приближенно считать, что все электроны движутся с постоянной скоростью, равной средней скорости их упорядоченного движения v. Тогда на каждый электрон действует сила Лоренца, перпендикулярная направлению тока и магнитному полю:
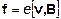, (1)
где е – заряд электрона.
Под действием этой силы электроны будут смещаться, так что одна из граней пластинки зарядится отрицательно, а другая - положительно, и внутри пластинки возникает поперечное электрическое поле E. При равновесии сила, действующая на электроны со стороны электрического поля, равна силе Лоренца:
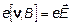(2)
Если толщина пластин d, холловская разность потенциалов их будет:
.
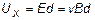Среднюю скорость электронов v можно выразить через плотность тока j, так как j = nev, и получим:
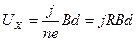, (3)
где R =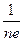 
- называют постоянной Холла. Постоянная Холла зависит от концентрации электронов n, и поэтому, измеряя постоянную Холла, можно определить концентрацию электронов внутри проводника или полупроводника.
Легко также видеть, что знак поперечной разности потенциалов зависит от знака заряда подвижных частиц, обуславливающих электропроводность. Действительно, пусть в проводящей пластине ток течет слева направо (рис.2а). Если подвижные частицы в проводнике несут положительный заряд, то скорость этих частиц имеет то же направление, что и ток, и при указанном направлении магнитного поля сила Лоренца будет направлена снизу вверх. В этом случае верхняя грань пластины будет заряжаться положительно, а нижняя - отрицательно.
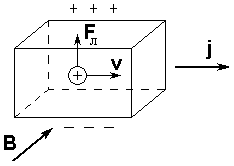
Рис.2а.
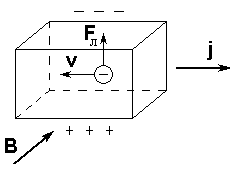
Рис.2б.
Если же частицы заряжены отрицательно, то их скорость направлена противоположно току (рис.2б). Так как сила Лоренца зависит и от заряда частиц, и от их скорости, то ее направление не изменится, и поэтому заряженные частицы так же будут накапливаться у верхней грани. Однако, так как частицы заряжены отрицательно, верхняя грань будет заряжаться отрицательно, а нижняя - положительно, т.о. э.д.с. Холла будет иметь обратный знак. Измеряя э.д.с. Холла UХ, индукцию магнитного поля B, в котором находится образец, силу тока I в образце и, зная ширину образца а, можно определить знак основных носителей заряда, постоянную Холла R и вычислить концентрацию носителей зарядов n.
Действительно, пользуясь соотношением (3) и учитывая, что плотность тока j = I/S, где S = ad - площадь поперечного сечения образца, можно найти постоянную Холла:
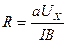. (4)
Так как R = 1/(ne), получим:
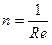. (5)
Зная же удельную электропроводность l = enb, можно найти произведение nb и, следовательно, определить подвижность b носителей заряда.
ПРАКТИЧЕСКАЯ ЧАСТЬ