Тізбектерге арифметикалық амалдар қолдану
Егер екі функцияның анықталу жиыны бірдей болып, ал мәндерінің жиынында арифметикалық амалдар анықталса, онда осы екі функцияға арифметикалық амалдар қолдануға болады.
{xn} және {уп} тізбектері берілсін. Осы тізбектер арқылы төмендегідей сәйкестікті көрсетуге болады:
n ® c × x n, яғни n санына схп саны сәйкес келеді.
n ® x n + y n, яғни n санына хn+ уn саны сәйкес келеді.
n ® x n - y n, яғни n санына хn - уn саны сәйкес келеді.
n ® x n × y n, яғни n санына хn • уn саны сәйкес келеді.
n ® x n /y n, яғни n санына хn / уn саны сәйкес келеді.
Арифметикалық амалдар мен тізбектердің шектері арасындағы байланысты зерттейік.
Теорема. {хn}, {уn} тізбектері берілсін және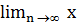 
n = а, 
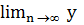n =b . Онда
a)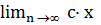 
n = c× a кез келген с нақты саны үшін
b)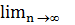 
(x +y )= а +b
c)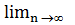 
(x n- y n ) = а - b
d) 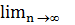x n ×y n =а × b
e) 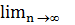x n / y n= а /b (мұндағы y n ¹ 0 (n= 1, 2, ...) және b ¹ 0 ).
Теорема. Егер тізбектің шегі нольге тең болса, ал {уn} тізбегі шектелген болса, онда {хn • уn} тізбегінің шегі бар және нольге тең.
ІІІ.Монотонды тізбектер
Монотонды тізбектердің анықтамасы.Негізгі теорема.
Анықтама. {хn} тізбегі берілсін. Егер кез келген n (n = 1,2,...) үшін x n £ x n+1 орындалса, онда тізбекті кемімейтін, ал x n < x n+1 - болса, оны өспелі тізбек деп атайды. Егер кез келген n (n = 1, 2,... ) үшін x n ³ x n+1 орындалса, онда тізбекті өспейтін, ал x n > x n+1 болса, оны кемімелі тізбек деп атайды. Осы тізбектердің барлығы монотонды тізбектер деп аталады. Өспелі және кемімелі тізбектер қатаң монотонды тізбектер деп аталады.
Мысалдар: 1°. xn - 
= өспелі шенелген тізбек.
xn
0 1 
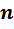
-1
2°.xn 
= 
- өспелі шенелмеген тізбек.
xn
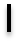
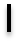
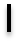
0 1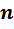
-1
3°. x n =( -1 ) n ×n - тізбегі шенелмеген, шегі жоқ, монотонды емес тізбек.
xn
40. x n =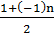 
тізбегі шенелген, шегі жоқ, монотонды емес тізбек.
. . .
х3 х4
х1 х2
0 1 Х
5°. x n =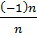 
шенелген,жинақталған, монотонды емес тізбек.
xn
1 
-1
Теорема. {хn} тізбегі монотонды болсын. Онда оның шегі бар (ақырлы әлде ақырсыз) және {хn} кемімейтін болғанда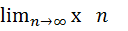 
= sup{x1 ; x2 ;...}, ал {хn} өспейтін болғанда 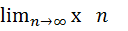inf {x1 ; x2 ;...}.
Дәлелдеуі. {хn} тізбегі кемімейтін тізбек болсын. Онда төмендегі шарттың тек біреуі орындалады, sup{x1 ; x2 ;...} º а - нақты сан (тізбектің мәндері жоғарыдан шенелген). sup{x1 ; x2 ;...} = +¥ (тізбектің мәндері жоғарыдан шенелмеген ).
1-жағдай. Оң e саны берілсін. Супремум анықтамасы бойынша:
1)а саны {х1,; х2;...} жиынының жоғарғы шекарасы, яғни барлық n үшін x n £ а болады;
2 ) а - e саны (х1,; х2;...} жиынының жоғарғы шекарасы емес, яғни x n e > a -e теңсіздігі орындалатын тізбектің x n e мүшесі табылады.
х1 х2 . . . x n e . . . . . . . . . хn
а - e а а+e
{хn} тізбегі барлық n ³ ne үшін кемімейтін тізбек болғандықтан; x n ³ x n e теңсіздігі орындалады. Қорытындылай келе, мынаған келеміз: Әрбір n > nе үшін a -e < x n e £ xn £ a < a +e , теңсіздігі орындалады, ал бұл,
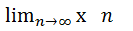= sup{x1 ; x2 ;...}, мынадай символмен жазылады.
2-жағдай. Оң e саны берілсін. Онда тізбектің одан үлкен мүшесі яғни n e номері үшін мына теңсіздікті x n e >e қанағаттандыратындай табылады.
Енді тізбек кемімейтін деп есептеп, барлық n > ne үшін xn ³ xne > e теңсіздігі орындалады делік, сондықтан шектің анықтамасы бойынша 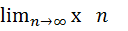= sup{x1 ; x2 ;...},. Теорема дәлелденді.
Өспейтін тізбек үшін де теорема осы бағытта дәлелденеді.