Відношення. Властивості відношень

1. Нехай M = {1,2,3,4,5}. Для заданого відношення R на множині M визначити Pr₁R, Pr₂R, R ^-1, R °R, R °R ^-1, R ^-1°R і R⁽³⁾:

(а) R = {(1,2),(1,4),(2,3),(2,4),(4,1),(4,3),(4,4)};

(б) R = {(1,2),(2,3),(3,5),(4,1),(5,4)};

(в) R = {(2,4),(2,5),(3,1),(3,2),(3,3),(5,2)};

(г) R = {(1,1),(2,2),(3,3),(4,2),(4,3),(5,1),(5,5)}.

2. Для заданого відношення R на множині N

(а) R = { (m,n) | m ділиться на n };

(б) R = { (m,n) | n ділиться на m };

(в) R = { (m,n) | m - n ділиться на k, kÎN };

(г) R = { (m,n) | m < n }

визначити Pr₁R, Pr₂R, R ^-1, R °R, R °R ^-1, R ^-1°R, .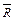

3. Відношення R на множині N натуральних чисел задано рекурентно

1) (1,1)ÎR; 2) якщо (m,n)ÎR, то (m+1,n)ÎR і (m,n+1)ÎR.

Довести, що R = N´N.

4. Відношення R на множині N натуральних чисел задано рекурентно

1) (1,1)ÎR;

2) якщо (m,n)ÎR, то (m+1,n)ÎR, (m+1,n+1)ÎR і (m+1,n+2)ÎR.

Описати відношення R.

5. Нехай на множині всіх людей P означені відношення:

F = {(x,y) ½ x,yÎP і x є батьком y };

D = {(x,y) ½ x,yÎP і x є донькою y }.

Описати такі відношення:

(а) F°F; (г) D°F; (є) F^-1°D^-1;

(б) D°D; (д) D°F^-1; (ж) D^-1°F;

(в) F°D; (е) F^-1°D; (з) D^-1°D^-1.

6. На множині M = {1,2,3,4} задано відношення

R₁ = {(1,1),(1,3),(2,3),(2,4),(3,1),(3,3),(4,1)},

R₂ = {(1,2),(1,3),(1,4),(2,2),(3,1),(3,4),(4,2)}.

Знайти відношення X на множині M (або довести, що таке відношення X не існує), для якого виконується

(а) R₁°X = R₂; (в) R₂°X = R₁; (д) (R₁°R₂)°X = R₁;

(б) X°R₁ = R₂; (г) X°R₂ = R₁; (е) (R₂°R₁)°X = R₁.

7. На множині M = {1,2,3,4} задано відношення R = {(1,1),(1,2),(2,3),(3,3),(3,4),(4,4)}. Знайти такі два відношення T і S на M, що T¹S і R°T = R°S = {(1,1),(1,2),(1,4)}.

8. Довести, що для довільного відношення R на множині M виконується

(а) Pr₁R = Æ Û R = Æ Û Pr₂R = Æ;

(б) Pr₂R = Pr₁R ^-1;

(в) Pr₁R = Pr₂R ^-1;

(г) Pr₁R=M Û i_M Í R°R^-1;

(д) Pr₂R=M Û i_M Í R^-1°R.

9. Довести, що для будь-яких відношень виконується

(а) R È R = R Ç R = R; (д) (R₁ \ R₂)^-1 = R₁^-1 \ R₂^-1;

(б) (R ^-1)^-1 = R; (е) 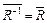^-1;

(в) (R₁ÈR₂)^-1 = R₁^-1ÈR₂^-1; (є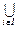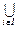) ( R_i)^-1 = R_i^-1;

(г) (R₁ÇR₂)^-1 = R₁^-1ÇR₂^-1; (ж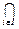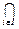) ( R_i)^-1 = R_i^-1.

10. Довести, що для довільних відношень виконується

(а) R₁° (R₂°R₃) = (R₁°R₂)°R₃;

(б) (R₁°R₂)^-1 = R₂^-1°R₁^-1;

(в) ( 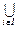R_i)°Q = 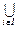(R_i °Q) ;

(г) Q ° ( 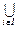R_i) = 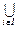(Q °R_i);

(д) R₁°R₂ = Æ Û Pr₂R₁ÇPr₁R₂ = Æ.

11. Довести, що для довільних відношень R_i, iÎI та Q на множині M

(а) ( 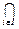R_i)°Q Í 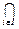(R_i°Q) ; (б) Q ° ( 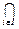R_i) Í 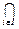(Q °R_i)

і знак включення не можна замінити на знак рівності.

12. Навести приклад відношень R₁ і R₂ на множині M = {1,2,3} таких, що відношення R₁°R₂ і R₂°R₁ не збігаються.

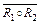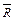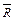13. Нехай R₁ і R₂ - відношення на множині M. Довести або спростувати таку рівність: = ₁° ₂.

14. Знайти всі відношення X на множині M такі, що для довільного відношення R на M виконується рівність R°X = X°R.

15. Нехай R - відношення на множині M. Довести, що R°R₁=R₁°R=R₁ для довільного відношення R₁ на множині M тоді і тільки тоді, коли R=i_M .

16. Довести, що співвідношення R°H=H°R=H виконується для довільного відношення R тоді і тільки тоді, коли H= Æ.

17. Для яких відношень виконується R ^-1 = ?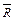

18. Довести, що коли R₁ÍR₂, тоді для довільного відношення Q виконується

(а) Q °R₁ Í Q °R₂; (б) R₁°Q Í R₂°Q; (в) R₁^-1Í R₂^-1.

19. На множині M = {1,2,3,4} задано відношення

R₁ = {(1,1),(1,3),(2,2),(2,4),(3,1),(3,3),(4,2),(4,4)};

R₂ = {(1,1),(2,2),(2,3),(2,4),(3,1),(3,3),(4,1),(4,4)};

R₃ = {(1,3),(1,4),(2,1),(1,2),(3,1),(3,3),(4,1)};

R₄ = {(1,1),(1,2),(1,4),(2,2),(2,4),(3,3),(3,4),(4,2),(4,3),(4,4)};

R₅ = {(1,2),(1,3),(2,3),(2,4),(4,1),(4,3)}.

Визначити, які з цих відношень є

(а) рефлексивними;

(б) антирефлексивними;

(в) симетричними;

(г) антисиметричними;

(д) транзитивними.

Побудувати графіки, графи та матриці заданих відношень.

20. Дайте інтерпретацію властивостей відношень за допомогою їхніх матриць, графіків і діаграм.

21.На множині Z задано відношення:

(m,n)ÎR₁Û m-n парне число;

(m,n)ÎR₂Û m+n парне число;

(m,n)ÎR₃Û m-n £ 100;

(m,n)ÎR₄Û m-n непарне число;

(m,n)ÎR₅Û m+n непарне число;

(m,n)ÎR₆Û m/n парне число;

(m,n)ÎR₇Û m/n непарне число;

(m,n)ÎR₈Û m* n парне число;

(m,n)ÎR₉Û m* n непарне число;

(m,n)ÎR₁₀Û m-n є степенем числа 2;

(m,n)ÎR₁₁ Û m і n є взаємно простими;

(m,n)ÎR₁₂ Û m £ n;

(m,n)ÎR₁₃ Û m ділить n;

(m,n)ÎR₁₄ Û m / n є степенем числа 2.

Визначити, які з цих відношень є

(а) рефлексивними;

(б) антирефлексивними;

(в) симетричними;

(г) антисиметричними;

(д) транзитивними;

(е) толерантними.

22. Нехай R₁ і R₂ - деякі відношення на скінченній множині M, а C₁ і C₂ матриці цих відношень. Визначити матрицю C для відношення

(а) R₁ÈR₂; (г) R₁DR₂; (є) ;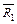

(б) R₁ÇR₂; (д) R₁°R₂; (ж) i_M ÈR₁;

(в) R₁\R₂; (е) R₁^-1; (з) R₁\ i_M.

23. Довести, що для довільних рефлексивних відношень R₁ і R₂ відношення R₁ÈR₂, R₁ÇR₂, R₁^-1 і R₁°R₂ будуть також рефлексивними.

24. Довести, що для довільного рефлексивного відношення R і для будь-якого k=0,1,2,... відношення R^(k) є рефлексивним.

25. Довести, що для довільних рефлексивних відношень R₁ і R₂ виконується R₁ÈR₂ÍR₁°R₂.

26. Нехай R - відношення на множині M. Довести або спростувати таке твердження: якщо R°R - рефлексивне, то і R рефлексивне.

27. Довести, що відношення R на множині M є рефлексивним тоді і лише тоді, коли

(а) i_M Í R; (б) i_M ÇR = i_M; (в) i_M ÈR = R.

28. Нехай R_i, iÎI - відношення на множині M. Довести або спростувати таке твердження:

(а) 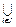R_i - рефлексивне тоді і тільки тоді, коли кожне R_i рефлексивне, iÎI;

(б) 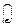R_i - рефлексивне тоді і тільки тоді, коли кожне R_i рефлексивне, iÎI;

(в) R_i°R_j - рефлексивне тоді і тільки тоді, коли R_i і R_j рефлексивні, i,jÎI;

(г) R_i^-1 - рефлексивне тоді і тільки тоді, коли R_i рефлексивне.

29. Нехай R - відношення на скінченній множині M (|M| = n). Довести або спростувати таке твердження:

(а) якщо R рефлексивне, то |R|³n;

(б) якщо |R|³n, то R рефлексивне.

30. Рефлексивним замиканням відношення R на множині M назвемо найменше рефлексивне відношення на M, яке містить R; позначимо його r(R).

Довести, що для довільного відношення R на множині M виконується

(а) r(R)=RÈi_M;

(б) якщо RÍR¢ і R¢ - рефлексивне, то r(R)ÍR¢.

31. Довести, що коли відношення R₁ і R₂ антирефлексивні, тоді антирефлексивними є і відношення R₁ÈR₂, R₁ÇR₂, R₁^-1.

32. Довести, що композиція R₁°R₂ двох антирефлексивних відношень R₁ і R₂ може не бути антирефлексивним відношенням.

33. Нехай R_i, iÎI - відношення на множині M. Довести або спростувати таке твердження:

(а) 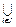R_i - антирефлексивне тоді і тільки тоді, коли кожне R_i антирефлексивне, iÎI;

(б) 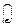R_i - антирефлексивне тоді і тільки тоді, коли кожне R_i антирефлексивне, iÎI;

(в) R_i°R_j - антирефлексивне тоді і тільки тоді, коли R_i і R_j антирефлексивні, i,jÎI;

(г) R_i^-1 - антирефлексивне тоді і тільки тоді, коли R_i антирефлексивне.

34. Навести приклад двох антирефлексивних відношень R₁ і R₂ на множині M = {1,2,3}, композиція R₁°R₂ яких буде рефлексивним відношенням.

35. Довести, що для симетричних відношень R₁і R₂ будуть симетричними і відношення R₁ÈR₂, R₁ÇR₂, R₁^-1, R₁°R₁^-1.

36. Довести, що для довільного симетричного відношення R і для будь-якого k=0,1,2,... відношення R^(k) є симетричним.

37. Довести, що відношення R є симетричним тоді і тільки тоді, коли

(а) R=R ^-1; (б) R^-1Í R; (в) R Í R^-1.

38. Симетричним замиканням відношення R на множині M назвемо найменше симетричне відношення на M, яке містить R; позначимо його s(R).

Довести, що для довільного відношення R на множині M виконується

(а) s(R)=RÈR^-1;

(б) якщо RÍR¢ і R¢ - симетричне, то s(R)ÍR¢.

39. Довести, що відношення R на множині M не є симетричним тоді і тільки тоді, коли RÇR^-1=Æ.

40. Довести, що для симетричного відношення R виконується Pr₁R=Pr₂R.

41. Спростувати таке твердження: якщо для деякого відношення R виконується Pr₁R = Pr₂R, то відношення R є симетричним.

42. Довести, що відношення R симетричне, тоді і тільки тоді, коли симетричним є відношення

(а) R^-1; (б) .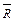

43. Побудувати два симетричних відношення R₁ і R₂на множині M={1,2,3,4}, композиція яких R₁°R₂не буде симетричним відношенням.

44. Нехай R₁ і R₂ - симетричні відношення на множині M. Довести, що коли R₁°R₂ÍR₂°R₁, то R₁°R₂ = R₂°R₁.

45. Довести, що композиція R₁°R₂ симетричних відношень R₁ і R₂ є симетричним відношенням тоді і тільки тоді, коли R₁°R₂ = R₂°R₁.

46. Довести, що композиція R₁°R₂ симетричних відношень R₁ і R₂ є симетричним відношенням тоді і тільки тоді, коли R₂°R₁ÍR₁°R₂ .

47. Нехай R_i, iÎI - відношення на множині M. Довести або спростувати таке твердження:

(а) 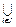R_i - симетричне тоді і тільки тоді, коли кожне R_i симетричне, iÎI;

(б) 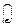R_i - симетричне тоді і тільки тоді, коли кожне R_i симетричне, iÎI;

(в) R_i°R_j - симетричне тоді і тільки тоді, коли R_i і R_j симетричні, i,jÎI;

(г) R_i^-1 - симетричне тоді і тільки тоді, коли R_i симетричне.

28. Довести, що для антисиметричних відношень R₁ і R₂ відношення R₁ÇR₂ і R₁^-1 будуть також антисиметричними.

48. Довести, що відношення R на множині M є антисиметричним тоді і тільки тоді, коли R ÇR ^-1Í i_M.

49. Довести, що об’єднання R₁ÈR₂ антисиметричних відношень R₁ і R₂ на множині M буде антисиметричним відношенням тоді і тільки тоді, коли R₁ÇR₂^-1Í i_M.

50. Нехай R_i, iÎI - відношення на множині M. Довести або спростувати таке твердження:

(а) 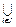R_i - антисиметричне тоді і тільки тоді, коли кожне R_i антисиметричне, iÎI;

(б) 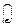R_i - антисиметричне тоді і тільки тоді, коли кожне R_i антисиметричне, iÎI;

(в) R_i°R_j - антисиметричне тоді і тільки тоді, коли R_i і R_j антисиметричні, i,jÎI;

(г) R_i^-1 - антисиметричне тоді і тільки тоді, коли R_i антисиметричне.

51. Нехай R - антисиметричне відношення на скінченній множині M (|M| = n). Яким є найбільше значення для величини |R|? Для скількох антисиметричних відношень R на M це найбільше значення досягається?

52. Довести, що відношення R на множині M є транзитивним тоді і тільки тоді, коли R °R Í R.

53.Довести, що рефлексивне відношення R є транзитивним тоді і тільки тоді, коли R°R = R.

54. Довести, що транзитивне і антирефлексивне відношення R є антисиметричним.

55. Довести, що відношення R транзитивне тоді і тільки тоді, коли відношення R^-1транзитивне.

56. Довести, що перетин транзитивних відношень є транзитивним відношенням.

57. Довести, що для довільного транзитивного відношення R і для будь-якого k=0,1,2,... відношення R^(k) є транзитивним.

58. Навести приклад транзитивних відношень R₁ і R₂ на множині M={1,2,3,4} таких, що

(а) R₁°R₂ - нетранзитивне; (г) R₁°R₁=R₁;

(б) R₁°R₂ - транзитивне; (д) R₁ÈR₂ - нетранзитивне;

(в) R₁°R₁¹R₁; (е) R₁ÈR₂ - транзитивне.

59. Довести, що композиція R₁°R₂ транзитивних відношень R₁ і R₂ є транзитивним відношенням, якщо R₁°R₂ = R₂°R₁.

60. Довести, що об’єднання R₁ÈR₂ транзитивних відношень R₁ і R₂ буде транзитивним відношенням тоді і тільки тоді, коли R₁°R₂ È R₂°R₁ Í R₁ÈR₂.

61. Нехай R_i, iÎI - відношення на множині M. Довести або спростувати таке твердження:

(а) 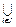R_i - транзитивне тоді і тільки тоді, коли кожне R_i транзитивне, iÎI;

(б) 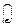R_i - транзитивне тоді і тільки тоді, коли кожне R_i транзитивне, iÎI;

(в) R_i°R_j - транзитивне тоді і тільки тоді, коли R_i і R_j транзитивні, i,jÎI;

(г) R_i^-1 - транзитивне тоді і тільки тоді, коли R_i транзитивне.

62. Довести, що для рефлексивного й транзитивного відношення R виконується R°R=R. Чи справедливе обернене твердження ?

63. Знайти помилку в наведених міркуваннях. Якщо R симетричне і транзитивне відношення на множині M, то R - рефлексивне, оскільки з того, що (a,b)ÎR послідовно випливає (b,a)ÎR і (a,a)ÎR.

64. Навести приклад відношення R на множині M = {1,2,3,4}, яке

(а) не є рефлексивним, але й не є антирефлексивним;

(б) не є симетричним, але й не є антисиметричним.

65. Побудувати відношення R на множині M = {1,2,3}, яке є симетричним і антисиметричним одночасно.

66. Побудувати відношення

(а) симетричне, транзитивне, нерефлексивне;

(б) рефлексивне, симетричне, нетранзитивне;

(в) рефлексивне, антисиметричне, нетранзитивне;

(г) рефлексивне, симетричне, транзитивне;

(д) рефлексивне, несиметричне, транзитивне;

(е) антисиметричне, транзитивне, нерефлексивне;

(є) несиметричне, неантисиметричне;

(ж) нерефлексивне, неантирефлексивне, несиметричне, транзитивне.