Основное уравнение динамики вращательного движения

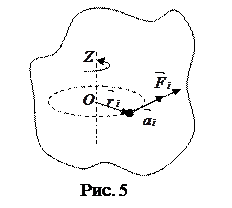Выберем произвольно некоторую точку с массой m_i , на которую действует сила 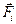, сообщая точке ускорение 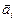(рис. 5). Поскольку вращение создает только тангенциальная составляющая, для упрощения вывода 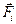направлена перпендикулярно оси вращения.

В этом случае .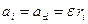

Согласно второму закону Ньютона 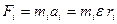. Умножим обе части равенства на r_i:

,

,

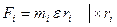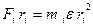где 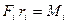- момент силы, действующей на материальную точку,

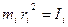- момент инерции материальной точки.

Следовательно, .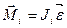

Для всего тела: , ,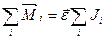

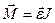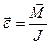, (1)

т.е. угловое ускорение тела прямо пропорционально моменту действующих на него внешних сил и обратно пропорционально его моменту инерции. Уравнение (1) представляет собой уравнение динамики вращательного движения твердого тела относительно неподвижной оси, или второй закон Ньютона для вращательного движения.