Возможные и виртуальные перемещения

Перемещение материальной точки зависит от ее массы, приложенных к точке сил связей и начальных условий. Определение перемещения точки сводится к решению задачи динамики точки. В аналитической механике используются два основных понятия о возможном и виртуальном перемещениях точки.

Пусть на материальную точку наложена голономная нестационарная удерживающая связь, уравнение которой

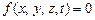. (2.4)

Возможнымперемещением несвободной материальной точки называется такое бесконечно малое перемещение, отвечающее бесконечно малому промежутку времениdt,которое допускается наложенными на систему ограничениями – связями,
обозначается d 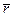(dx,dy,dz)(рис. 2.5). Этому уравнению удовлетворяют координаты точки М в момент времени t. Через
бесконечно малый промежуток времени dt координаты 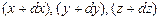точки также должны удовлетворять уравнению связи:

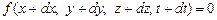. (2.5)

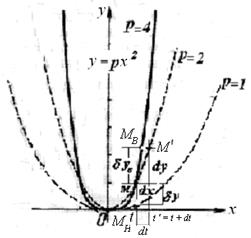
Рис. 2.5

Раскладывая функцию (2.5) в ряд Тейлора с точностью до слагаемых выше первого порядка малости и учитывая, что связь имеет вид (2.4), получаем

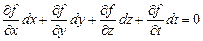. (2.6)

Выражение (2.6) представляет собой условие, которому должны удовлетворять проекции вектора d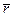элементарного возможного перемещения точки.

Виртуальнымперемещением несвободной материальной точки, отвечающим данному моменту времени t, называется такое воображаемое, бесконечно малое, прямолинейное, соответствующее данному моменту времени t перемещение точки, которое могло бы иметь место, если начиная с этого момента времени связи, наложенные на ее движение, сделались бы неизменяемыми.

Виртуальныеперемещения точки обозначаются вариациями: вектор 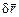называют вариацией радиуса-вектора точки,а проекции на оси декартовой системы координат - вариациями координат dx,dy,dz .

Виртуальныеперемещения не связаны ни с движением точки, ни с изменением наложенных связей. Они представляют собой воображаемые перемещения, которые можно представить совокупностью бесконечно малых векторов 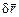,зависящих только от структуры связей, зафиксированных в данный момент времени.Виртуальныеперемещения точки должны удовлетворять дифференциальным соотношениям, вытекающим из уравнений связей при условии, что время является фиксированным. Получим эти соотношения и установим различие между бесконечно малым возможным 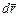ивиртуальным 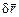перемещениями точки.

Пример 2.5.Представим теперь (см. рис. 2.5), что перемещение точки из положения, занимаемого ею в данный момент времени, в бесконечно близкое происходит в результате изменения координат точки при фиксированном времени t (т.е. либо вертикально вверх (р=4), либо вертикально вниз (р=1), функция (парабола y = p x², p=2 ) как бы изменяется не за счет аргумента, а за счет параметра р).

Координаты точки с учетом их вариации должны удовлетворять уравнению связи

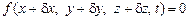. (2.7)

Раскладывая эту функцию в ряд Тейлора с точностью до слагаемых выше первого порядка малости и учитывая, что связь имеет вид (2.4), получаем

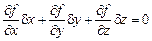. (2.8)

Таким образом, при наличии связи вида (2.4) вариации координат точки должны удовлетворять условию (2.8), при выводе которого время полагалось фиксированным. Поэтому данное условие должно выполняться как при стационарных, так и при нестационарных связях, наложенных на точку.

Используя понятие вектора-градиента, выражение (2.8) можно рассматривать как скалярное произведение векторов :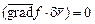

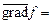
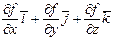(2.9)

и

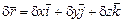. (2.10)

Вектор-градиент расположен вдоль главной нормали к поверхности 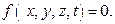Поэтому условие (2.8) означает что вектор 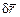ортогонален главной нормали и, следовательно, расположен по касательной. Поэтому при исследовании несвободного движения точки, системы точек или системы тел удобно пользоваться образом касательного пространства. В качестве примера рассмотрим движение материальной точки по гладкой плоской кривой, пусть это будет уравнение параболы y = p x² (рис. 2.5), где p=2. Положение материальной точки М определяется ее координатами (x, y). Однако y = ƒ(x) и, следовательно, положение точки М полностью задается только величиной x. Пусть за промежуток времени dt точка М переместится и займет положение М' с координатами (x+dx), (y+dy).

Так как по определению,виртуальным перемещением несвободной точки, отвечающим фиксированному моменту времени t, называется такое воображаемое, бесконечно малое, прямолинейное, соответствующее данному моменту времени перемещение точки, которое могло бы иметь место, если начиная с этого момента времени связи, наложенные на ее движение, сделались бы неизменяемыми, то в данном случае точка М может переместиться только вертикально либо вверх в положение М_в, либо вниз – в положение М_н. Это значит, что изменение функции в данный момент времени t произошло не за счет аргумента x, а за счет параметра p, пусть p=4 или p=1. Это и будет виртуальным перемещением точки dy, отвечающим функции y = p·x² (рис. 2.5), где p=2.

В дальнейшем условимся применять краткое выражение:
«даем системе виртуальное перемещение».

С точки зрения математики, виртуальные перемещения – это изохронные вариации координат точек, подчиненные уравнениям связи.

Так как слово «перемещение» ассоциируется с «передвижением», то, может быть, для понимания существа метода вместо термина «виртуальные перемещения» следует употреблять термин «изохронные вариации» - ведь когда мы сообщаем виртуальное перемещение, в действительности никакого передвижения не происходит.

Поэтому криволинейные перемещения точек заменяют прямолинейными отрезками, отложенными по касательным к траекториям точек.

Установим связь между элементарными возможными и виртуальными перемещениями точек.

Если наложенная на точку связь стационарная, то 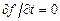и условие (2.6) аналогично условию (2.8). Следовательно, если связь стационарная, то элементарное возможное перемещение точки совпадает с одним из виртуальных.

При нестационарной связи условие (2.6) для проекций вектора d 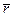не совпадает с условием (2.8) для проекций вектора 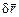. Поэтомувозможное перемещение точки в этом случае не принадлежит к числу виртуальных. Вариации определяются так же, как и дифференциалы.

Пример 2.6.Математический маятник (рис. 2.3). Точка О – цилиндрический шарнир, ОМ= l – невесомый нерастяжимый стержень. Уравнения связей удерживающих (двусторонних), голономных стационарных: 1) z = 0, 2) x² + y² – l ² = 0.

Координаты точки М: x = l cos (j), y = l sin (j).

Их вариации dx = - l sin (j) dj, dy = l cos (j) dj .

Виртуальное перемещение 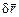направлено по касательной к окружности.

Пример 2.7.Если ОМ = l (t), (рис. 2.4), то уравнения связей будут иметь вид: 1) z = 0 , 2) x² + y² – l (t) ² £ 0. Связи неудерживающие (односторонние), голономные, нестационарные. Координаты точки М: x = l (t) cos (j), y = l (t) sin (j). Их вариации
dx = - l (t)sin (j) dj, dy = l (t) cos (j) dj , т.е. согласно определению виртуальных перемещений мы забываем, что l (t) –переменная от времени и полагаем, что l (t) соответствует фиксированному моменту времени.