Общее решение однородной линейной системы
Рассмотрим однородную линейную систему
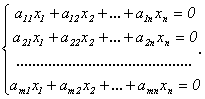 . (4.2)
. (4.2)
Отметим, что такая система всегда совместна, поскольку имеет нулевое решение 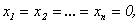 называемое тривиальным.
называемое тривиальным.
Пусть ранг матрицы системы r<n. Предположим, что в базисный минор входят коэффициенты первых r уравнений. Тогда оставшиеся m – rуравнений являются линейными комбинациями, то есть следствиями предыдущих. Поэтому можно оставить в системе только первые r уравнений:
. 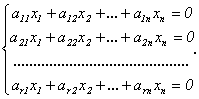
Оставим в левой части каждого уравнения неизвестные, коэффициенты при которых входят в базисный минор, а остальные неизвестные перенесем направо:
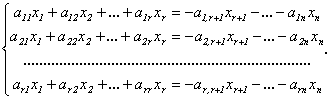 (4.3)
(4.3)
Эта система будет иметь единственное решение относительно неизвестных 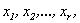 выражающее их через остальные неизвестные (
выражающее их через остальные неизвестные ( 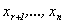 ), которым можно придавать любые произвольные значения. Таким образом, система (4.2) при r<n является неопределенной.
), которым можно придавать любые произвольные значения. Таким образом, система (4.2) при r<n является неопределенной.
Определение 4.7. Неизвестные 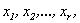 коэффициенты при которых входят в базисный минор матрицы системы, называются базисными неизвестными, а остальные (
коэффициенты при которых входят в базисный минор матрицы системы, называются базисными неизвестными, а остальные ( 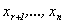 ) – свободными неизвестными.
) – свободными неизвестными.
Определение 4.8. Решения системы (4.2) 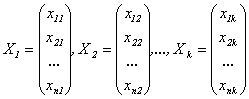 (4.4) называются линейно независимыми, если линейная комбинация
(4.4) называются линейно независимыми, если линейная комбинация 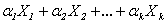 дает нулевой столбец только при
дает нулевой столбец только при 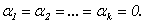
Покажем, что число линейно независимых решений системы (4.2) равно n – r. Действительно, рассмотрим столбцы вида
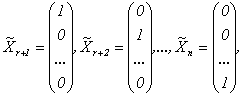 (4.5) содержащие по n-r чисел. Очевидно, что эти столбцы линейно независимы, а любой другой столбец той же размерности является их линейной комбинацией. Пусть эти столбцы задают значения свободных неизвестных системы (4.2).
(4.5) содержащие по n-r чисел. Очевидно, что эти столбцы линейно независимы, а любой другой столбец той же размерности является их линейной комбинацией. Пусть эти столбцы задают значения свободных неизвестных системы (4.2).
Тогда базисные неизвестные будут однозначно определяться для выбранных свободных неизвестных из системы (4.3) по правилу Крамера, и все решения системы, соответствующие наборам свободных неизвестных (4.5), образуют n-r линейно независимых столбцов вида (4.4), то есть n-rлинейно независимых решений системы (4.2).
Определение 4.9. Любые n – r линейно независимых решений системы (4.2) называются ее фундаментальной системой решений.
Определение 4.10. Фундаментальная система решений линейной однородной системы, в которой свободные неизвестные задаются по формулам (4.5), называется нормальной фундаментальной системой решений.
Замечание. Очевидным образом доказываются свойства решений однородной линейной системы (4.2):
Свойство 1. Сумма решений системы (4.2) является ее решением.
Свойство 2. Столбец решений (4.2), умноженный на любое число, тоже есть решение этой системы.
Следовательно, любая линейная комбинация фундаментальной системы решений системы (4.2) является ее решением. Можно доказать и обратное утверждение:
Теорема 4.3(без доказательства). Любое решение однородной линейной системы (4.2) является линейной комбинацией фундаментальной системы ее решений.
Таким образом, любое решение системы (4.2) имеет вид:
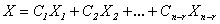 , где
, где 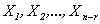 - фундаментальная система решений.
- фундаментальная система решений.
Пример.
Решим систему 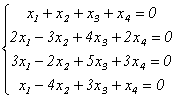 . Найдем ранг матрицы системы
. Найдем ранг матрицы системы 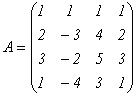 . Преобразуем ее к виду:
. Преобразуем ее к виду: 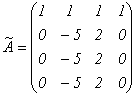 . Очевидно, что r(A)=2.
. Очевидно, что r(A)=2.
Пусть 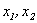 - базисные неизвестные,
- базисные неизвестные, 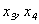 - свободные неизвестные. Заменим исходную систему системой из первых двух уравнений, коэффициенты которых входят в базисный минор, и перенесем базисные неизвестные в правые части уравнений:
- свободные неизвестные. Заменим исходную систему системой из первых двух уравнений, коэффициенты которых входят в базисный минор, и перенесем базисные неизвестные в правые части уравнений:
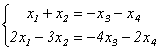 . Пусть
. Пусть 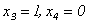 . Тогда
. Тогда 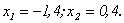 Если
Если 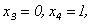
то 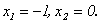 Получена фундаментальная система решений:
Получена фундаментальная система решений: 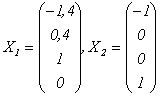 .
.
Теперь общее решение системы можно записать в виде: 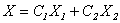 , где С1 и С2 – любые произвольные числа.
, где С1 и С2 – любые произвольные числа.
