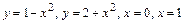Для функции найтиточки разрыва функции и исследовать их характер.Построить график функции.

Решение.

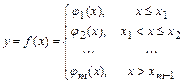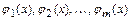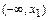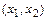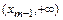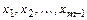Точками разрыва функции являются точки разрыва функций в промежутках , ,…, , кроме того, точками возможного разрыва функции являются точки в окрестности которых и в самих точках функция задаётся разными аналитическими выражениями.

Точка 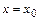является точкой непрерывности функции тогда и только тогда, когда: .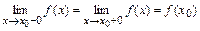

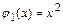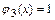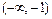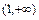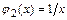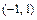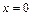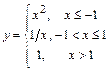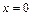Функции и непрерывны в промежутках и как элементарные функции, определённые в каждой точке данных промежутков, а функция в промежутке имеет точкой разрыва точку , в которой она не определена. Тогда для функции точка является точкой разрыва, а точк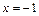и и 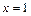, в окрестности которых и в самих точках функция задаётся разными аналитическими выражениями, являются точками возможного разрыва.

Исследуем на разрыв точки 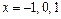и установим характер разрыва:

1)

.

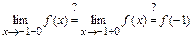
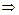
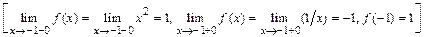
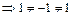Следовательно, точка 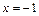- точка разрыва 1-го рода функции .

2)

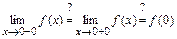
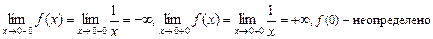. Следовательно, точка 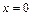- точка бесконечного разрыва (2-го рода) функции .

3)

.

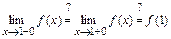
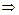
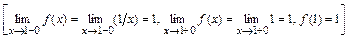
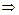
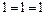Следовательно, точка 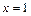- точка непрерывности функции .

График функции 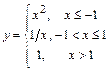имеет вид, изображённый на рисунке:

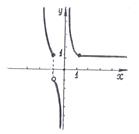
Ответ: 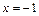- точка разрыва 1-го рода, 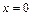-точка бесконечного разрыва.

61-70.Найти производную :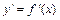

А) б) в) ; г) .

Нахождение производной 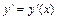функции 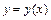заданной явно, с помощью правил дифференцирования:

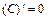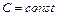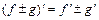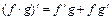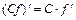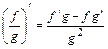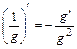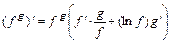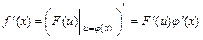( ), , , , , , , сводят к нахождению табличных производных (приложение 6.3).

Решение.

а)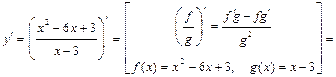

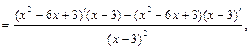где

,

.

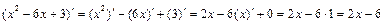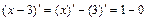Тогда .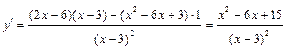

б) 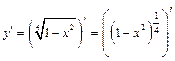. Представим функцию в виде сложной функции 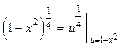и применим правило вычисления производной сложной функции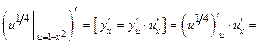

.

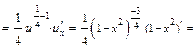
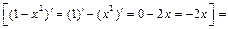
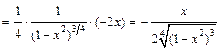в) 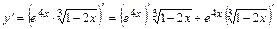, где

= ;

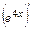
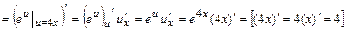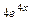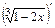
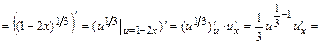
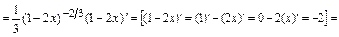
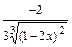
Тогда .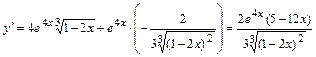

г) 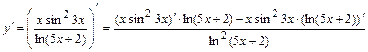,где

.

.

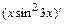
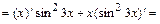
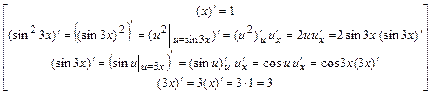
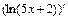
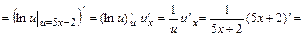
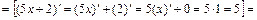
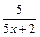Тогда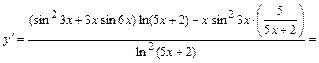

.

71-80.Вычислить пределы:

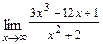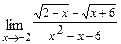а) б) в)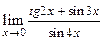

Вычисление предела 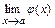, где 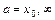, начинают всегда с подстановки в 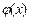предельного значения её аргумента 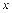. В результате могут получиться неопределённости 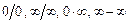,…, которые раскрывают или тождественными преобразованиями 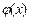такими, чтобы преобразованное выражение получилось определённым, или применением правила Лопиталя.

При вычислении пределов без применения правила Лопиталя будем использовать свойства конечных пределов и бесконечно больших и малых функций, а также следующие известные пределы: , , , .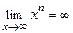

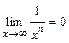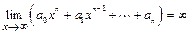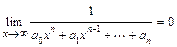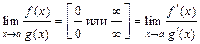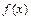Правило Лопиталя , где и 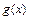- функции, дифференцируемые в окрестности 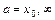, позволяет во многих случаях существенно упростить вычисление пределов. В некоторых случаях может потребоваться неоднократное применение данного правила. Перед очередным применением правила Лопиталя следует обязательно проверить, имеют ли место неопределённост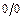и или 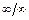, если – да, то данное правило можно применить ещё раз. На каждом этапе его применения следует использовать, упрощающие отношение тождественные преобразования, а также комбинировать это правило с любыми другими известными приёмами вычисления пределов.

Решение. а) 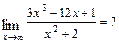При подстановке вместо переменной 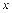её предельного значения 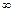получим неопределённость 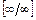. Для её раскрытия сначала разделим числитель и знаменатель дроби на 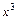(старшую степень переменной 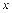в числителе и знаменателе), после чего используем свойства конечных пределов и бесконечно больших и малых функций. Получим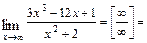

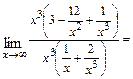
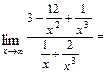
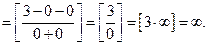
б) 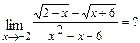При подстановке вместо переменной 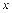её предельного значения 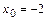получим неопределённость 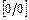. Для её раскрытия выделим в числителе и знаменателе дроби общий множитель вида 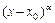, где 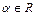- некоторое число, т.е. множитель 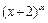. Затем сократим на него числитель и знаменатель дроби, после чего используем свойства пределов.

1) В квадратном трёхчлене 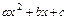множитель выделяют разложением квадратного трёхчлена по формул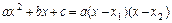е , где .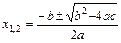

2) В выражении 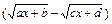множитель выделяют таким способом: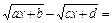

.

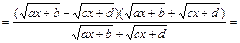
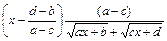В результате получим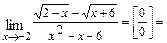

.

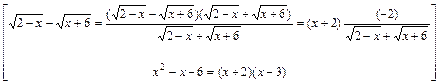
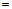
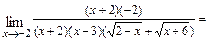
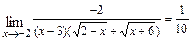Примечание. Данный предел легко вычислить и по правилу Лопиталя:

.

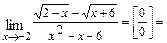
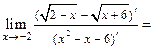
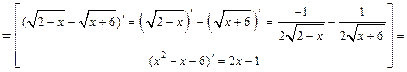
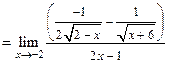
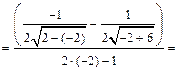
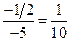в) 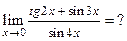При подстановке вместо переменной 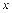её предельного значения 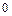получим неопределённость 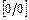. Вычислим предел по правилу Лопиталя. Получим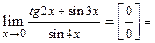

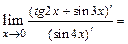
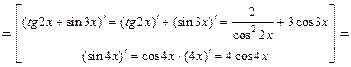
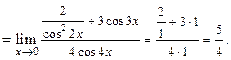
Ответ:

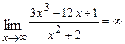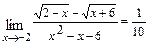а) ;б) ;в)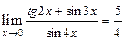

81-90. Для указанной функции требуется:

а) найти наибольшее и наименьшее значения функции 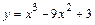на отрезке ;

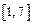б) составить уравнение касательной к графику функции 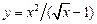в точке ;

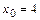в) провести полное исследование функции 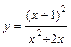, построить её график.

Решение а).

Наибольшее и наименьшее значения функции 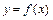непрерывной и кусочно-дифференцируемой (дифференцируемой, за исключением, быть может, конечного числа точек) на отрезке 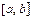достигается или в точках 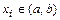, в которых 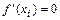или 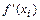не существует, или на концах отрезка.

1а)Находим первую производную функции:

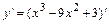
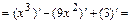
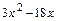
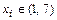и определяем внутренние критические точки функции , т.е. точки в которых 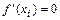или 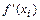не существует:

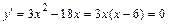
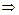
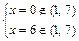, точек 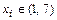в которых 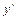не существует нет. Таким образом, единственной внутренней критической (стационарной) точкой функции на отрезке 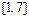является точка .

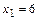2а)Вычисляем значения функции во внутренних критических точках и на концах отрезка : , , .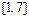

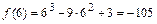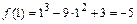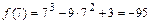3а)Сравниваем значения 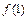, , 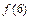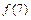и находим наименьшее и наибольшее значения функции на отрезке :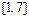

, .

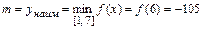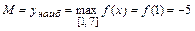Ответ: , .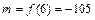

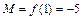Решение б).

Уравнение касательной к графику функции 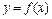в точке 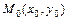имеет вид: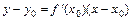

1б)Вычисляем значение функции в точке : .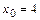

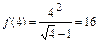2б) Находим первую производную функции: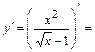

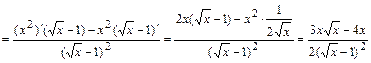и вычисляем её значение в точке : .

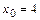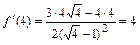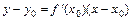
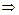
3б)Составляем уравнение касательной: 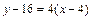изаписываем его в виде : .

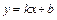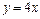Ответ: 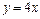- уравнение касательной.

Решение в).

Для построения графика непериодической функции нужно:

1) найти область определения функции;

2) найти область непрерывности функции и точки разрыва;

3) исследовать функцию на чётность, нечётность;

4) найти точки пересечения графика с осями координат;

5) найти асимптоты графика функции;

6) найти интервалы возрастания и убывания, экстремумы функции;

7) найти интервалы выпуклости, вогнутости и точки перегиба.

1в)Находим область определения функции: = ).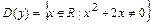

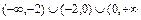2в)Поскольку данная функция является элементарной, то областью её непрерывности является область определения 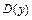, а точками разрыва являются точк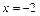и и 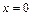, не принадлежащие множеству 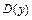, но являющиеся предельными точками этого множества (точками в любой окрестности которых содержатся точки данного множества). Исследуем характер разрыва в точках 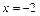и 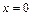, вычислив в них односторонние пределы функции:

, ,

, .

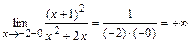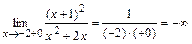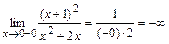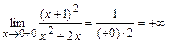Так как односторонние пределы функции в точках 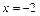и 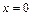- бесконечные, то данные точки являются точками бесконечного разрыва.

3в)Проверяем является ли функция чётной или нечётной. Так как область определения функции 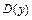= 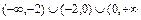) не симметрична относительно точки 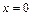, то данная функция – общего вида.

4в)Находим точки пересечения графика с осями координат.

Так как 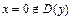, то точек пересечения графика с осью 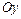нет.

Положим 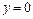и решим уравнение 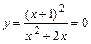. Его решением является 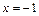. Следовательно, точка 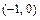- точка пересечения графика с осью .

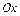5в)Находим вертикальные и наклонные асимптоты графика функции.

Прямая 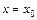является вертикальной асимптотой, тогда и только тогда, когда 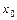является точкой бесконечного разрыва функции .

Так как точк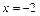и и 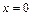- точки бесконечного разрыва данной функции, то вертикальными асимптотами графика функции являются прямые 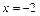и .

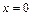Прямая 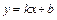является наклонной асимптотой графика функции при 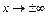тогда и только тогда, когда одновременно существуют конечные пределы: 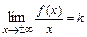и .

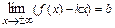Вычисляем сначала пределы при :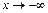

, .

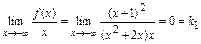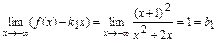В дальнейшем будем иметь в виду следующий часто встречающийся предел: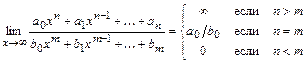

Следовательно 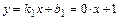, т.е. 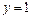- наклонная (горизонтальная) асимптота графика функции при .

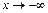Аналогично вычисляем пределы при 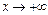: 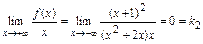, 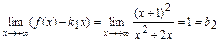Следовательно 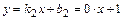, т.е. 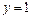- наклонная (горизонтальная) асимптота графика функции при .

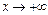6в)Определяем интервалы возрастания, убывания, экстремумы функции. Для этого находим первую производную функции:

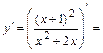
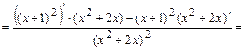
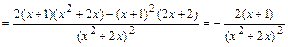
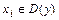и определяем критические точки функции , т.е. точки в которых 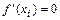или 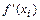не существует:

;

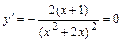
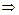
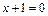
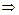
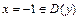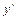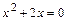
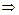
не существует пр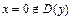и и .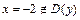

Таким образом, единственной критической (стационарной) точкой функции является точка .

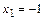Исследуем знак производной 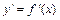в интервалах, на которые критические точки функции разбивают её область определения 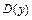, и найдём интервалы возрастания, убывания, экстремумы функции. Результаты исследования представим следующей таблицей:

	+	+
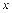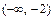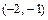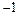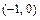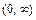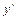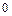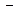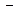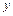	возрастает	возрастает		убывает	убывает

Так как при переходе слева направо через точку 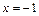производная 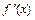меняет знак с «+» на « 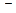», то точка 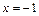является точкой локального максимума и .

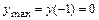7в)Определяем интервалы выпуклости, вогнутости, точки перегиба графика функции. Для этого находим вторую производную функции:

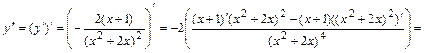
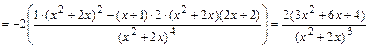
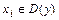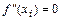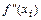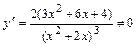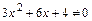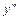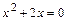
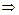
и определяем точки возможного перегиба , т.е. точки в которых или не существует: , так как (квадратное уравнение не имеет действительных корней); не существует пр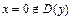и и .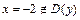

Таким образом, функция не имеет точек возможного перегиба.

Исследуем знак второй производной 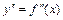в интервалах, на которые точки возможного перегиба функции разбивают её область определения 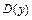, и найдём интервалы выпуклости, вогнутости, точки перегиба графика функции. Результаты исследования представим таблицей:

	+		+
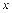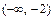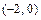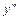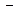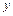	график вогнутый	график выпуклый	график вогнутый

Точек перегиба нет.

8в)На основании полученных результатов строим график функции:

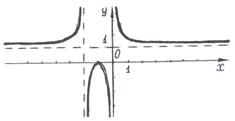
91 – 100.Для указанной функции 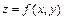требуется:

а)найти дифференциал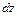и 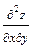, если ;

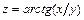б) найти локальные экстремумы, если .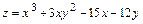

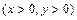Решение а).

Первый дифференциал функции 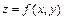имеет вид .

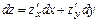Частные производные функции 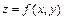вычисляются по обычным правилам дифференцирования функции одной переменной, в предположении, что если производная берётся по аргументу 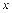(аргументу 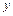), то другой аргумент 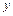(аргумент 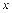) считается постоянным.

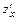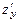1а) Находим частные производные первого порядка и функции

:

;

.

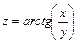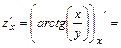
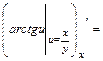
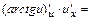
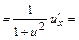
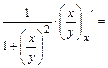
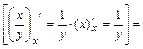
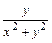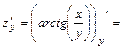
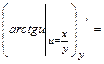
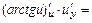
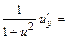
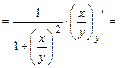
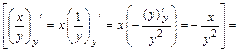
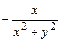Тогда первый дифференциал 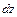функции имеет вид:

.

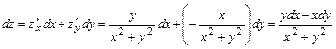2а) Вторую частную производную 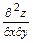(или кратко 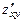) находим как первую частную производную по аргументу 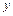от функции :

.

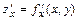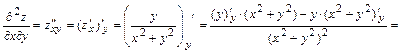
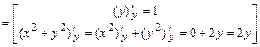
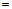
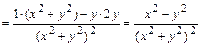Ответ: , .

Решение б).

Для нахождения локальных экстремумов дифференцируемой функции 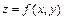необходимо:

1) Найти область определения 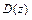функции.

2) Найти первые частные производные 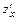и 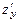функции.

3) Решить систему уравнений (необходимое условие экстремума) 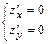и найти точки 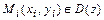(с учётом возможных дополнительных ограничений на значения аргументов 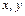) возможного локального экстремума функции.

4) Найти вторые частные производные 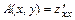, , 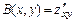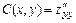; составить выражение 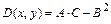и вычислить значения 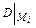и 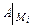в каждой точке 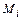возможного экстремума.

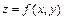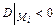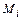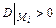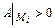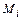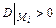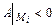5) Сделать вывод о наличии экстремумов функции , используя достаточное условие экстремума: если , то в точке экстремума нет; если и , то в точке - локальный минимум; если и , то в точке 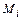- локальный максимум; если 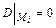, то требуется дополнительное исследование точки 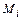(например, по определению).

6) Найти локальные экстремумы (экстремальные значения) функции.

1б)Находим область определения функции .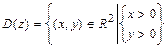

2б)Находим первые частные производные 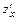и :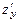

;

.

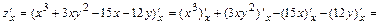
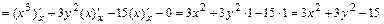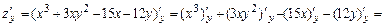
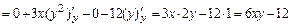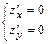
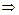
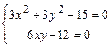
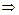
3б)Составим систему уравнений 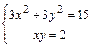и решим её. Получим четыре решения: 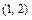, , 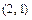, 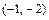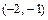. Из них точками возможного экстремума функции 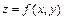в области 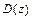являются только две точк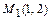и: и .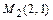

4б)Находим вторые частные производные:

;

;

,

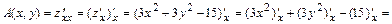
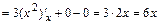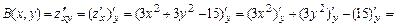
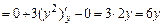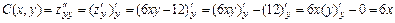составляем выражение 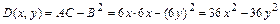и вычисляем:

; , .

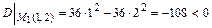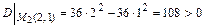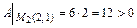5б)Делаем вывод о наличии экстремумов. Так как:

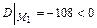, то в точке 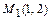экстремума нет;

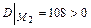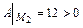, , то в точке 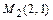- локальный минимум.

6б)Находим локальный минимум

.

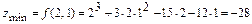Ответ: .

Раздел III. Интегральное исчисление.

101-110.Найти неопределённые интегралы:a)непосредственным интегрированием; б) заменой переменной интегрирования; в) интегрированием по частям.

а) ;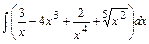

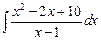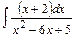б1) ; б2) ; б3) ;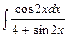

в) ;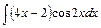

Нахождение неопределённого интеграла 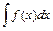состоит в таком преобразовании подынтегрального выражения 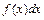, чтобы получить интегралы (возможно по новой переменной интегрирования) из таблицы основных интегралов (приложение 6.3).

Решение.

а) Интеграл вычислим непосредственным интегрированием. Получим: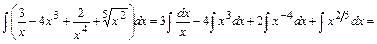

.

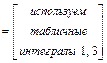
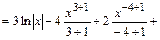
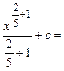
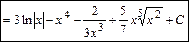б1)Интеграл вычислим методом замены переменной интегрирования.

Интеграл вида 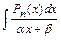, где 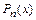- многочлен порядка 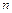, находят методом замены переменной с помощью подстановки .

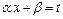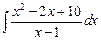
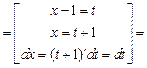
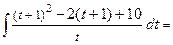
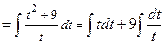
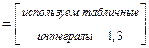
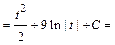
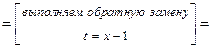
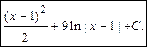
б2) Интеграл относится к интегралам вида 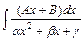. Для его вычисления сначала выделим полный квадрат в знаменателе подынтегральной функции, затем сделаем замену переменной интегрирования. Получим: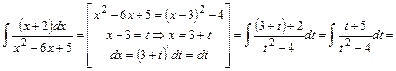

=[представляем интеграл в виде суммы интегралов] .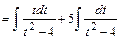

Вычислим каждый из интегралов в отдельности:

1)

.

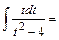
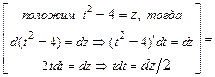
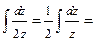
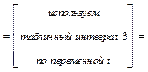
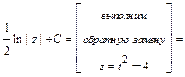
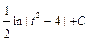2)

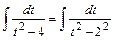
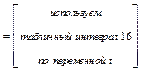
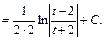
Тогда: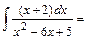

.

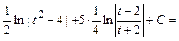
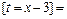
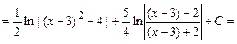
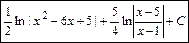Конечное выражение для неопределённого интеграла записывают, указывая одну из первообразных и добавляя к ней произвольную постоянную .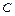

б3) Интеграл вычислим методом замены переменной интегрирования. Получим: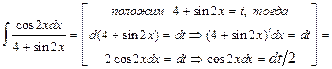

.

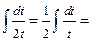
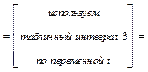
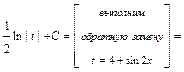
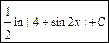в) Интеграл вычислим методом интегрирования по частям, используя формулу .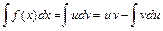

Положим: 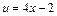, 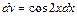. Найдём ,

.

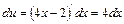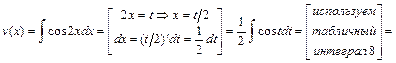
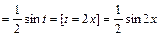Интеграл 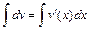в формуле интегрирования по частям вычисляется с точностью до постоянной, т.е. в качестве функции 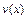выбирается одна из первообразных для функции .

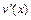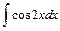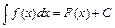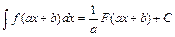Для вычисления интеграла можно использовать и следующее свойство неопределённого интеграла: если , то , где 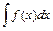- табличный интеграл. В данном случае, так как 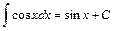, то .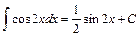

Тогда, получим:

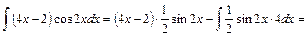
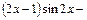
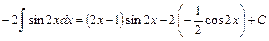
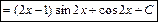
Определённый интеграл для функции 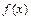, непрерывной на отрезке 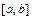, вычисляют по формуле Ньютона-Лейбница: 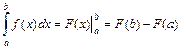, где 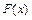-одна из её первообразных, используя для нахождения 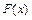все приёмы и методы вычисления неопределённых интегралов.

Следствиями формулы Ньютона-Лейбница являются:

1) формула интегрирования по частям 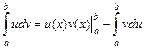, где функци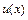и и 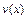непрерывно дифференцируемы на ;

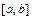2) формула замены переменной интегрирования

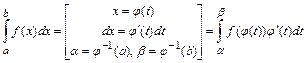, где функция 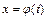- непрерывно дифференцируема на отрезке .

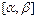Часто замена переменной в определённом интеграле выполняется с помощью подстановки 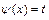по формуле: 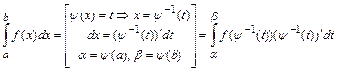, где функция 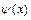- непрерывно дифференцируема на отрезке .

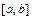111-120.Требуется вычислить:а) определённый интеграл ;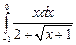

б) несобственный интеграл 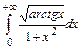(или установить его расходимость).

Решение.

а) Определённый интеграл вычислим заменой переменной интегрирования.

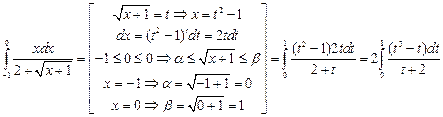
Последний интеграл вычисляем также заменой переменной.

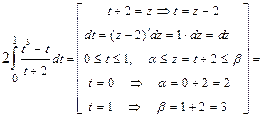
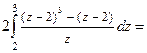
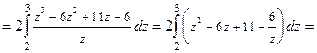
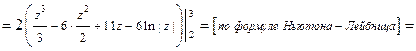
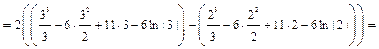
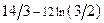. Ответ: .

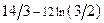б) По определению несобственного интеграла имеем 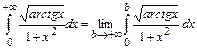. Определенный интеграл, стоящий под знаком предела, вычислим методом замены переменной: 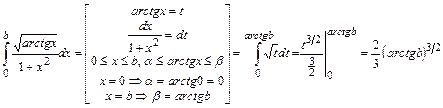Тогда .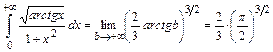

Ответ: Несобственный интеграл сходится и равен .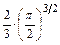

121-130.Вычислитьплощадь фигуры, ограниченной графиками указанных функций: