Дифференциальный усилитель

ЛЕКЦИЯ 9

расчёт эмиттерного повторителя

План лекции:

9.1. Расчёт рабочей точки эмиттерного повторителя

9.2. Эмиттерный повторитель как четырёхполюсник

Дифференциальный усилитель

9.1. Расчёт рабочей точки эмиттерного повторителя

Схема эмиттерного повторителя (ЭП) приведена на рис. 9.1.

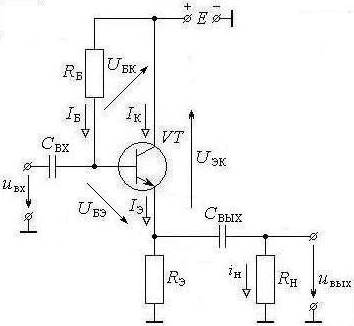
Рис. 9.1. Эмиттерный повторитель – схема принципиальная электрическая

Для схемы эмиттерного повторителя (каскад с ОК) входными величинами являются ток базы 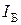и напряжение база-кол­лектор 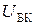, выходными − ток эмиттера 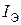и напряжение эмиттер-коллектор 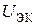(рис. 9.2).

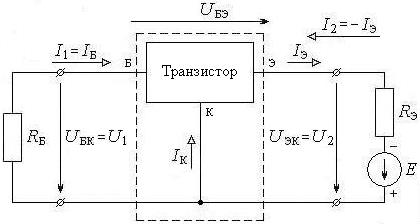
Рис. 9.2. Эмиттерный повторитель как четырёхполюсник (схема по постоянному току)

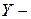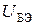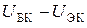Поэтому система уравнений ЭП в параметрах по постоянному току может быть записана через уравнения (7.1 с) и (7.1 а) с заменой в них напряжения на согласно схеме рис. 9.2:

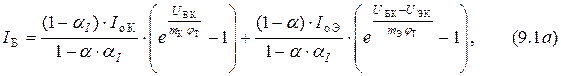
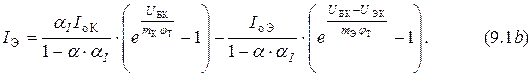
Так как уравнения трансцендентные, то выразить 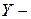параметры схемы по постоянному току в виде отдельных формул не представляется возможным.

Дать методику выбора рабочей точки ЭП!

9.2. Эмиттерный повторитель как четырёхполюсник

Рассмотрим расчёт параметров эмиттерного повторителя по переменному току на низких и средних частотах, когда на входе ЭП действует гармоническое напряжение малой амплитуды. В этом случае сопротивлениями разделительных конденсаторов схемы по сравнению с сопротивлениями резисторов можно пренебречь, а влияние паразитных ёмкостей транзистора на работу каскада можно не учитывать. Поэтому величина нагрузки по переменному току будет равна

Кроме того, нужно будет учесть внутреннее сопротивление 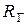источника гармонического сигнала 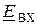(рис. 9.3).

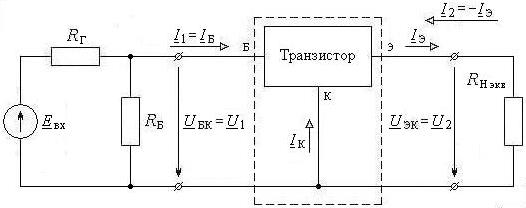
Рис. 9.3. Эмиттерный повторитель как четырёхполюсник (схема по переменному току)

Для малых приращений токов 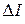и напряжений 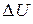система статических 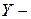параметров (9.1) преобразуется в систему дифференциальных 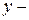параметров:

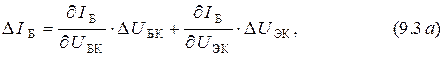
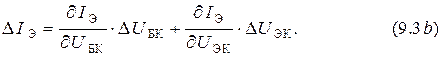
Заменив приращения на комплексные амплитуды, получим в общем виде систему уравнений четырёхполюсника для дифференциальных 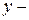параметров транзистора в схеме с ОК:

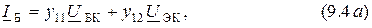
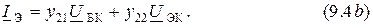
Дифференцируя уравнения (9.1) согласно выражениям (9.3), получаем формулы 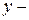параметров

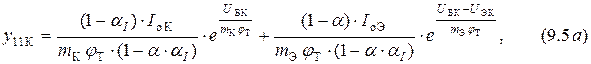
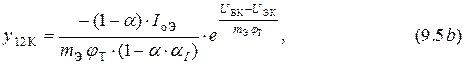
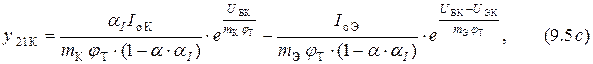
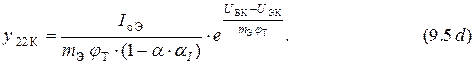
Выходное сопротивление ЭП можно рассчитать по формуле

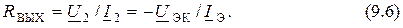
Заменим в выражении тока 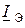(знаменатель формулы (9.6)) входное напряжение 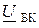в формуле (9.4 b), используя формулу (9.4 a). С этой целью найдём связь тока 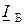с напряжением 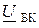через известное внутреннее сопротивление источника входной эдс. Оно представляет собой параллельное соединение 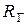и :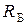

По закону Ома

Подставляя эту формулу в выражение (9.4 a) и преобразуя полученное уравнение, находим соотношение

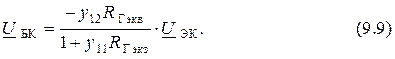
Заменим напряжение 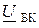в формуле (9.4 b) соотношением (9.9) и после преобразования получим

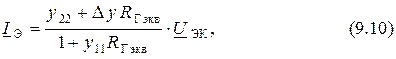
где

Поэтому находим величину выходного сопротивления ЭП

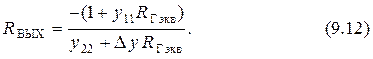
Коэффициент передачи ЭП находим по формуле

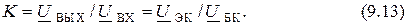
Выразим выходной ток через сопротивление нагрузки

Подставляя это выражение в формулу (9.4 b), получим

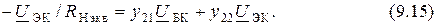
Отсюда находим

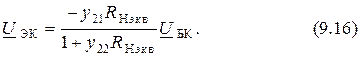
Поэтому получаем выражение

Найдём формулу входного сопротивления без учёта влияния :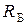

Подставим выражение (9.16) в формулу (9.4 a)

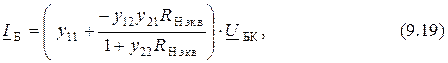
а полученный результат – в формулу (9.18). После преобразования находим выражение

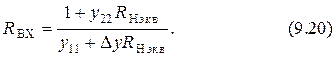
Входное сопротивление ЭП с учётом 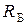равно

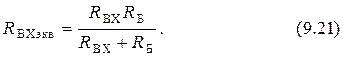
Коэффициент передачи ЭП от источника входной эдс равен

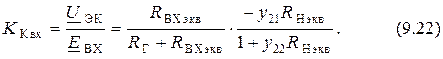
Дать количественные величины!