Работа 4. исследование процесса истечения воздуха
ЧЕРЕЗ СУЖИВАЮЩЕЕСЯ СОПЛО
Цели работы
Исследование зависимости массового расхода воздуха через суживающееся сопло от отношения давления за соплом к давлению перед соплом. Определение коэффициентов потери скорости и энергии для реального сопла.
Основные положения
Канал, в котором с уменьшением давления скорость газового потока возрастает, называется соплом;канал, в котором скорость газа уменьшается, а давление возрастает, называется диффузором.
Поскольку назначением сопла является преобразование потенциальной энергии рабочего тела в кинетическую, для анализа происходящего в нем процесса начальная скорость потока является несущественной, и можно принять W1 = 0.
Тогда уравнение первого закона термодинамики при адиабатном истечении рабочего тела через сопло принимает вид
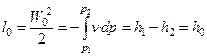 .
.
Исходя из равенства W02/2 = h0, теоретическую скорость истечения рабочего тела через сопло в рассматриваемом случае можно определить по формуле
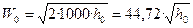 , м/с,
, м/с,
Здесь h0 выражено в кДж/кг. Это соотношение справедливо для любого рабочего тела.
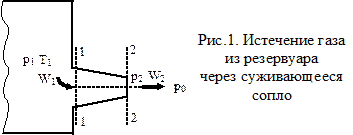 Рассмотрим адиабатное истечение газа через суживающееся сопло из резервуара (рис.1) достаточно большого объема, в котором изменением давления можно пренебречь (P ≈ Const).
Рассмотрим адиабатное истечение газа через суживающееся сопло из резервуара (рис.1) достаточно большого объема, в котором изменением давления можно пренебречь (P ≈ Const).
В резервуаре газ имеет параметры Р1, T1, v1 (ρ1), а на выходе из сопла – Р2, Т2, v2 (ρ2), W2; давление среды, в которую происходит истечение газа, обозначим Р0. Основной характеристикой процесса истечения является отношение конечного давления к начальному, т. е. величина β = Р0/Р1.
В зависимости от отношения давлений можно выделить три характерных режима истечения газа: при β > βкр – докритический, β = βкр – критический и β < βкр– сверхкритический режимы.
Значение β, при котором расход газа достигает максимума, называется критическим βкр, и находится по формуле
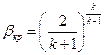 . (1)
. (1)
Как и показатель адиабаты, величина βкр является физической константой газа, т. е. одной из характеристик его физических свойств.
Скорость газа на выходе из суживающегося сопла определяется по формуле:
для первого случая, когда β > βкр Р2 = Р0,
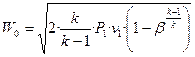 ;
;
для второго и третьего случая, когда β = βкр Р2 = Ркр = Р1·βкр = Р0 и β < βкр Р2 = Ркр = Ρ1·βкр > Ρ0
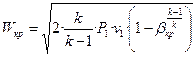 ,
,
или, подставив значение βкр из формулы (1), получим:
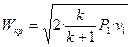 ,
,
тогда при условиях адиабатного истечения
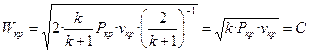 .
.
Полученная формула показывает, что критическая скорость истечения газа из сопла равна скорости распространения звуковой волны в этом газе при его параметрах Ркр и vкр, т е местной скорости звука С в выходном сечении сопла.
В этом содержится физическое объяснение тому, что при снижении внешнего давления Р0 ниже Ркр скорость истечения не изменяется, а остается равной Wкр.
В отличие от теоретического - изоэнтропийного действительный процесс истечения реального газа происходит при трении частиц газа между собой и о стенки канала. При этом работа, затрачиваемая на преодоление сил трения, преобразуется в теплоту, в результате чего температура и энтальпия газа в выходном сечении канала возрастают.
Истечение газа с трением становится необратимым процессом и сопровождается увеличением энтропии.
На рис. 2 в sh–координатах представлены процессы расширения газа 1–2 при истечении без трения и 1–2д при истечении с трением. При одинаковом перепаде давлений Р1 – Р2 действительный теплоперепад Δhд = h1–h2д меньше располагаемого Δh = h1 – h2.
В результате этого действительная скорость истечения газа оказывается меньше теоретической.
Отношение разности располагаемого и действительного теплоперепадов (потери теплоперепада) к располагаемому теплоперепаду называется коэффициентом потери энергии
 ζс = (Δh – Δhд)/Δh. (2)
ζс = (Δh – Δhд)/Δh. (2)
Отсюда
Δhд = (1 – ζс)·Δh.
Коэффициентом потери скорости называется отношение действительной скорости истечения к теоретической
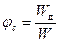 . (3)
. (3)
Коэффициент потери скорости, учитывающий уменьшение действительной скорости по сравнению с теоретической, в современных соплах равен 0,95 – 0,98 .
Отношение действительного теплоперепада Δhд к теоретическому Δh или действительной кинетической энергии Wд2/2 к теоретической W2/2 называется коэффициентом полезного действия канала:
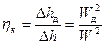 . (4)
. (4)
С учетом выражений (2) и (3)
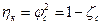 . (5)
. (5)
