Канонический вид квадратичной формы

Квадратичная форма называется канонической, если вс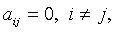е т. е.

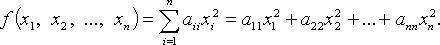
Всякую квадратичную форму можно привести к каноническому виду с помощью линейных преобразований. На практике обычно применяют следующие способы.

1. Ортогональное преобразование пространства :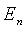

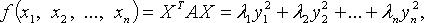
где 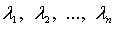- собственные значения матрицы A.

2. Метод Лагранжа - последовательное выделение полных квадратов. Например, если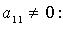

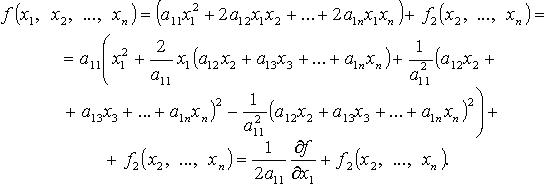
Затем подобную процедуру проделывают с квадратичной формой 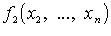и т. д. Если в квадратичной форме все 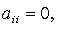но есть 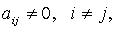то после предварительного преобразования дело сводится к рассмотренной процедуре. Так, если, например, 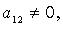то полагаем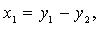

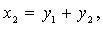
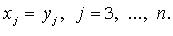
3. Метод Якоби (в случае, когда все главные миноры 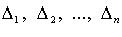квадратичной формы отличны от нуля):

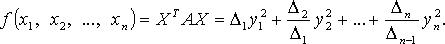
№31

Любая прямая на плоскости может быть задана уравнением первого порядка

Ах + Ву + С = 0,

причем постоянные А, В не равны нулю одновременно. Это уравнение первого порядка называют общим уравнением прямой.В зависимости от значений постоянных А,В и С возможны следующие частные случаи:

• C = 0, А ≠0, В ≠ 0 – прямая проходит через начало координат

• А = 0, В ≠0, С ≠0 { By + C = 0}- прямая параллельна оси Ох

• В = 0, А ≠0, С ≠ 0 { Ax + C = 0} – прямая параллельна оси Оу

• В = С = 0, А ≠0 – прямая совпадает с осью Оу

• А = С = 0, В ≠0 – прямая совпадает с осью Ох

Уравнение прямой может быть представлено в различном виде в зависимости от каких – либо заданных начальных условий.

Прямая в пространстве может быть задана:

1) как линия пересечения двух плоскостей,т.е. системой уравнений:

A₁ x + B₁ y + C₁ z + D₁ = 0, A₂ x + B₂ y + C₂ z + D₂ = 0; (3.2)

2) двумя своими точками M₁(x₁, y₁, z₁) и M₂(x₂, y₂, z₂), тогда прямая, через них проходящая, задается уравнениями:

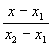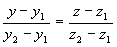= ; (3.3)

3) точкой M₁(x₁, y₁, z₁), ей принадлежащей, и вектором a(m, n, р), ей коллинеарным. Тогда прямая определяется уравнениями:

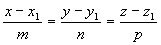. (3.4)

Уравнения (3.4) называются каноническими уравнениями прямой.

Векторa называется направляющим вектором прямой.

Параметрические уравнения прямой получим, приравняв каждое из отношений (3.4) параметру t:

x = x₁ +mt, y = y₁ + nt, z = z₁ + рt. (3.5)

Решая систему (3.2) как систему линейных уравнений относительно неизвестных x и y, приходим к уравнениям прямой впроекциях или к приведенным уравнениям прямой:

x = mz + a, y = nz + b. (3.6)

От уравнений (3.6) можно перейти к каноническим уравнениям, находя z из каждого уравнения и приравнивая полученные значения:

.

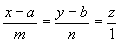От общих уравнений (3.2) можно переходить к каноническим и другим способом, если найти какую-либо точку этой прямой и ее направляющий вектор n= [n₁, n₂], где n₁(A₁, B₁, C₁) и n₂(A₂, B₂, C₂) - нормальные векторы заданных плоскостей. Если один из знаменателей m, n или р в уравнениях (3.4) окажется равным нулю, то числитель соответствующей дроби надо положить равным нулю, т.е. система

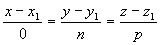
равносильна системе 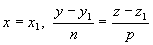; такая прямая перпендикулярна к оси Ох.

Система 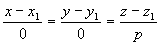равносильна системе x = x₁, y = y₁; прямая параллельна оси Oz.

№32

Всякое уравнение первой степени относительно координат x, y, z

Ax + By + Cz +D = 0 (3.1)

задает плоскость, и наоборот: всякая плоскость может быть представлена уравнением (3.1), которое называетсяуравнением плоскости.

Вектор n (A, B, C ), ортогональный плоскости, называется нормальным вектором плоскости. В уравнении (3.1) коэффициенты A, B, C одновременно не равны 0.

Особые случаи уравнения (3.1):

1. D = 0, Ax+By+Cz = 0 - плоскость проходит через начало координат.

2. C = 0, Ax+By+D = 0 - плоскость параллельна оси Oz.

3. C = D = 0, Ax +By = 0 - плоскость проходит через ось Oz.

4. B = C = 0, Ax + D = 0 - плоскость параллельна плоскости Oyz.

Уравнения координатных плоскостей: x = 0, y = 0, z = 0.

№33-36

Прямая может принадлежать и не принадлежать плоскости. Она принадлежит плоскости, если хотя бы две точки ее лежат на плоскости.

Если прямая не принадлежит плоскости, она может быть параллельной ей или пересекать ее.

Прямая параллельна плоскости, если она параллельна другой прямой, лежащей в этой плоскости.

Прямая может пересекать плоскость под различными углами и, в частности, быть перпендикулярной ей.

Точка по отношению к плоскости может быть расположена следующим образом: принадлежать или не принадлежать ей. Точка принадлежит плоскости, если она расположена на прямой, расположенной в этой плоскости.

В пространстве две прямые могут либо пересекаться, либо быть параллельными, либо быть скрещенными.

Параллельность отрезков прямых сохраняется в проекциях.

Если прямые пересекаются, то точки пересечения их одноимённых проекций находятся на одной линии связи.

Скрещивающиеся прямые не принадлежат одной плоскости, т.е. не пересекаются и не параллельны.

на чертеже одноименные проекции прямых, взятые отдельно, имеют признаки пересекающихся или параллельных прямых.

№37

Эллипс. Эллипсом называется геометрическое место точек, для которых сумма расстояний до двух фиксированных точек (фокусов) есть для всех точек эллипса одна и та же постоянная величина (эта постоянная величина должна быть больше, чем расстояние между фокусами).

Простейшее уравнение эллипса

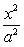
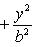
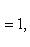
где a - большая полуось эллипса, b - малая полуось эллипса. Если 2c - расстояние между фокусами, то между a, b и c (если a > b) существует соотношение

a² - b² = c².

Эксцентриситетом эллипса называется отношение расстояния между фокусами этого эллипса к длине его большой оси

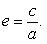
У эллипса эксцентриситет e < 1 (так как c < a), а его фокусы лежат на большой оси.

№38

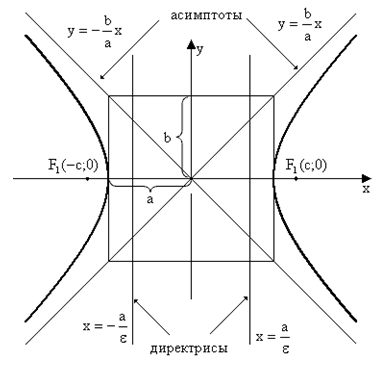
Уравнение гиперболы, изображенной на рисунке .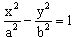

Параметры:
a, b – полуоси;
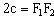- расстояние между фокусами,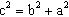
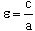- эксцентриситет;
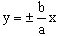- асимптоты;
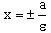- директрисы.
Прямоугольник, изображенный в центре рисунка – основной прямоугольник, его диагонали есть асимптоты.

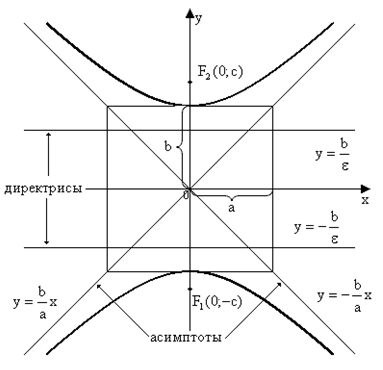
Уравнение гиперболы, изображенной на рисунке .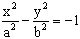

Параметры:
a, b – полуоси;
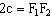- расстояние между фокусами,
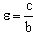- эксцентриситет;
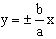- асимптоты;
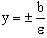- директрисы.
Прямоугольник, изображенный в центре рисунка – основной прямоугольник, его диагонали есть асимптоты.

№39

Парабола. Параболой называется геометрическое место точек, каждая из которых одинаково удалена от заданной фиксированной точки и от заданной фиксированной прямой. Точка, о которой идет речь в определении, называется фокусом параболы, а прямая - ее директрисой.

Простейшее уравнение параболы

y² = 2px. (*)

Входящая в это уравнение величина p называется параметром параболы. Параметр параболы равен расстоянию от директрисы параболы до ее фокуса.

Координаты фокуса F параболы (*) 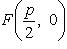. (фокус параболы лежит на ее оси симметрии) Уравнение директрисы параболы (*)

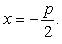
Эксцентриситет параболы e = 1.

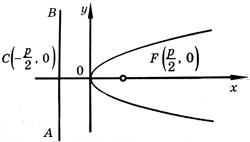
y² = 2px (p > 0)

№40