Требования безопасности в аварийных ситуациях.

5.1. При обнаружении неисправности в работе электрических устройств, находящихся под напряжением, повышенном их нагревании, появлении искрения, запаха горелой изоляции, задымлении и т.д. немедленно отключить источник электропитания и сообщить об этом преподавателю.

5.2. В случае, если разбилась лабораторная посуда или приборы из стекла, не собирать их осколки незащищенными руками, а использовать для этой цели щетку и совок.

5.3. При разливе легковоспламеняющейся жидкости и ее загорании немедленно сообщить об этом преподавателю и по его указанию покинуть помещение.

5.4. При получении травмы сообщить об этом преподавателю, который немедленно должен оказать первую помощь пострадавшему и сообщить администрации кафедры, при необходимости помочь в отправке пострадавшего в ближайшее лечебное учреждение.

5.5. Оказание первой доврачебной помощи пострадавшему при ожогах огнём, паром, горячей водой: осторожно снять одежду, перевязать обожжённое место стерилизованным материалом. При ожогах кислотами, щёлочью, реактивами: промыть обожжённое место сильной струёй воды и наложить примочку из содового раствора.

5.6. Оказание первой доврачебной помощи пострадавшему при слабом кровотечении: закрыть рану стерильным материалом и плотно забинтовать. При артериальном кровотечении: наложить жгут или «закрутку» выше места раны поверх ткани одежды на время не более 1,5 (летом) или 2 часа (зимой).

5.7. Оказание первой доврачебной помощи при поражении электрическим током:

¾ освободить пострадавшего от действия тока, отключив напряжение или оттащив его от проводов при помощи диэлектрических перчаток;

¾ при необходимости сделать ему пострадавшему искусственное дыхание и закрытый массаж сердца (после вдувания воздуха в лёгкие пострадавшему, 5-6 раз надавить на нижнюю треть грудной клетки; за 1 мин. производить 48-50 сжатий грудной клетки и 10-12 вдуваний воздуха в лёгкие).

5.8 Об аварийной ситуации сообщить руководству кафедры для проведения расследования.

ЛАБОРАТОРНАЯ РАБОТА № 3.1
ИЗУЧЕНИЕ ХАРАКТЕРИСТИК ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ

Цель: изобразить графически сечение эквипотенциальных поверхностей электростатического поля, созданного заданной конфигурацией электрических зарядов; используя изображение эквипотенциальных поверхностей, построить силовые линии электростатического поля заданной конфигурации зарядов; при помощи полученной картины силовых и эквипотенциальных линий проверить справедливость формулы связи напряжённости электрического поля с его потенциалом.

Материалы и оборудование: источник постоянного тока, ванна из диэлектрика, набор электродов различной формы, вольтметр, реостат, нуль-гальванометр.

Практическое значение: рассмотренный круг вопросов лежит в основе расчетов картин электростатических полей, позволяет смоделировать реальное распределение электростатических полей произвольной системы заряженных тел, что важно, с точки зрения техники безопасности и при конструировании конденсаторов, электронных линз и других электронных приборов.

1 ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ

Электрические поля, которые не меняются со временем и создаются неподвижными заряженными частицами, называют электростатическими.

Основными характеристиками электростатического поля в данной точке есть векторная величина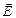- напряженность и скалярная величина - потенциал φ.

Напряженность - силовая характеристика поля, векторная величина, численно равная силе, действующей на единичный положительный точечный заряд, помещенный в данную точку поля:

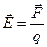(1.1)

Из определения следует, что сила, действующая со стороны электрического поля на точечный заряд, равна:

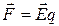(1.2)

Единица измерения напряженности электрического поля [В/м].

Потенциал - энергетическая характеристика электрического поля, скалярная величина, численно равная потенциальной энергии единичного точечного положительного заряда, помещенного в данную точку поля:

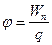(1.3)

Потенциал измеряется в вольтах: [1В= 1Дж/1Кл]. Потенциал определяется с точностью до произвольной постоянной (как и потенциальная энергия) и может принимать положительные и отрицательные значения. Физический же смысл имеет величина - разность потенциалов. Разность потенциалов связана с работой сил электрического поля по перемещению точечного заряда следующим образом:

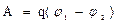(1.4)

где j₁ и j₂- потенциалы начальной и конечной точек положения заряда q.

Электрическое поле наглядно изображается с помощью силовых линий. Силовой линией электрического поля называется линия, в каждой точке которой касательная совпадает с вектором напряженности поля.

Вектор напряженности поля положительного заряда направлен вдоль радиуса от заряда, отрицательного заряда – вдоль радиуса по направлению к заряду. Исходя из положительного заряда (или входя в отрицательный заряд) силовые линии теоретически простираются до бесконечности (рис. 1.1 – а, б).

Силовые линии одноименных зарядов не пересекаются, в этом заключается природа отталкивания одноименных зарядов (рис. 1.1 – в).

Силовые линии двух разноименных зарядов замкнутые, они начинаются на положительном и заканчиваются на отрицательном заряде (рис. 1.1 – г).

В электрическом поле можно построить поверхности, которые являются геометрическим местом точек с одинаковым потенциалом - эквипотенциальные поверхности. Эквипотенциальные поверхности и линии напряженности является ортогональным между собой. Напряженность поля связана с потенциалом соотношением

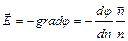, (1.5)

где производная берётся по нормали к эквипотенциальной поверхности, то есть в направлении быстрого изменения потенциала. Как правило, электрическое поле графически изображают так, чтобы при переходе от одной эквипотенциальной поверхности к другой прирост потенциала был тот же. При этом в местах, где поверхности близко подходят друг к другу, напряженность поля максимальна.

Теорема Остроградского-Гаусса для электростатического поля: поток вектора напряженности электростатического поля Ф_Е в вакууме сквозь произвольную замкнутую поверхность dS равен алгебраической сумме зарядов, заключенной внутри этой поверхности, деленной на ε₀:

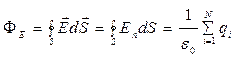. (1.6)

Теоремой Остроградского-Гаусса для электростатического поля утверждается, что поток пропорционален количеству источников поля, находящихся в объеме V.

Теорема Гаусса: поток вектора напряженности электрического поля Ф_Е через произвольную замкнутую поверхность dS пропорционален полному заряду, находящемуся в объеме, ограниченному этой поверхностью:

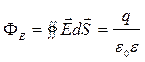. (1.7)

Эта математическая запись представляет собой теорему Гаусса в интегральной форме.

Согласно теореме Остроградского-Гаусса:

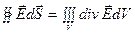. (1.8)

Выразим заряд через объемную плотность заряда ρ: 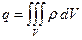и подставим в теорему Гаусса:

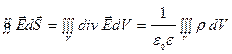. (1.9)

Отсюда следует, что дивергенция вектора напряженности электростатического поля прямо пропорциональна объемной плотности заряда:

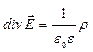. (1.10)

Это выражение представляет теорему Гаусса в дифференциальной форме.

Дивергенция характеризует плотность силовых линий поля. Из теоремы Гаусса следует, что, чем больше плотность силовых линий, тем больше напряженность, т.е. тем сильнее поле.

2 ОПИСАНИЕ ЭКСПЕРИМЕНТАЛЬНОЙ УСТАНОВКИ

На рис. 1.2 изображена схема установки для изучения электростатического поля в растворе электролита (применять воду).

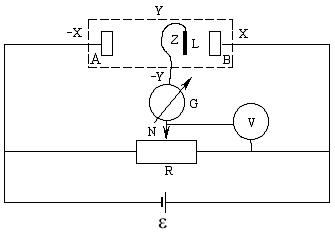
Рисунок 1.2 - Схема изучения электростатического поля

На дне ванны (штриховая линия на рис. 1.2), изготовленной из электроизоляционного материала, размещена миллиметровая бумага с нанесенной координатной сеткой, которую изолируют от попадания на нее электролита. Металлические электроды А и В погружают в электролит на концах координатного поля ванны. Напряжение подается на электроды от источника постоянного тока ε. В измерительную часть схема входят также вольтметр V, реостат R, нуль-гальванометр G.

Подвижным контактом N потенциометра можно установить различные значения потенциала относительно электродов. Перемещаем зонд Z в электрическом поле до тех пор, пока гальванометр покажет, что потенциалы в точках L и N одинаковы (гальванометр показывает ноль, ток в цепи зонда и гальванометра отсутствует). Координаты точки L находим по координатной сетке ванны. При неизменном положении подвижного контакта N перемещаем зонд Z вокруг электродов и ищем новые точки с таким же потенциалом. Записываем координаты этих точек.

Изменяя положение контакта N на потенциометре, получим семью эквипотенциальных поверхностей для данной пары электродов.

3 ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ

1. Составить электрическую цепь по схеме рис 1.2 с электродами.

2. Поставить зонд щуп на расстоянии 2 см от одного из электродов и переместить ползунок потенциометра в положение, когда через гальванометр ток не проходит. Перемещая зонд, определить ряд точек, отвечающих этому потенциалу (их должно быть не менее 8-10). Координаты точек и значения потенциала φ₁ занести в таблицу 1.1.

3. Повторить измерения, в пункте 2 при фиксированном значении потенциалов φ₂ и φ₃. Координаты точек и значение φ₂ и φ₃ занести в таблицу 1.1.

Таблица 1.1 – Экспериментальные данные

φ1	x
y
φ2	x
y
φ3	x
y

4. Записать в форму и координаты электродов для построения их на миллиметровой бумаге.

4 ОБРАБОТКА РЕЗУЛЬТАТОВ ЭКСПЕРИМЕНТА

1. Для каждого фиксированного значения потенциалов φ₁, φ₂, φ₃ наметить систему эквипотенциальных поверхностей на миллиметровой бумаге. У концов каждой линии, соответствующей определенной эквипотенциальной поверхности на графике, записать соответствующие значения потенциалов.

2. По полученным системам эквипотенциальных поверхностей построить для всех изученных полей картины силовых линий. Помните, что силовые линии начинаются и заканчиваются на заряженных телах и перпендикулярны эквипотенциальным линиям.

3. Для трех точек на двух эквипотенциальных поверхностях оцените величину напряженности электрического поля по формуле (1.5).

4. Оцените величину силы, действующей на электрон, помещенный в некоторую точку исследуемого поля.

5. Рассчитайте работу по перемещению электрона между двумя точками в исследуемом поле.

5 КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Дайте определение электростатического поля и его характеристик.

2. Как наглядно изображается электростатическое поле?

3. Могут ли пересекаться линии вектора напряженности электрического поля?

4. Изобразите графически поле одного положительного заряда, одного отрицательного заряда и системы зарядов.

5. Какая связь между напряженностью и потенциалом электростатического поля?

6. Что называется эквипотенциальной поверхностью? Могут ли пересекаться эквипотенциальные линии? Почему?

7. Какое ускорение приобретает электрон, двигаясь по эквипотенциальной линии?

8. Сформулируйте теорему Остроградского – Гаусса.

9. Выведите выражение теоремы Гаусса в дифференциальной форме.

10. . Какое поле называют потенциальным? Показать, что электростатическое поле потенциальное.

11. Показать, что силовые линии напряженности перпендикулярны эквипотенциальных поверхностей.

12. Воспользовавшись теоремой Гаусса найдите выражения для нахождения напряженности поля созданного:

а) бесконечного плоского однородно заряженного плоского слоя;

б) однородно заряженного шара;

в) однородно заряженной сферы;

г) однородно заряженной бесконечной цилиндрической поверхности.

13. Какую физическую величину называют объемной плотностью заряда? Чему она равна?

14. Как определяется работа электрического поля по перемещению заряда?

ЛИТЕРАТУРА [1, c.190-193], [2, c.9-23], [3, c.116-128], [4, c.13-48]

ЛАБОРАТОРНАЯ РАБОТА 3.2
ОПРЕДЕЛЕНИЕ РАБОЧИХ ХАРАКТЕРИСТИК Li – ИОННОГО АККУМУЛЯТОРА

Цель работы:определить внутреннее сопротивление и КПД Li – ионного аккумулятора.

Материалы и оборудование: Li – ионный аккумулятор, микросхема ZС10500, вольтметр, амперметр, магазин сопротивлений, ключи.

Практическое значение: аккумулятор на основе лития широко распространен в различных приложениях современной электроники, при помощи его выполняется электропитание большого количества мобильных и автономных устройств: телефонов, фото и видеокамер, ноутбуков, и др.

ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ

Аккумулятор – это химический источник тока. Принцип работы аккумулятора основан на преобразовании химической энергии в электрическую. Самыми энергоемкими аккумуляторами являются литиевые (материалом электрода является металлический литий).

На рисунке 2.1 представлен механизм заряда-разряда и устройство литий-ионного аккумулятора. В качестве анода в таких батареях наиболее часто применяют углеродные материалы, в качестве катода обычно используют слоистый оксид LiCoO₂.

Электролит представлен смесью типичных органических карбонатов содержащие комплексы лития. Для того чтобы отделить анод от катода используют очень тонкий лист микро-перфорированного пластика. Когда литий-ионная батарея заряжается, ионы лития перемещаются от катода к аноду, в то время как поток электронов течет по внешней электрической цепи.

Во время разряда происходит обратный процесс (рис. 2.1).

Электрический ток представляет собой упорядоченное (направленное) движение электрически заряженных частиц или заряженных макроскопических тел.

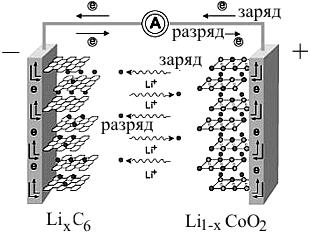
Рисунок 2.1 – Устройство литий – ионного аккумулятора

Физической характеристикой тока является сила тока. Сила тока характеризует заряд, протекающий через поперечное сечение проводника в единицу времени:

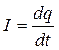. (2.1)

В СИ: ; .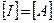

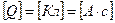Для однородного участка цепи (рис. 2.2) выполняется закон Ома. Он представляет вольтамперную характеристику цепи. Закон Ома (для участка цепи) в интегральной форме установлен экспериментально: сила тока прямо пропорциональна напряжению и обратно пропорциональна сопротивлению этого участка:

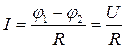(2.2)

где 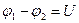- разность потенциалов или напряжение, [В];

R – электрическое сопротивление, [Ом].

Сопротивление R проводников представляет собой количественную меру противодействия проводника электрическому току. Сопротивление проводников зависит от материалов, формы, размеров, температуры и т.д. Сопротивление длинного проводника определяется по формуле:

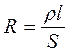, (2.3)

где l – длина проводника, S – площадь сечения, 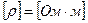– удельное сопротивление.

При последовательном соединении сопротивлений (рис. 2.3) заряд, проходящий через сечение проводников, остается постоянным. Следовательно, сила тока на каждом из участков тоже остается неизменной:

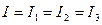; (2.4)

напряжение равно сумме падений напряжения на каждом из участков:

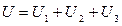; (2.5)

сопротивление равно сумме сопротивлений каждого из участков:

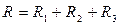. (2.6)

Если цепь состоит из n одинаковых сопротивлений, соединенных последовательно, то полное сопротивление определяется уравнением:

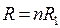. (2.7)

При параллельном соединении (рис. 2.4) согласно закону сохранения электрического заряда сила тока в цепи равна сумме силы тока на каждом из участков:

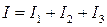; (2.8)

напряжение во всей цепи при параллельном соединении равно напряжению на каждом из участков:

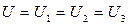. (2.9)

обратное значение сопротивления цепи равно сумме обратных значений сопротивлений каждого участка:

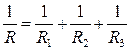. (2.10)

Если цепь состоит из n одинаковых сопротивлений, соединенных параллельно, то полное сопротивление определяется уравнением:

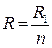. (2.11)

Для существования электрического тока в цепи необходимо наличие сторонних сил. Сторонними называются силы неэлектростатического происхождения, действующие на заряды со стороны источников тока и вызывающие перемещение электрических зарядов внутри источника постоянного тока. В аккумуляторах сторонние силы имеют химическую природу, в генераторах – электромагнитную. Сторонние силы совершают работу по разделению зарядов и поддержанию разности потенциалов на концах цепи.

Количественной характеристикой сторонних сил является электродвижущая сила (ЭДС). ЭДС – физическая величина, численно равная отношению работы сторонних си по перемещению заряда к величине этого заряда:

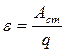. (2.12)

Основные внешние электрические характеристики аккумуляторной батареи – это внутреннее сопротивление r и КПД η источника тока.

При включении батареи в режим разрядки через резистор R в цепи течет ток I, который по закону Ома для полной цепи равен:

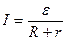(2.13)

Ток при коротком замыкании (R = 0) принимает максимальное значение

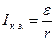(2.14)

Для двух различных значений R

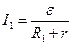
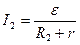(2.15)

Тогда

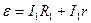
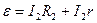(2.16)

Приравниваем

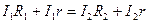
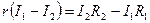
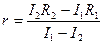(2.17)

Мощность, выделенная во всей цепи, получим

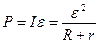. (2.18)

Аналогично преобразуем выражение для мощности, выделенной во внешней части цепи:

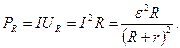(2.19)

Как видно из формул (2.18) и (2.19), мощность, выделенная во внешней цепи, и полная мощность источника тока зависят от ЭДС источника, его внутреннего сопротивления и сопротивления внешней цепи. Так как ЭДС источника и его внутреннее сопротивление, являющиеся характеристиками источника тока, не изменяются, то можно сказать, что как полная мощность, так и мощность, выделенная во внешней цепи, являются функциями сопротивления нагрузки R, т.е.

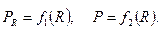
Так как при R=0 мощность P_R=0, а при 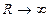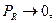то функция 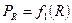должна иметь хотя бы один максимум. Найдем R, при котором P_R принимает максимальное значение. Дифференцируя (2.19) по R и приравнивая нулю, получим:

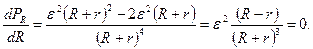
Так как ЭДС источника 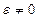, то R= r.

Итак, выделяемая во внешней цепи мощность максимальна, если внешнее сопротивление цепи равно внутреннему сопротивлению источника тока.

Любой источник тока можно охарактеризовать коэффициентом полезного действия (КПД)

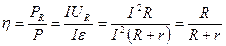(2.20)

Из формулы (2.20) видно, что КПД источника тока есть функция сопротивления внешней цепи: 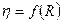.