Взаимное расположение прямых.

Угол между прямыми. Условия параллельности и перпендикулярности прямых.

Пол углом между этими прямыми понимают угол между направляющими векторами S₁ и S₂.

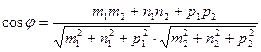
Для нахождения острого угла между прямыми L₁ и L₂ числитель правой части формулы следует взять по модулю.

Если прямые L₁ и L₂ перпендикулярны, то в этом и только в этом случае имеем cos 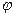=0. следовательно, числитель дроби = 0, т.е. 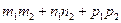=0.

Если прямые L₁ и L₂ параллельны, то параллельны их направляющие векторы S₁ и S₂. следовательно, координаты этих векторов пропорциональны: .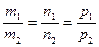

Условие, при котором две прямые лежат в одной плоскости:

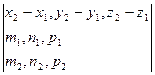=0.

При выполнении этого условия прямые либо лежат в одной плоскости, то есть либо пересекаются.

Взаимное расположение прямой и плоскости.

Угол между прямой и плоскостью. Условия параллельности и перпендикулярности прямой и плоскости.

Пусть плоскость задана уравнением Ах +By + Cz + D=0, а прямая L уравнениями 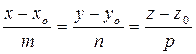. Углом между прямой и плоскостью называется любой из двух смежных углов, образованных прямой и ее проекцией на плоскость. Обозначим через 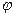угол между плоскостью и прямой.

.

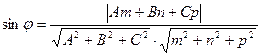Если прямая L параллельна плоскости Q, то векторы n и S перпендикулярны, а потому 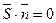, т.е.

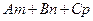=0 является условием параллельности прямой и плоскости.

Если прямая L перпендикулярна плоскости Q, то векторы n и S параллельны. Поэтому равенства

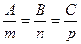являются условиями перпендикулярности прямой и плоскости.

Пересечение прямой с плоскостью. Условие принадлежности прямой плоскости:

Рассмотрим прямую 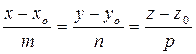и плоскость Ах +By + Cz + D=0.

Одновременное выполнение равенств:

Аm +Bn+ Cp =0

Ах₀+By₀ + Cz₀ + D=0 являются условием принадлежности прямой плоскости.

Эллипс.

Геометрическое место точек, сумма расстояний от которых до двух фиксированных точек плоскости (обычно называемых фокусных) постоянна, называется эллипсом.

Если оси координат расположены так, что Ox проходит через фокусы F₁(C,0) и F₂(-C,0), а О(0,0) совпадает с серед отрезка F₁F₂, то по F₁М+F₂M получаем:

каноническое ур-ие эллипса ,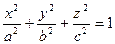

b²=-(с²-a²).

а и b- полуоси эллипса., а-большая, b-меньшая.

Эксцентриситет. 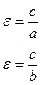, (если а>b)

(если а<b)

Эксцентриситет характеризует выпуклость эллипса.

У эллипса эксцентриситет находится: 0 .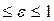

Случай 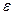=0 возникает только тогда, когда с=0, а это есть случай окружности – это эллипс с нулевым эксцентриситетом.

Директрисы (D) Геометрическое место точек, отношение расстояний от которых до точки эллипса к расстоянию от этой точки эллипса до фокуса постоянно и равно величине 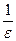, называется директрисами. .

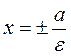Примечание: у окружности нет директрисы.

Гипербола.

Геометрическое место точек, модуль разности расстояний от которых до двух фиксированных точек плоскости постоянна, называется гиперболой.

Каноническое уравнение гиперболы:
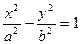, где .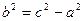

Гипербола есть линия второго порядка.

Гипербола имеет 2 асимптоты: 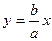и

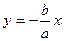
Гипербола называется равносторонней, если ее полуоси равны. (а=b). Каноническое уравнение:

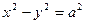
Эксцентриситет – отношение расстояния между фокусами к величине действительной оси гиперболы:

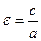
Так как для гиперболы с>а , то эксцентриситет гиперболы >1.

Эксцентриситет характеризует форму гиперболы: 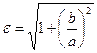. Эксцентриситет равносторонней гиперболы равен равен .

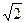Директрисы – прямые .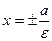

Фокальные радиусы: 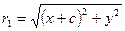и .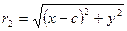

Есть гиперболы, которые имеют общие асимптоты. Такие гиперболы называются сопряженными.

Парабола.

Парабола – множество всех точек плоскости, каждая из которых одинаково удалена от данной точки, называемой фокусом, и данной прямой, называемой директрисой.

Расстояние от фокуса до директрисы – параметр параболы (p>0).-полуфокальный диаметр.

Парабола есть линия второго порядка.

М(х,у) – произвольная точка параболы. Соединим точку М с F, проведем отрезок MN перпендикулярно директрисе. Согласно определению параболы MF=MN. По формуле расстояния между 2 точкам находим: => = =>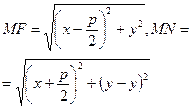

=>

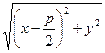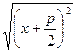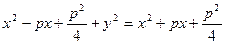Каноническое уравнение параболы:
y² = 2px.

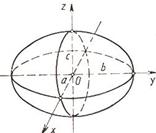
Эллипсоид.

Исследуем поверхность, заданную уравнением:

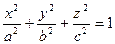
Рассмотрим сечения поверхности с плоскостями, параллельными плоскости xOy. Уравнения таких плоскостей: z=h,где h – любое число. Линия, получаемая в сечении, определяется двумя ур-ниями:

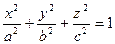
z=h .

Исследуем поверхность:

А) если 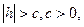то 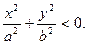Линия пересечения поверхности с плоскостямиz=h не существует.

Б) если 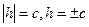, 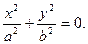линия пересечения вырождается в две точки (0,0,с), и (0,0,-с). Плоскости z = c, z = - c касается данной поверхности.

В) если 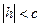, то уравнения можно переписать в виде: 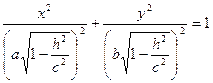, как видно, линия пересечения есть эллипс с полуосями а1 = 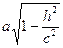, b1 = 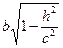. При этом, чем меньше h, тем больше полуоси. При н=0 они достигают своих наибольших значений. а1=а, b1=b. Уравнения примут вид:

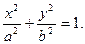
h=0.

Рассмотренные сечения позволяют изобразить поверхность как замкнутую овальную поверхность. Поверхность называется эллипсоидами., если какие-либо полуоси равны, трехосный эллипсоид превращается в эллипсоид вращения, а если а=b=c, то в сферу.

Гиперболоид и конус.

1. Исследуем поверхность 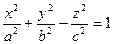.Пересекая поверхностьплоскостью z=h, получим линию пересечения, уравнения которой имеет вид

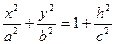
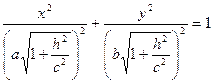
z=h. или z=h

полуоси: а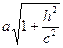1= b1=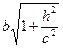

полуоси достигают своего наименьшего значения при h=0: а1=а, b1=b. При возрастании h полуоси эллипса будут увеличиваться. =>

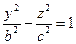
х=0.

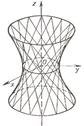
Анализ этих сечений показывает, что поверхность, определяемая уравнением, имеет форму бесконечной расширяющейся трубки. Поверхность называется однополостным гиперболоидом.

2. 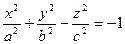-уравнение поверхност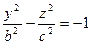и.

и 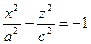-поверхность, состоящая из 2 полостей, имеющих форму выпуклых неограниченных чаш. Поверхность называется двухполостным гиперболоидом.

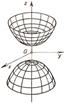
3. Конус второй степени

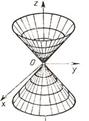Каноническое уравнение:

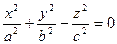
a = b - конус вращения (прямой круговой).

Сечения конуса плоскостями: в плоскости, пересекающей все прямолинейные образующие, - эллипс; в плоскости, параллельной одной прямолинейной образующей, - парабола; в плоскости, параллельной двум прямолинейным образующим, - гипербола; в плоскости, проходящей через вершину конуса, - пара пересекающихся прямых или точка (вершина).
26. Параболоид.

1. 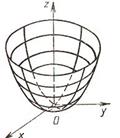-это эллиптический параболоид.

Каноническое уравнение:

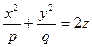(р>0, q>0).

p = q - параболоид вращения вокруг оси Oz.

Сечения эллиптического параболоида плоскостями - либо эллипс, либо парабола, либо точка.

2. 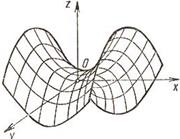- гиперболический параболоид.

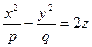
Сечения гиперболического параболоида плоскостями - либо гипербола, либо парабола, либо пара прямых (прямолинейных образующих).