Кирхгофтың екінші заңы бойынша 1 страница

Бірінші бөлім

Сызықты электр тізбектер

Бірінші тарау

1 Тұрақты ток электр тізбектердің негізгі заңдары және есептеу әдістері

1.1 Электр тізбектердің және электр сүлбелердің элементтері

Электр тізбек деп беруге, таратуға және өзара электр энергияны түрлендіруге тағайындалған құрылғылардың жиынтығын атайды.

Электр тізбектердің негізгі элементтері бір-бірімен сымдар арқылы косылған электр энергияның көздері және қабылдағыштары.

Электр энергия көздерінде (аккумуляторлар, электрогенераторлар және т.б) химиялық, механиқалық, жылулық және т.б энергиялар электр энергияға түрлендіреледі, ал электр энергияның қабылдағыштарында электр энергия жылулық, жарықтық, механикалық және т.б энергияға түрлендіреледі.

Токтары және кернеулері уақыт бойынша өзгермейтін тізбектерді тұрақты токтың тізбектері деп атайды.

Токтар және кернеулер тұрақты электр қондырғыларда магнит және электр өрістер уақыт бойынша өзгермейді, сол себептен тұрақты ток тізбектерде өздік индукцияның ЭҚК пайдалы болмайды, ал диэлектриктерде жылжу ток жоқ болады.

Электр сүлбе – электр тізбектің графикалық көрінісі. Ол электр тізбектің элементтерінің қосылуы қалай орындалғанды көрсетеді де,тізбекті есептеуде қолданады.

Сүлбенің екі негізгі элементтері бар: ЭҚК Е және ішкі кедергісі көз (1.1, а - сурет) және қабылдағыштармен сымдардың кедергісі 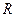(1.1, б - сурет).

Электр қозғаушы күш Е потенциалдардың айырымына немесе көзде ток жоқ кезде болымды 1 және теріс 2 қысқыштардың арасындағы кернеуге тең:

(1.1)

1.1-сурет

Электр қозғаушы күш көздің ішінде кіші потенциялы бар қысқыштан жоғары потенциалы бар қысқышқа болымды зарядтың бірлігін ауыстыруға сыртқы (электр емес) күштердің жұмысы деп белгілеуге болады.

ЭҚК-тің әрекет бағытын сүлбеде тілмен көрсетеді.

Егер электр энергияның көзіне қабылдағышты қосып қойсақ (1.2 - сурет), онда тізбекте ток І пайдалы болады. Бұл жағдайда 1 және 2 қысқыштардағы кернеу ЭҚК-ке тең болмайды, себебі көздің ішінде кернеу түсуі пайда болады, яғни оның ішкі кедергісінде:

Сыртқы сипаттама жүктелген көздің қысқыштарыдағы кернеудің токтан тәуелділігі (1.3 - сурет).

1.2-сурет. Электр тізбек

Энергия көзінің қуаты (1.2)

Қабылдағыштың кедергісі r (1.1, б–сурет) электр сүлбенің элементі ретінде энергияның тұтынуын сипаттайды, яғни қуаты электр энергияны басқа түрге түрлендіреді.

1.3-сурет. Сыртқы сипаттама

Жалпы жағдайда қабылдағыштың кедергісі токтан тәуелді.

Ом заңы бойынша кедергідегі кернеу тең:

(1.4)

Кедергіге кері шама - өткізгіштік деп аталады. Кедергідегі кернеудің токтан тәуелділігі, яғни вольт-амперлік сипаттама деп аталады.

Егер энергия көздерінің ЭҚК-терін, олардың ішкі кедергілерін және

қабылдағыштардың кедергілерін токтардан және кернеулерден тәуелсіз деп

алсақ, онда сыртқы сипаттамалар және вольт-амперлік сипатамалар

сызықты болады (1.4 - сурет).

Тек сызықты сипаттамалары бар элементтерден құралған тізбектер сызықты деп аталады.

1.4 - сурет. Сызықты сипаттамалар

1.2 Энергия көздерінің балама сұлбалары

Белгілі ЭҚК Е және ішкі кедергісі бар энергия көзін балама сұлбамен көрсетуге болады.

Жоғарыда көрсетілгендей көздің қысқыштарындағы кернеу

(1.5)

Басқа жағынан , 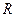кедергідегі кернеу

(1.6)

болғандықтан немесе

(1.7)

(1.7) теңдеуден табамыз

(1.8)

Бұдан көздің ішкі кедергісі қабылдағыштың кедергісі сияқты токты шектейтіні көрініп тұр.

1.5, а-суретте балама сұлбаның Е ЭҚК-і бар көзі кезінде U кернеу қабылдағыштың тоғына тәуелді де тең . Егер де Ri<<R болса, онда Ui<<U болады да ішкі кернеу түсуді еске алмай (Ui=RiI=0) 1.5, б-суреттегі балама сұлбаны алуға болады. Мұндай ішкі кедергісі жоқ энергия көзін, тілі бар дөңгелекпен белгілейміз және қасына Е әріпті жазамыз да, өте оңды ЭҚК-тің көзі деп атаймыз. Оның сыртқы сипаттамасы - абсцисс білікке параллельді тура сызық (1.3-суреттегі ав штрих тура сызық).

а) б)

1.5 - сурет. Энергия көздерінің балама сұлбалары:

а - көздің ішкі кедергісін есепке алғанда;

б - көздің ішкі кедергісін есепке алмағанда.

Энергия көзін екінші балама сұлбамен көрсетуге болады (1.6, а-сурет ).

(1.7) теңдеудің оң және сол жағын кедергіге бөлсек, шығады

(1.9)

мұндағы -энергия көзінің ішкі өткізгіштігі.

(1.10)

мұндағы - көздің қысқа тұйықталған кездегі ток, яғни R=0 кездегі ток; - энергия көзінің шықпаларындағы кернеудің оның ішкі кедергісіне қатынасына тең ток. - қабылдағыштық тоғы.

а) б)

1.6 - сурет. Энергия көздерінің балама сұлбалары:

а - көздің ішкі өткізгіштігін есепке алғанда;

б - ішкі өткізгіштігін есепке алмағанда.

(1.10) теңдеуге тапсырылған тоғы бар көзден және онымен паралельді қосылған R_i элементтен кұрылған ток көзінің балама сұлбасы қанағат болады. (1.6, а - сурет).

Егер R_i >> R немесе << болса, онда ток << , яғни энергия көзі қысқа тұйықталу ережеге жақын болады. Бұл жағдайда деп алып энергия көзі тек ток көзі бар балама сұлба шығады (1.6, б-сурет).

Ішкі өткізгіштегі көз екі тілі бар дөңгелекпен белгілейміз және қасына J әріпті жазамыз да, өте оңды токтың көзі деп атаймыз. Өте оңды ток көзінің тоғы қабылдағыштың R кедергісіне тәуелсіз. Оның сыртқы сипаттамасы-ординат білікке параллельді тура сызық (1.3-суреттегі св штрих тура сызық).

ЭҚК - тердің көзі активтік, ал кедергілер пассивтік электр сұлбалардың элементтеріне жатады.

1.3 ЭҚК-і бар тізбек бөлігі үшін Ом заңы

Тармақталмаған құранды сүлбенің (1.7-сурет) бөлігінің тоғы үшін, еркінше ЭҚК-тері және кедергілері болғанда, егерде аяқтарындағы потенциалдар айырымы белгілі болса жазуға болады:

(1.11)

1.7 - сурет. Кұрамды сүлбенің бөлігі.

Егер токтың бағыты алдын-ала белгісіз болса, онда токтың бағытын еркінше таңдаймыз. Мұндай еркінше таңдалған токтың бағытын болымды деп атайды.

(1.9) теңдеуден шығады:

(1.12)

мұнда - бөліктің қосынды кедергісі;

- потенциалдардың айырымы немесе бөліктің қысқыштар арасындағы кернеу;

- бөлікте әрекет ететін ЭҚК-терден алгебралық қосындысы.

(1.12) кейіптеме - ЭҚК-тері бар тізбектің бөлігі үшін Ом заңы.

Егер (1.12) кейіптемемен есептегенде ток I теріс болып шықса, онда токтың нақтылы бағыты алынған болымды бағытпен беттеспейді.

1.4 Тармақталмаған электр тізбекті бойлай потенциалдардың таратылуы

Тармақталмаған электр тізбекті бойлай потенциалдардың таралуын көрнекті түрде график арқылы көрсетуге болады. 1.8-суретте тармақталмаған тізбектің сүлбесі көрсетілген.

ЭҚК мәні ЭҚК мәнінен үлкен деп алайық. Бұл жағдайда нақтылы ток тең, ал бағыты ЭҚК -дің бағытымен бірдей.

нүктенің потенциалы деп алғанда нүктенің потенциалы тең болады: .

Бірінші энергия көзінен өткенде потенциал мәніне өседіде ішкі кедергіде азаяды, сонымен с нуктенің потенциалы тең

.

1.8 - сурет. Тармақталмаған

тізбектің сүлбесі

d нүктенің потенциалын табу үшін потенциалдан кернеу түсуді алу керек, яғни .

Ақырында, екінші энергияның көзінен өткен кезде потенциал ЭҚК мәніне және ішкі кедергі кернеу түсуіне азаяды, ал сонымен бірге, а нүктенің потенциалы нөлге тең болу керек:

.

Егер де абсцисс білігінде таңдалған кедергінің масштабында тізбекке қосылған бөліктерінің кедергілерін, ал ординат білігінде сәйкесті нүктелердің потенциалдарын салсақ, онда тармақталмаған тізбектің потенциалдық таратылу графигі шығады (1.9 - сурет).

Графикті пайдаланып тізбектің кандай да болған нүктелерінің арасындағы кернеуін табуға болады. Мысалы, бірінші көздің қысқыштарындағы кернеу

.

Тізбек бойы ток І тұрақты, яғни барлық участіктерде бірдей болғандықтан ол графикте абсцисс білікке сәйкесті тұра сызықтың еңкеюi бұрыштық тангенсына тең, яғни тұра сызыктардың еңкеюi бірдей (мысалы, “а в” және “с d”).

1.9 - сурет. Тармақталмаған тізбекті бойлай потенциалдардың тарауы.

1.5 Тармақталмаған тізбек үшін қуаттардың тепе-теңдігі

ЭҚК -і және ішкі кедергісі бар тұрақты ток электр генераторы және ЭҚК-і және ішкі кедергісі бар аккумулятордан құралған электр тізбек үшін (1.10-сурет) энергетикалық катынасты қарап шығайық. Генератордың ЭҚК- аккумулятордың ЭҚК-інен үлкен, яғни аккумулятор зарядталып тұр. Бұл жағдайда токтың нақтылы бағыты ЭҚК -мен біртектес.

Генератордың шықшықтарындағы кернеу

(1.13)

Аккумулятордың шықшықтарындағы кернеу

(1.14)

1.10 - сурет. Тұрақты ток генератордан және аккумулятордан құралған электр тізбектің сүлбесі.

(1.12) теңдеудің екі бөлігін І токқа көбейтіп және қосындыларды орын алмастырып табамыз

. (1.15)

Бұл теңдеудің сол жағы генератордың өндеген қуаты; оң жағының бірінші қосындысы - генератордың орамасындағы жылулық шығындарының қуаты, екінші қосынды - аккумулятордың тұтынатын қуаты.

Егер де (1.13) теңдеудің сол және оң жағын токқа көбейтсек, онда болады:

. (1.16)

Бұл теңдеуден шығады: аккумулятордың тұтынған қуаты U I жылулық шығындарға ( ) және аккумуляторды зарядтауға кетеді.

Энергия сақтау заң бойынша энергия көздерінің қуаттар қосындысы кедергілерде шығындалатын қуаттар қосындысына тең, яғни

. (1.17)

Егер де ЭҚК Е және ток І бағыттары біртектес болса, онда қуат болымды болып алынады, егер де ЭҚК және тоқтың бағыттары бір-біріне қарсы, онда қуат теріс болады. Мысалы, .

1.6 Тармақталған тізбектерді есептеу үшін Кирхгофтың заңдарын қолдану

Тізбектеп қосылған ЭҚК-тердің көздерінен және кедергілерден құралған электр тізбектің бөлігі тармақ деп аталады.

Үш және одан көп тармақтардың қосылған орыны (нүктесі) электр тізбектің түйіні деп аталады.

Бірнеше тармақтардан өтетін тұйықталған жол электр тізбектің контуры деп аталады. Сонымен бірге қаралып тұрған контурда әрбір түйін бірақ рет кездеседі. Қандай да болған кескін үйлесімі бар электр тізбектің ережесі Кірхгофтың бірінші және екінші заңдарымен толық белгіленеді.

Кирхгофтың бірінші заңы:

Түйінде тоқтардың алгебралық қосындысы нөлге тең, яғни

(1.18)

Бұл теңдеуде түйінге бағытталған токты теріс таңбамен, ал түйіннен бағытталған токты болымды таңбамен жазамыз

Кирхгофтың екінші заңы:

Қандай да болған тұйықталған контурда осы контурға кіретін кедергілердегі кернеулердің алгебралық қосындысы сол контурға кіретін ЕҚК-тердің алгебралық қосындысына тең (1.19)

Бұл теңдеуде токтардың және ЭҚК-тердің болымды таңбалары қаралып тұрған контурды еркінше таңдалған айналма жолдың бағытымен біртектес болғанда алынады.

Егер де тізбектің элементтерінің параметрлары және оның кескін үйлесімі белгілі болса, ал токтарды табу керек болса, онда Кирхгоф заңдары бойынша теңдеулерді құрған кезде мынадай тәртіп болу керек:

- электр тізбектің барлық тармақтарында токтың ерекше болымды бағыттары таңдалады;

- кирхгофтың бірінші заңы бойынша контурлар үшін теңдеулер құрылады;

- кирхгофтың екінші заңы бойынша контурлар үшін теңдеулер құрылады.

Электр тізбектің в тармағы және у түйіні болсын.

Кирхгофтың бірінші және екінші заңдары бойынша сәйкесті у- 1 және в-у+1 өзара тәуелсіз теңдеулерді құруға болады. Бұл теңдеулердің

қосындысы керекті және жеткілікті в тармақтардағы барлық токтарды белгілеу үшін теңдеулер санын береді.

Мысалы, 1.11-суреттегі төрт түйіні бар электр тізбек үшін Кирхгофтың бірінші заңы бойынша теңдеулердің түрі:

1 түйін үшін ;

2 түйін үшін ; (1.20)

3 түйін үшін ;

4 түйін үшін ;

Бұл теңдеулердің қосындысы 0=0 тепе-теңдікті береді, яғни төрт теңдеуден тек үшеу тәуелді.

Барлық теңдеулер саны в тармақтардың санына тең болу керек.

Бірінші заң бойынша у-1 теңдеу саны болғандықтан, екінші заң бойынша в-у+1 теңдеу саны болу керек. 1.11-суреттегі сұлба үшін Кирхгофтың екінші заңы теңдеу саны в-у+1=6-4+1=3.

1-4-2-1 контур үшін ;

1-3-4-1 контур үшін ; (1.21)

2-4-3-2 контур үшін .

(1.20) және (1.21) теңдеулерді бірлесіп шешкен кезде 1.11-суретте көрсетілген электр тізбектің барлық тармақтардағы токтардың шамаларын береді.

1.7 Түйінді потенциалдар әдісі

Кирхгофтың бірінші заңын және Ом заңын қолдануға негізделген түйіндік потенциалдар әдісін пайдалансақ шешүге жататын теңдеулердің санын қысқартуға болады. 3 нүктенің потенциалын нөлге тең деп алайық. Таңдалған болымды бағыттары бойынша 1 және 2 түйіндер үшін Кирхгофтың бірінші заңы бойынша жазамыз:

(1.22)

Тармақтардағы токтар Ом заңы бойынша:

(1.23)

1.12 - сурет

(1.22) теңдеулерді (1.21) теңдеулерге қойып және олардың мүшелерін топтағаннан кейін табылады:

(1.24)

немесе

(1.25)

Бұл теңдеулерде - сәйкесті 1 және 2 түйіндерін қосылған тармақтардың өткізгіштердіктің қосындысы: - бұл түйіндерді қосатын тармақтардың өткізгіштердің қосындысы.

(1.24) теңдеулер тармақтардағы токтардың таңдалған болымды бағыттарына тәуелді емес.

Егер де тізбекте екі ғана түйін, ол параллельді қосылған тармақтардың саны m болса, онда түйіндер арасындағы кернеуді табуға болады (1.13-сурет).

1 түйін үшін (1.24) теңдеуді құрамыз

(1.26)