Раздел II. Случайные величины
Тема 3. Случайные величины.Математическое ожидание и дисперсия дискретной случайной величины.
Случайная величина. Функция распределения дискретной случайной величины. Типичные законы распределения непрерывных случайных величин. Числовые характеристики случайных величин. Числовые характеристики типичных случайных величин. Ковариация и коэффициент корреляции. Линейная регрессия.
Тема 4. Нормальное и показательное распределение.
Генеральная совокупность и выборка. Первичная обработка данных. Определение параметров закона распределения. Доверительные интервалы. Проверка статистической гипотезы. Критерии согласия Пирсона.
Раздел III. Элементы математической статистики
Тема 5. Элементы математической статистики. Выборочный метод. Статистические оценки параметров распределения. Элементы теории корреляции.
Задачи математической статистики. Генеральная и выборочная совокупности. Повторная и бесповторная выборки. Репрезентативные выборки. Статистическое распределение выборки. Статистические оценки параметров распределения. Генеральная средняя. Выборочная средняя. Дисперсии, их виды и способы вычисления. Точечные оценки. Доверительные интервалы. Метод расчёта сводных характеристик выборки. Элементы теории корреляции. Статистическая проверка статистических гипотез. Критерий согласия Пирсона.
Перечень вопросов, отводимых студентам на самостоятельное изучение
1. Вероятностное пространство. Аксиомы теории вероятностей.
2. Теорема Ляпунова. Центральная предельная теорема.
3. Распределение Стьюдента. Распределение Фишера-Снедекора.
4. Корреляционный момент. Коэффициент корреляции.
5. Корреляционная таблица. Выборочный коэффициент корреляции.
6. Выборочное корреляционное отношение.
7. Простейшие случаи криволинейной корреляции.
8. Понятие о множественной корреляции.
9. Статистическая гипотеза. Нулевая и конкурирующая, простая и сложная гипотезы.
10. Возможные ошибки первого и второго рода при проверке статистической гипотезы.
11. Критерий согласия Пирсона. Критерий Бартлетта. Критерий Уилкоксона.
12. Комплексные случайные величины и функции, их характеристики.
13. Стационарные случайные функции.
14. Понятие о спектральной теории стационарных случайных функций.
Лекции по дисциплине
Теория вероятностей и математическая статистика».
Лекция 1. Введение. Случайные события.
Основные понятия теории вероятностей.
ПРЕДИСЛОВИЕ
Теория вероятностей – раздел математики, в котором даются способы подсчёта вероятности случайных событий и рассматриваются случайные величины.
Термины «вероятность», «событие», «случайная величина», будут разъясняться по мере прохождения курса. Методы теории вероятностей применяются в экономике, биологии, физике и в других областях. В нефтяном деле можно по исходным данным определять вероятность залегания нефтесодержащих пластов в каком-либо районе, определять вероятность того, что оборудование проработает определённое время.
1. СОБЫТИЕ, ОПЫТ
Опыт (эксперимент, испытание) – действие (или действия) с целью выяснить, произойдёт или не произойдёт интересующий вас результат.
Любой результат опыта (возможный либо уже осуществившийся) называется событием.
Пример: вы подбрасываете монету 9 раз, чтобы посмотреть, выпадет ли герб 3 раза.
Подбрасывание монеты 9 раз есть опыт. Выпадение при этом герба 5 раз и решки 4 раза – событие.
В теории вероятностей имеют дело с опытами:
- которые можно воспроизводить мысленно или реально любое число раз;
- результаты которых заранее непредсказуемы.
Повторяя такой опыт, вы заметите, что одни события могут происходить часто, другие – редко. Иными словами, одни события более вероятны, другие – менее вероятны. Следовательно, вероятность есть величина, дающая представление о частоте события. Точное определение вероятности, позволяющее вычислять её, дано в разделе 3.
2. ТИПЫ СОБЫТИЙ
Приведём названия событий, с которыми придётся иметь дело.
Достоверное событие (  ) –которое в опыте обязательно произойдёт.
) –которое в опыте обязательно произойдёт.
Невозможное событие (  ) –которое в опыте обязательно не произойдёт.
) –которое в опыте обязательно не произойдёт.
Случайное событие (  ) –в опыте не обязательно должно произойти.
) –в опыте не обязательно должно произойти.
Таким образом, случайное событие непредсказуемо: оно может произойти, но может и не произойти.
Пример: вы подбрасываете два игральных кубика. Тогда
 выпадет двузначное натуральное число (достоверное событие);
выпадет двузначное натуральное число (достоверное событие);
 выпадет число 67 (невозможное событие);
выпадет число 67 (невозможное событие);
 выпадет двузначное число, делящееся на 4 (случайное событие).
выпадет двузначное число, делящееся на 4 (случайное событие).
Два случайных события или больше называются несовместными в данном опыте, если осуществление любого из них означает неосуществление остальных.
Пример: вы подбрасываете два игральных кубика и вас интересуют следующие события:  выпадет чётная сумма очков,
выпадет чётная сумма очков,  выпадет число 31,
выпадет число 31,  выпадет число 32. Здесь события
выпадет число 32. Здесь события  и
и  совместны (появление
совместны (появление  не исключает появления
не исключает появления  т. е. события
т. е. события  и
и  могут появиться вместе), но события
могут появиться вместе), но события  и
и  (а также
(а также  и
и  ) несовместны.
) несовместны.
Два случайных события или больше называются равновозможными в данном опыте, если ни одно из них не имеет предпочтения перед другими.
Пример: при однократном бросании кубика события 1, 2, 3, 4, 5, 6 равновозможны (если кубик правильный: все грани одинаковы и центр тяжести не смещён).
3. КЛАССИЧЕСКАЯ ФОРМУЛА ВЕРОЯТНОСТИ
Несовместимые друг с другом равновозможные результаты опыта называются равновероятными исходами или шансами.
Например, при подбрасывании кубика каждый возможный результат 1, 2, 3, 4, 5, 6 есть шанс.
Обычно шансы обозначаются символами 
Если осуществление шанса  приводит к появлению события
приводит к появлению события 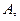 то
то  называется благоприятным шансом для события
называется благоприятным шансом для события  .
.
Пример: вы один раз подбрасываете кубик и вас интересует событие выпадет чётное число. Тогда благоприятными для события
выпадет чётное число. Тогда благоприятными для события  будут шансы
будут шансы 


Пусть событию  благоприятствуют
благоприятствуют  шансов из
шансов из  возможных. Тогда
возможных. Тогда
Вероятностью события  называется число называется число  определяемое по формуле определяемое по формуле |
  |
(3.1)
Это классическая формула вероятности.
Так как 
 то
то  и по формуле (3.1) получим
и по формуле (3.1) получим
 |
Рассмотрим два крайних случая.
Если  невозможное событие, то шансов, благоприятных для
невозможное событие, то шансов, благоприятных для 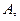 не существует, поэтому
не существует, поэтому 

Если  достоверное событие, то каждый из
достоверное событие, то каждый из  шансов благоприятен для
шансов благоприятен для 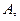 поэтому
поэтому 

З а д а ч а 1. Вы один раз подбрасываете кубик. Какова вероятность появления числа, делящегося на 3?
■ При одном бросании может выпасть любое число от 1 до 6. Поэтому число шансов 
Событию  появится число, делящееся на 3, благоприятствуют 2 шанса:
появится число, делящееся на 3, благоприятствуют 2 шанса:  и
и  поэтому
поэтому  Следовательно, вероятность события
Следовательно, вероятность события  равна
равна
 ■
■
Подсчёт вероятности по классической формуле можно проводить, последовательно отвечая на следующие вопросы:
1) Какой опыт осуществляется?
2) Назовите какой-либо возможный исход (шанс).
3) Посчитайте количество  всех возможных шансов.
всех возможных шансов.
4) Какое событие вас интересует?
5) Посчитайте количество  шансов, благоприятствующих этому событию.
шансов, благоприятствующих этому событию.
З а д а ч а 2. Вы подбрасываете монету 3 раза. Найдите вероятность появления хотя бы одного герба.
□ 1) Осуществляется опыт: монета подбрасывается 3 раза.
2) Один из возможных исходов трёх бросаний: герб, герб, число (ггч).
3) Шансы: {ггг, ггч, гчг, чгг, гчч, чгч, ччг, ччч}. Всего  шансов.
шансов.
4) Интересуемся событием  появится хотя бы один герб.
появится хотя бы один герб.
5) Этому событию благоприятствуют  шансов (в пункте 3 они подчёркнуты).
шансов (в пункте 3 они подчёркнуты).
6) Вероятность этого события  ■
■
4. ПОДСЧЁТ ЧИСЛА ШАНСОВ
Когда число шансов велико, их перебор становится трудоёмким занятием. Рассмотрим два правила, помогающие находить значения  и
и  Они основаны на том, что число шансов
Они основаны на том, что число шансов  числу способов осуществить нужные действия.
числу способов осуществить нужные действия.
Введём следующие обозначения:
 число способов выполнить действие
число способов выполнить действие 
 число способов выполнить
число способов выполнить  при условии, что
при условии, что  уже выполнено.
уже выполнено.
Тогда
 | Правило сложения |
 | Правило умножения |
З а д а ч а 1. В первом ящике 30 яблок, во втором 40 груш, в третьем 50 лимонов. Вы берёте 1 плод. Сколько существует способов выбрать яблоко или лимон?
□ Введём следующие события: Я = берётся яблоко, Л = берётся лимон.
Эти действия несовместны, поэтому

 способов. ■
способов. ■
З а д а ч а 2. Сколько существует способов рассадить 3 человек на 4 стульях?
□ Пусть П = вы усаживаете на какой-либо стул первого человека;
В = затем усаживаете второго человека на какой-либо незанятый стул;
Т = затем усаживаете третьего человека на какой-либо незанятый стул.
Тогда 
 способа. ■
способа. ■
З а д а ч а 3. Сколько существует способов расставить на пустой полке книги А, В, С?
□ Пусть П = вы ставите на первое место какую-либо книгу;
В = затем ставите на второе место какую-либо из оставшихся книг;
Т = затем ставите на 3-е место оставшуюся книгу.
Тогда 
 способов. ■
способов. ■
И вообще,
число всевозможных способов расставить  элементов
элементов  .
.
5. СОЧЕТАНИЯ
Пусть вы имеете  различных элементов.
различных элементов.
Из них вы отбираете  штук, поэтому
штук, поэтому 
Набор элементов, взятых из какого-то множества, называется сочетанием, если не нужно учитывать, в какой последовательности (в каком порядке) брались элементы.
Следовательно, сочетание – это подмножество какого-то множества.
Число способов выбрать всевозможные  элементные сочетания обозначается
элементные сочетания обозначается  и вычисляется по формуле
и вычисляется по формуле


Символ  читается как «число сочетаний
читается как «число сочетаний  из
из  ».
».
З а д а ч а 1. Найти число способов выбрать 3 дежурных в группе из 25 человек.
□ Здесь не нужно учитывать, в каком порядке выбираются 3 человека, поэтому
 способов. ■
способов. ■
З а д а ч а 2. В ящике 8 яблок и 7 груш. Наугад берут 6 плодов. Какова вероятность того, что попадутся 4 яблока и 2 груши?
□ Здесь не нужно учитывать порядок, поэтому применяем сочетания.
Из всего множества  берутся
берутся  плодов,
плодов,

поэтому число всевозможных исходов

Вас интересует событие  где
где  берутся 4 яблока,
берутся 4 яблока,  берутся 2 груши.
берутся 2 груши.
4 яблока берутся из имеющихся 8 яблок, а 2 груши – из имеющихся 7 груш:

поэтому число благоприятствующих исходов

Отсюда
 ■
■
6. СТАТИСТИЧЕСКАЯ ФОРМУЛА ВЕРОЯТНОСТИ
Вообразите, что вы бросаете мяч в корзину, чтобы узнать свою меткость. Для этого вы сделали, скажем, 20 бросков и получили такие результаты:
| Номер броска | 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
 попадание в цель попадание в цель | + + + + + + + + + + + + + |
Вы 13 раз попали в корзину. Число  называется относительной частотой попаданий. Это число вы можете принять за вероятность попадания при 1 броске. Оно оценивает вашу меткость: чем ближе это число к 1, тем больше меткость.
называется относительной частотой попаданий. Это число вы можете принять за вероятность попадания при 1 броске. Оно оценивает вашу меткость: чем ближе это число к 1, тем больше меткость.
Относительной частотой события  или статистической вероятностью события или статистической вероятностью события  называется число называется число  определяемое по формуле определяемое по формуле |
  |
Так, наблюдения за рождением детей показали, что статистическая вероятность рождения мальчика равна 
7. ГЕОМЕТРИЧЕСКАЯ ФОРМУЛА ВЕРОЯТНОСТИ
 Вообразите, что вы наугад бросаете крупинку в область
Вообразите, что вы наугад бросаете крупинку в область  (рис. 7.1). Какова вероятность того, что она упадёт на участок
(рис. 7.1). Какова вероятность того, что она упадёт на участок  этой области?
этой области?
Справедливо следующее утверждение.
Если равновозможно попадание наудачу брошенной крупинки в любую точку области  , , |
то вероятность того, что она упадёт на участок  равна равна  |
Рис. 7.1
В этой формуле участвуют геометрические величины – площади, отсюда и название: геометрическая формула вероятности.

Аналогично определяется вероятность, когда вы бросаете
крупинку на отрезок  или в объём
или в объём 
З а д а ч а 1. На плоскости начерчены две концентрические окружности радиусом 5 и 10 см (рис. 7.2). Найти вероятность того, что песчинка, брошенная на большой круг  попадёт в кольцо
попадёт в кольцо 
□  ■Рис. 7.2
■Рис. 7.2
8.ДЕЙСТВИЯ НАД СОБЫТИЯМИ
Имея какие-либо события, вы можете получать новые события.
1. Если дано событие 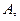 то противоположным ему будет событие
то противоположным ему будет событие  означающее, что
означающее, что  не произойдёт:
не произойдёт:
 событие событие  не появится. не появится. |
Например, если  при выстреле вы попадёте в цель, то
при выстреле вы попадёте в цель, то  вы промахнётесь.
вы промахнётесь.
 Из двух событий
Из двух событий 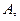
 одно обязательно произойдёт, они дополняют друг друга. События
одно обязательно произойдёт, они дополняют друг друга. События 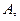
 несовместны. Символ
несовместны. Символ  есть знак отрицания.
есть знак отрицания.
Пусть среди всех  возможных шансов событию
возможных шансов событию  благоприятствуют
благоприятствуют  шансов (на рис. 8.1 они изображены крас- Рис. 8..1
шансов (на рис. 8.1 они изображены крас- Рис. 8..1
ными кружками). Тогда остальные шансы будут благоприят-
ны противоположному событию  их количество
их количество

 (8.1)
(8.1)
2. Пусть теперь имеются два события 

Тогда вы можете создать новое событие 
 события события  произойдут вместе, совместно. произойдут вместе, совместно. |
Событие  называется произведением этих событий и обозначается ещё так:
называется произведением этих событий и обозначается ещё так: 
Например, если  наудачу вызванный студент умеет играть на баяне,
наудачу вызванный студент умеет играть на баяне,
 наудачу вызванный студент умеет хорошо петь,
наудачу вызванный студент умеет хорошо петь,
то  наудачу вызванный студент играет на баяне и хорошо поёт.
наудачу вызванный студент играет на баяне и хорошо поёт.
События 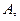
 несовместны, поэтому событие
несовместны, поэтому событие  невозможно:
невозможно:

 Пусть событию
Пусть событию  благоприятны шансы, изображённые на рис. 8.2 кружками, содержащими красный цвет, а событию
благоприятны шансы, изображённые на рис. 8.2 кружками, содержащими красный цвет, а событию  благоприятны шансы, изображённые кружками, содержащими синий цвет. Тогда событию
благоприятны шансы, изображённые кружками, содержащими синий цвет. Тогда событию  будут благоприятны шансы, изображаемые кружками, содержащими и красный и синий цвет, т. е. событию
будут благоприятны шансы, изображаемые кружками, содержащими и красный и синий цвет, т. е. событию  соответствует пересечение множеств
соответствует пересечение множеств 
 Рис. 8.2
Рис. 8.2
3. Пусть снова имеются два события 
 Тогда вы можете ввести новое событие
Тогда вы можете ввести новое событие 
 произойдёт хотя бы одно из этих событий. произойдёт хотя бы одно из этих событий. |
 Это значит, что произойдёт не меньше одного события: либо только
Это значит, что произойдёт не меньше одного события: либо только 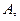 либо только
либо только  либо произойдут
либо произойдут  вместе (рис. 8.3). Событию
вместе (рис. 8.3). Событию  соответствует объединение множеств. Событие
соответствует объединение множеств. Событие  называется суммой этих событий и обозначается ещё так:
называется суммой этих событий и обозначается ещё так: 
Например, если  наудачу вызванная студентка является хохотушкой,
наудачу вызванная студентка является хохотушкой,  наудачу вызванная студентка любит пирожные, то
наудачу вызванная студентка любит пирожные, то  наудачу вызванная студентка либо хохотушка, либо любит пирожные, либо является хохотушкой, любящей пирожные. Рис. 8.3
наудачу вызванная студентка либо хохотушка, либо любит пирожные, либо является хохотушкой, любящей пирожные. Рис. 8.3
Заметим, что фразы:
«хотя бы одно»,
«по меньшей мере, одно»,
«по крайней мере, одно»,
«не меньше одного»,
«одно или больше»
являются равносильными, означающими одно и то же.
Рис. 8.3 показывает, что количество шансов, благоприятных для события  определяется равенством
определяется равенством
 (8.2)
(8.2)
Из двух событий 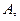
 одно обязательно произойдёт, поэтому событие
одно обязательно произойдёт, поэтому событие  достоверно:
достоверно:

Операции  обладают следующими свойствами:
обладают следующими свойствами:
 |
 |
 |
(8.3)
(8.4)
9. ВЕРОЯТНОСТЬ ПРОТИВОПОЛОЖНОГО СОБЫТИЯ
Вероятность события  противоположного событию противоположного событию 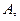 определяется по формуле определяется по формуле |
 |
(9.1)
¨ Эта формула получается из (8.1) путём деления обеих частей на  ■
■
З а д а ч а 1. Какова вероятность вытащить из колоды в 36 карт не туза?
□ Первый способ. В колоде 4 туза, поэтому вероятность события  равна
равна

Находим вероятность противоположного события 

Второй способ. Количество не тузов в колоде равно  поэтому вероятность вытащить не туза равна
поэтому вероятность вытащить не туза равна
 ■
■
Вопросы к экзамену
1.Предмет теории вероятностей. Понятие случайного события.
2.Виды случайных событий. Несовместные, достоверные и невозможные события.
3.Относительная частота событий. Статистическая вероятность.
4.Аксиомы теории вероятностей и следствия из них.
5.Классическое определение вероятности. Свойства вероятности.
6.Основные понятия и формулы комбинаторики. Примеры непосредственного вычисления вероятностей.
7.Теорема сложения вероятностей.
8. Лекция 2. Теорема сложения и умножения вероятностей
