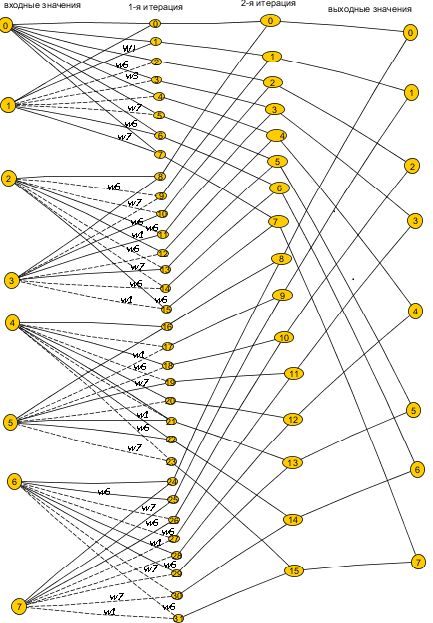
Граф вычислительного процесса

A*b

B*a

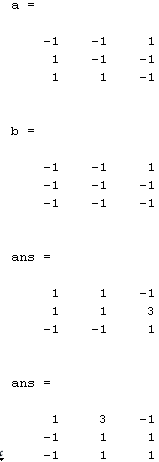
Вычислить кронекеровское произведение усеченных матриц:

>> kron(a,b)

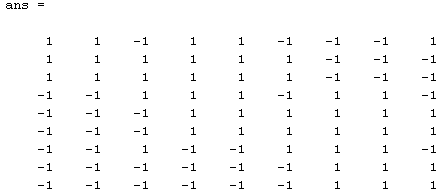
Задание 2. Анализ и формализация типовых задач цифровой обработки.

Представить формализацию задачи декодирования для полученной ранее бинарной матриц и строки, указанной в задании 2 (строка 1) методом максимального правдоподобия:

Счет строк ведем с 0.

Умножим матрицу кодовых слов А(i) на слово, соответствующий первой строке

этой же матрицы.

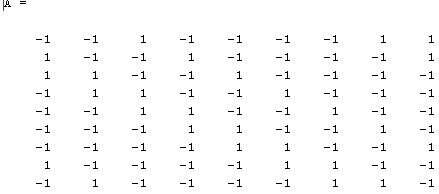
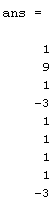
Первая компонента выходного вектора является максимальной, следовательно

нами было принято первое слово.

Представить формализацию задачи синхронизации кода, полученного на основе циркулянта строки кода Баркера длины N=13 и кодового слова с номером согласно варианта (строка 2):

Счет строк ведем с 0.

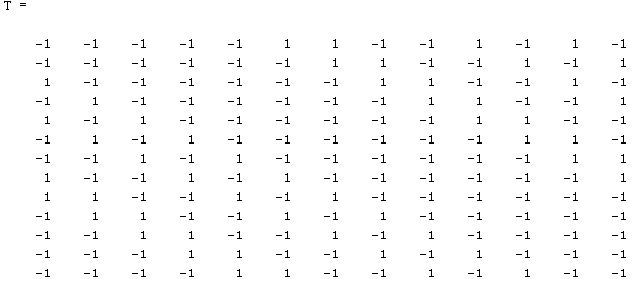
T3=T(3,1:end)'

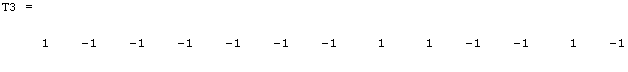
T*T3'

Одиннадцатая компонента выходного вектора максимальна, следовательно сигнал

смещён на 11 тактов.

Представить формализацию задачи обнаружения фрагмента изображения на основе матричной алгебры для пиксельного изображения соответствующего циркулянту задания 1 (крест из1 размером 3*3):

Для обнаружения изображения используется поэлементное сравнение изображения с образцом.

>> C = [-1 1 -1;

1 1 1;

-1 1 -1]

>> K = [];

>> for i = 1:7

for j = 1:7

Y = A(i:i+2, j:j+2);

k = C.*T;

K(i,j) = sum(sum(k));

End

End

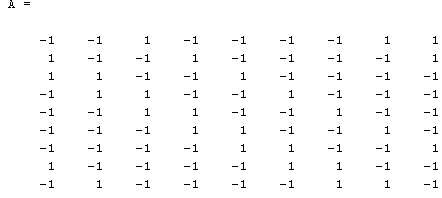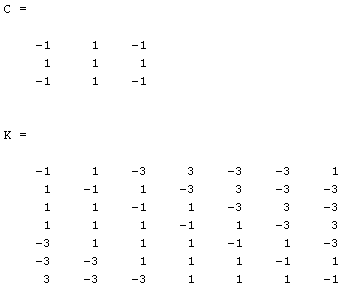
Максимальный уровень корреляции 3, следовательно совпадений нет и

искомое изображение не обнаружено

Задание 3. Факторизация бинарных матриц и преобразования Адамара

3-1.Построить матрицу Адамара третьего порядка, осуществить ее факторизацию

двумя способами, представить граф вычислительного процесса умножения вектора на матрицу, провести анализ вычислительной сложности:

Счет строк ведем с 0.

1 1 1 1 1 1 1 1 1 -1 1 -1 1 -1 1 -1 1 1 -1 -1 1 1 -1 -1 1 -1 -1 1 1 -1 -1 1 1 1 1 1 -1 -1 -1 -1 1 -1 1 -1 -1 1 -1 1 1 1 -1 -1 -1 -1 1 1 1 -1 -1 1 -1 1 1 -1

Строим матрицу Адамара третьего порядка:

-1

-1

-1

=

Получить матрицу Адамара 3-го порядка можно кронекеровски перемножив три матрицы Адамара первого порядка.

Согласно теореме матрица А раскладывается на произведение трех слабо заполненных сомножителей:

А=В₃*В₂*В₁=В³ , где

>> А = hadamard(8)   А =   1 1 1 1 1 1 1 1 1 -1 1 -1 1 -1 1 -1 1 1 -1 -1 1 1 -1 -1 1 -1 -1 1 1 -1 -1 1 1 1 1 1 -1 -1 -1 -1 1 -1 1 -1 -1 1 -1 1 1 1 -1 -1 -1 -1 1 1 1 -1 -1 1 -1 1 1 -1

Граф вычислительного процесса.

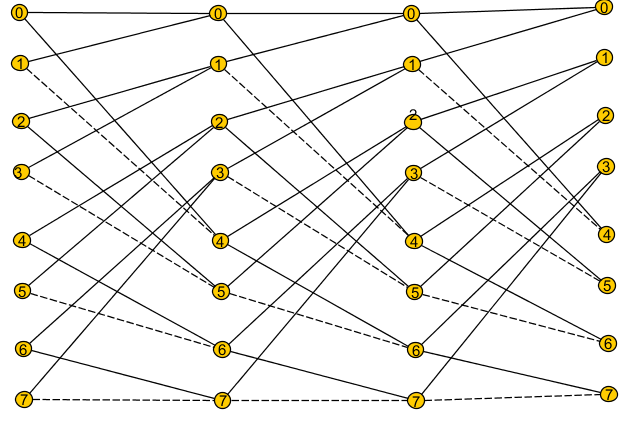
Согласно теоремы 2 факторизовать матрицу Адамара можно по формуле:

из этого следует:

>> А = hadamard(8)

А =

1 1 1 1 1 1 1 1

1 -1 1 -1 1 -1 1 -1

1 1 -1 -1 1 1 -1 -1

1 -1 -1 1 1 -1 -1 1

1 1 1 1 -1 -1 -1 -1

1 -1 1 -1 -1 1 -1 1

1 1 -1 -1 -1 -1 1 1

1 -1 -1 1 -1 1 1 -1

Граф вычислительного процесса

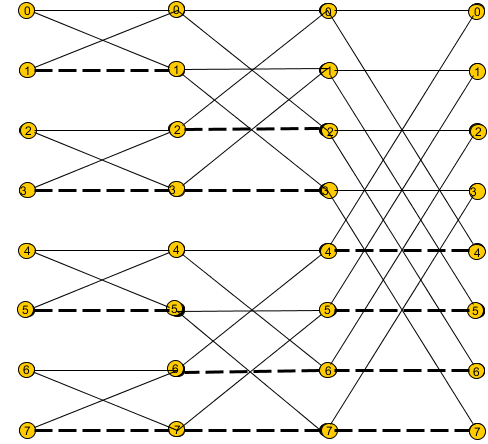
Анализ вычислительной сложности

3-2.Используя матрицу-циркулянт из первого задания разработать алгоритм ее факторизации на основе универсального метода, построить граф вычислительного процесса векторно-матричного произведения и проверить результат, провести анализ вычислительной сложности.

Счет строк ведем с 0:

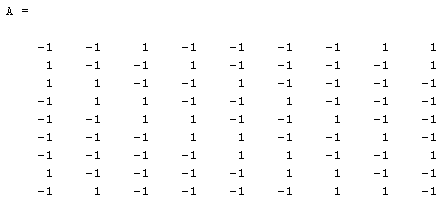
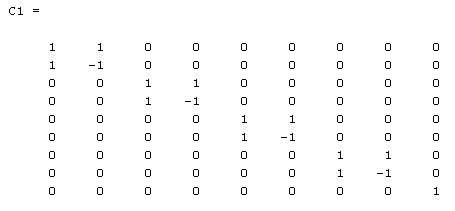
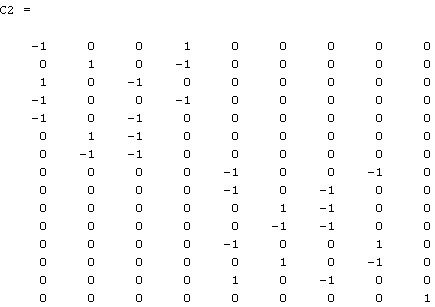
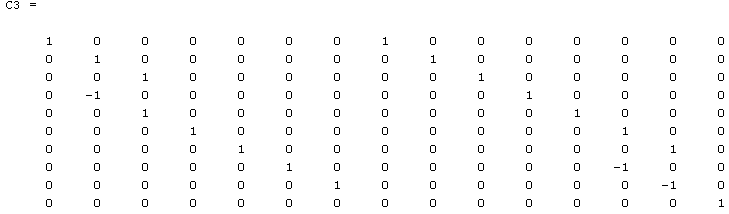
Так как в каждой строке матрицы D₃ не более 2-х ненулевых элементов, то алгоритм факторизации закончен и матрица D₃ является четвертым сомножителем факторизации.

Факторизация матрицы А этим алгоритмом будет иметь вид:

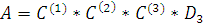
Граф вычислительного процесса.

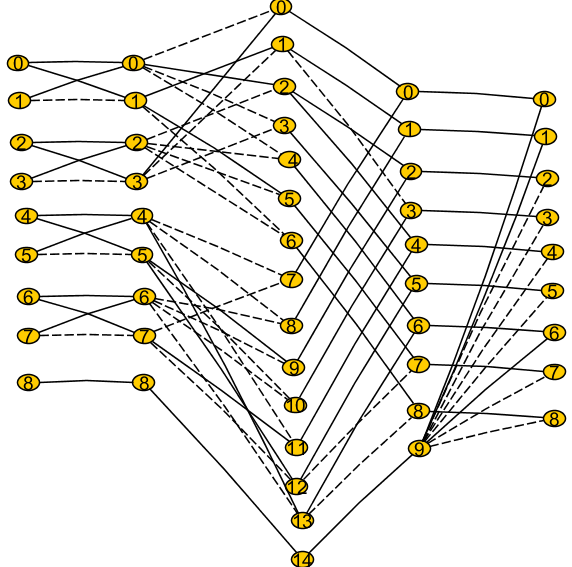
Анализ вычислительной сложности

Задание 4. Преобразования в базисе ДЭФ.

-выполнить прямое и обратное преобразование в базисе ДЭФ для длины вектора N=8.(В качестве опорного вектора используется усеченная до восьми символов третья строка матрицы циркулянта из задания №1, циклический сдвиг этой строки на пять символов используется в качестве входного сигнала);

- построить граф вычислительного процесса, осуществить оценку вычислительной сложности.

Опорный вектор S₀: -1 -1 -1 -1 1 1 -1 -1

Входной сигнал S₅: 1 -1 -1 -1 -1 -1 -1 1

Составляем матрицу вида:

W₈=

где:

W = 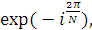где i- мнимая единица, N размер матрицы.

def(k,n) = W^kn, где k - № строки , n - № столбца

Получим:

Вычислим спектр опорного сигнала S₀. Для этого умножим матрицу W на вектор S₀:

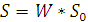
Получим :

S=

-4

-3.4142 + 1.4142i

2 - 2i

0.5858 + 1.4142i

0.5858 - 1.4142i

2+ 2i

- 3.4142 - 1.4142i

Проверим правильность нахождения спектра путем умножения полученного результата на комплексно-сопряженную матрицу V и деления на длину сигнала:

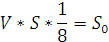
Sp =V*S*(1/8)=

-1

-0.9997

-1

-1

0.9997

-1.

-1

Вычислим спектр принятого сигнала S₅ . Для этого умножим матрицу W на S₅:

W*S5=

-4

3.4140 + 1.4140i

2 + 2i

0.5850 + 1.4140i

0.5850 - 1.4140i

2 - 2i

-3.4140 - 1.4140i

Умножим поэлементно спектр входного сигнала S₀ на комплексно сопряженный спектр принятого сигнала S₅:

M=S0,*conj(S5)=

16.0000

-9.6560 + 9.6548i

-8i

1.6560 + 1.6572i

1.6560 - 1.6572i

8i

-9.6560 - 9.6548i

Вычислим задержку сигнала, умножив результат корреляции M между спектрами на комплексно-сопряженную матрицу ДЭФ V :

conj(W)*M

Максимальная компонента равна8, ее номер 5(счет строк с 0) следовательно задержка на пять тактов.

Для построения графа вычислительного процесса факторизуем базисную матрицу ДЭФ.

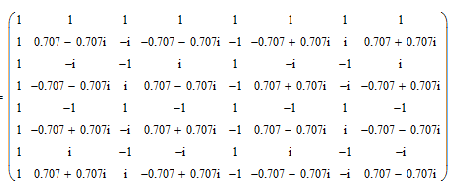
Разбиваем матрицу на 4 блока:

Сравнив соответствующие строки, получим :

Разбиваем эту матрицу на 2 блока:

Получаем по 2 ненулевых элемента в каждой строке, значит алгоритм факторизации завершен:

Граф вычислительного процесса