Взаимное положение прямой и плоскости

Прямая принадлежит плоскости – внутренняя прямая плоскости :

- имеет 2 общие точки с плоскостью (в плоскости пересекает 2 прямые);

- имеет 1 общую точку с плоскостью и параллельна некоторой прямой, принадлежащей плоскости.

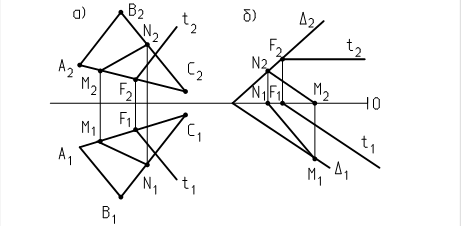Рис. 20

На рис. 20а прямая MN принадлежит плоскости (АВС), т. к. имеет с плоскостью 2 общие точки: М(MNÇАС) Þ М₂(М₂N₂Ç А₂С₂), М₁(М₁N₁Ç А₁С₁) и N(MNÇВС) Þ N₂(М₂N₂Ç B₂С₂), N₁(М₁N₁ÇB₁С₁), проекции М₁, М₂ и N_1, N₂ находятся на одних линиях связи.

Прямая t принадлежит плоскости (АВС), т. к. точка F прямой t одновременно принадлежит стороне треугольника АС Þ F₂(t ₂ Ç А₂С₂), F₁( t ₁Ç А₁С₁) и прямая t параллельна стороне АВ треугольника АВС Þ t ₂ êêА₂В₂ и t ₁ êêА₁С₁.

На рис. 20б прямая MN принадлежит плоскости D(D₁,D₂), т. к. имеет с плоскостью 2 общие точки: М(MN Ç D₂) Þ N₂(М₂N₂ Ç (D₂)₂ = D₂), N₁(М₁N₁ Ç (D₂)₁ = Х₁₂) и M(MN Ç D₁) Þ M₂(М₂N₂ Ç (D₁)₂ = X₁₂), M₁(М₁N₁ Ç (D₁)₁ = D₁), проекции М₁, М₂ и N_1, N₂ находятся на одних линиях связи.

Прямая t принадлежит плоскости D(D₁,D₂), т. к. точка F прямой t одновременно принадлежит фронтальному следу плоскости D₂ Þ F₂(t ₂ Ç (D₂)₂ = D₂), F₁(t ₁ Ç (D₂)₁ = Х₁₂) и прямая t параллельна горизонтальному следу D₁ Þ t ₂ êê(D₁)₂ = X₁₂ , t ₁ êê(D₁)₁ = D₁, проекции точки F₂ и F₁ находятся на одной линии связи к оси Х.

Внутренняя прямая плоскости относится к числу прямых, которые образуют плоскость.

Прямая не принадлежит плоскости - внешняя прямая t:

t совпадает с плоскостью, если t совпадает с некоторой

прямой d, которая принадлежит плоскости. (22)

t параллельна плоскости, если она параллельна

прямой d, которая принадлежит плоскости. (23)

t пересекает плоскость, то она пересекает

прямую d, которая принадлежит плоскости. (24)

Если учесть (22, 23, 24), то для определения взаимного положения внешней прямой и плоскости следует определить взаимное положение внешней прямой и некоторой принадлежащей плоскости прямой.

Остается выяснить, при каких исходных условиях прямая d в плоскости будет удовлетворять одновременно трем вариантам: совпадает, параллельна, пересекается с внешней прямой t.

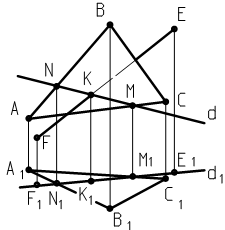На рис. 21 изображены треугольник АВС, его вторичная проек­ция на П₁ А₁В₁С₁, прямая DЕ и ее вторичная проекция F₁E₁. Для определения точки пересечения прямой FE с плоскостью АВС построена горизонтальная проекция d₁ прямой d, d₁ совпадет с гори­зонтальной проекцией F₁E₁ прямой FE. Если прямая d принадлежит тре­угольнику, то проекция прямой d₁ пересекает проекции А₁В₁ и В₁С₁ сторон треугольника в точках

Рис. 21 N₁ и M₁, которые являются проекциями точек пересечения прямой d со сторонами треугольника АВ и ВС. На линиях связи и на соответствующих сторонах найдем точки М и N, через которые пройдет прямая d . Точка К , в которой пересеклись прямые d и DE, будет точкой пересечения прямой с плоскостью треугольника. Пересекающиеся прямые d и DE образуют плоскость, которая перпендикулярна П₁, так как упомянутая плоскость содержит линии связи, перпендикулярные П₁.

Взаимное положение прямых на плоском чертеже задано системой линейных уравнений:

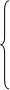
Y^d = K^d₁ ´ X^d+ C^d₁

Z^d = K^d₂ ´ X^d + C^d₂ внутренняя прямая d

Y^t = K^t₁ ´ X^t + C^t₁

Z^t = K^t₂ ´ X^t + C^t₂ внешняя прямая t

Если принять K^d₁ = K^t₁ и C^d₁ = C^t₁ (горизонтальные проекции прямых d₁ и t₁ совпадают), то взаимное положение прямых будет определено системой уравнений фронтальных проекций:

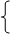Z^d = K^d₂ ´ X^d + C^d₂

Z^t = K^t₂ ´ X^t + C^t₂ .

Если K^d₂ = K^t₂ и C^d₂ = C^t₂ , то проекции прямых совпадают (внешняя прямая t лежит в плоскости).

Если K^d₂ = K^t₂ и C^d₂ ¹ C^t₂ , то фронтальные проекции прямых параллельны (внешняя прямая t параллельна плоскости).

Если K^d₂ ¹ K^t₂ , то фронтальные проекции прямых пересекаются (внешняя прямая t пересекает плоскость).

На рис. 22a заданы плоскость D(D₁,D₂) и прямая t(А₁В₁, А₂В₂). Для определения их взаимного положения в плоскости D взята прямая d(d₁,d₂), у которой горизонтальная проекция d₁ совпадает с горизонтальной проекцией А₁В₁ прямой t. Прямая d принадлежит плоскости D, следовательно, она имеет с ней общую точку N, в которой d пересекает D₂ (N₁É(D₂)₁ , N2É(D₂)₂), и прямая d параллельна горизонтальному следу плоскости D₁

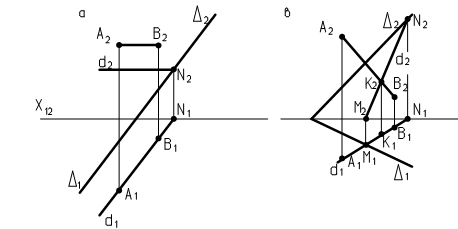
Рис. 22

(горизонтальная проекция d₁ параллельна горизонтальной проекции (D₁)₁=D₁ и фронтальная проекция d₂ параллельна фронтальной проекции (D₁)₂=Х₁₂).

Фронтальная проекция t₂(А₂В₂) внешней прямой t(А₁В₁, А₂В₂) параллельна фронтальной проекции d₂ прямой d, следовательно, на основании (23) прямая t параллельна плоскости D.

На рис. 22б заданы плоскость D(D₁,D₂) и прямая t(А₁В₁, А₂В₂). Для

определения их взаимного положения в плоскости D взята прямая d(d₁,d₂), у которой горизонтальная проекция d₁ совпадает с горизонтальной проекцией А₁В₁ прямой t. Если прямая d принадлежит плоскости D, то она в плоскости пересекает 2 прямые D₁ и D₂. Для построения фронтальной проекции определены точки пересечения М прямой d с D₁ и N прямой d с D₂. Горизонтальная проекция М₁ = d₁ Ç ((D₁)₁=D₁), фронтальная проекция М₂ = l_Х^М Ç ((D₁)₂=Х₁₂), горизонтальная проекция N₁ = d₁ Ç ((D₂)₁=Х₁₂), фронтальная проекция N₂ = l_Х^N Ç ((D₂)₂=D₂).

Фронтальная проекция t₂(А₂В₂) прямой t(А₁В₁, А₂В₂) пересекает фронтальную проекцию d₂ прямой d, следовательно,наосновании (24) прямая t пересекает плоскость Dв точке пересечения прямых t иd К(К₁,К₂).

Если принять K^d₂ = K^t₂ и C^d₂ = C^t₂ C^t₁ (фронтальные проекции прямых d₂ и t₂ совпадают), то взаимное положение прямых будет определено системой уравнений горизонтальных проекций:

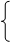Y^d = K^d₁ ´ X^d + C^d₁

Y^t = K^t₁ ´ X^t + C^t₁ .

Если K^d₁ = K^t₁ и C^d₁ = C^t₁ , то проекции прямых совпадают (внешняя прямая t лежит в плоскости).

Если K^d₁ = K^t₁ и C^d₁ ¹ C^t₁ , то горизонтальные проекции прямых параллельны (внешняя прямая t параллельна плоскости).

Если K^d₁ ¹ K^t₁ , то горизонтальные проекции прямых пересекаются (внешняя прямая t пересекает плоскость).

На рис. 23a заданы плоскость D(АВС) и прямая t(t₁, t₂). Для определения их взаимного положения в плоскости D взята прямая d(d₁,d₂), у которой фронтальная проекция d₂ совпадает с фронтальной проекцией t₂ прямой t. Если прямая d принадлежит плоскости D(АВС), то она в плоскости пересекает 2 прямые АС и ВС. Для построения горизонтальной проекции прямой определены фронтальные проекции точек пересечения М₂ = d₂ Ç А₂С₂ прямой d с АС и N₂ = d₂ Ç В₂С₂ прямой d с ВС. Горизонтальные проекции тех же точек находятся на пересечении линий связи к оси Х с соответствующими горизонтальными проекциями прямых М₁ = l_X Ç А₁С₁ и N₁ =

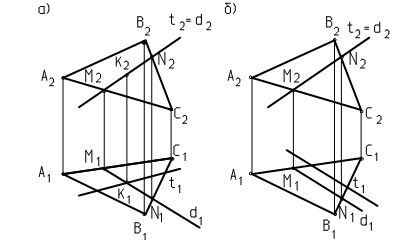Рис. 23

l_X Ç В₁С₁. Через М₁ и N₁ пройдет горизонтальная проекция d₁. Горизонтальная проекция t₁ внешней прямой t пересекает горизонтальную проекцию d₁ прямой d, следовательно,наосновании (24) прямая t пересекает плоскость Dв точке пересечения прямых t иd, точка К(К₁,К₂).

На рис. 23б горизонтальная проекция t₁ внешней прямой t параллельна горизонтальной проекции d₁ прямой d, следовательно,наосновании (23) прямая t параллельна плоскости D.

Если прямая t (рис. 24) параллельна плоскости D(ABC), то следует определить расстояние между прямой и плоскостью½t, D½, для чего достаточно изменить угол наклона плоскости, например, к П₂ до 90°. В этом случае расстояние между прямой и плоскостью будет равно расстоянию ½ D¹₂, t¹₂ ½.

Если прямая t пересекает плоскость D(ABC), то следует определить угол между прямой и плоскостью. Тогда на основании (6) необходимо построить проекцию прямой t_D на плоскость D и измерить угол между t и t_D.

На рис. 25 прямая t задана отрезком ЕМ. Для построения проекции прямой ЕМ на плоскость D(ABC) изменим в текущем положении 1 угол наклона плоскости D к П₂ до 90°. В результате на плоскость П₂ треугольник

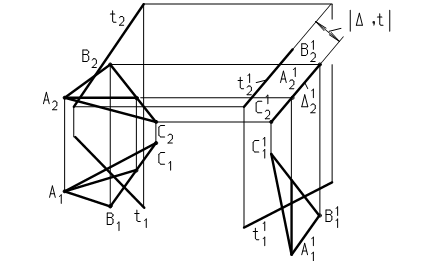Рис. 24

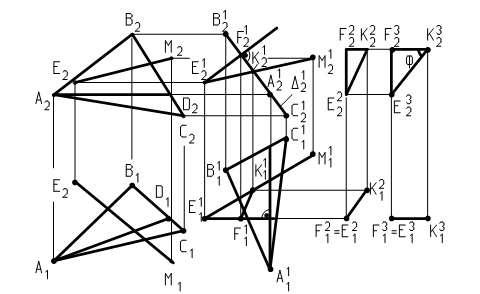
Рис. 25

спроецируется в линию – фронтальный след D¹₂. Точка К¹₂ , в которой пересеклись D¹₂ с Е¹₂М¹₂ , является фронтальной проекцией точки пересечения прямой ЕМ с плоскостью D (все точки плоскости проецируются на D¹₂ в том числе точка пересечения прямой с плоскостью). Ее горизонтальная проекция К ¹₁ расположена на пересечении линии связи с горизонтальной проекцией прямой.

Для построения проекции прямой ЕМ на плоскость D из точки Е опущен перпендикуляр EF на плоскость. На основании (20) EF перпендикулярна в плоскости двум пересекающимся прямым D¹₂ и АD. Угол b следа D¹₂ равен 0, следовательно, на основании (21) фронтальная проекция E¹₂F¹₂ перпендикулярна (D¹₂)₂ = D¹₂ , горизонтальная проекция E¹₁F¹₁ перпендикулярна горизонтальной проекции А¹₁D¹₁, т. к. угол a прямой АD равен 0 (горизонтальная и фронтальная проекции точки D в текущем положении 1 на чертеже не обозначены). Точка F(F¹₁, F¹₂) – основание перпендикуляра из точки Е на плоскость D. Прямая K¹F¹(К ¹₁ F¹₁, К¹₂F¹₂) – проекция прямой ЕМ на плоскость D.

Угол j между прямой и плоскостью будет измерен между ЕК и КF. В положении 3 угол наклона b^EKF = 0. Фронтальная проекция E³₂ К³₂ F³₂ = ÷EKF÷. Между соответствующими сторонами треугольника измерен угол j.