Задача 221.221. (завдання обласної олімпіади 1993 року) Скласти програму для гри з комп’ютером в морський бій.
Розв’язання: Одразу ж домовимось про певні обмеження, які ми накладаємо на варіант розв’язування, що приведемо ми: на полі бою розташовуються тільки однопалубні кораблі, причому вони не можуть дотикатись до інших кораблів, вводити значення місцезнаходження кораблів будемо з клавіатури. Вивід будемо здійснювати в графічному режимі для більшої наочності. Розібравшись з текстом програми ви зможете модифікувати дану програму для більш загального випадку.
Всі роздуми щодо логічної побудови програми будуть приведені в тексті програми у вигляді коментарів.
Як нам організувати робоче поле? Всім відомо, що при грі в морський бій використовують ігрове поле розміром 10 на 10 клітинок. Ми також будемо грати на полі 10 на 10, але для зручності програмування гри в пам’яті комп’ютера будемо зберігати поле 12 на 12, тобто ми з усіх сторін ігрового поля добавимо же по рядку. Зроблено це для того, щоб спростити перевірки виходу за межі ігрового поля. Отже, замість масиву mypole[1..10,1..10] ми використаємо масив mypole[0..11,0..11]. Домовимось, що при створенні математичної моделі гри будемо дотримуватись таких правил:
– якщо клітинка ігрового поля пуста і в неї не стріляли, то в ній буде міститися 0;
– якщо в даній клітинці розташовано корабель, то в ній міститься 1;
– якщо в клітинку стріляли, то в ній міститься 2.
Всі бокові клітинки, які є ніби «зайвими» і на екрані не відображаються заповними одразу двійками. Стріляти по ігровим полям будемо з комп’ютером по черзі, право першого пострілу залишимо за гравцем. Перед початком бойових дій кількості кораблів суперників прирівняємо до 10, після попадання в корабель зменшуємо відповідну кількість кораблів на 1. Бойові дії закінчується, якщо потоплено всі кораблі одного з противників.
Власне кажучи, після цього вже можна приступити до написання програми, яку ми вам і пропонуємо. Одразу зауважимо, що ми не переслідували за мету написати красиво оформлену програму, адже не це є нашою метою, нам просто потрібно показати, наскільки просто і красиво працює програма ц використанням масивів. Втім, судіть самі.
program morboj;
uses dos, crt,graph;
label mmm;
var gd,gm,i,j,l,i1,j1 : integer;
ch : char;
bul : boolean;
mypole, ibmpole : array[0..11,0..11] of byte; { для поля гри 12 на 12 }
mykor, ibmkor : integer;
k, kk : integer;
st : string;
xod : integer;
{ Очистка буферу клавiатури }
procedure och;
begin
repeat ch:=readkey until not keypressed;
end;
procedure wokrug;
var i : integer;
begin
for i:=0 to 11 do
begin
mypole[i,0]:=2; ibmpole[i,0]:=2;
mypole[i,11]:=2; ibmpole[i,11]:=2;
mypole[0,i]:=2; ibmpole[0,i]:=2;
mypole[11,i]:=2; ibmpole[11,i]:=2;
end;
end;
procedure ibmkorabel; { комп’ютер розставляє свої кораблі }
var
flag1 : boolean;
begin
kk := 10;
while kk <> 0 do
begin
flag1 := true;
i := 1 + round(random(10));
j := 1 + round(random(10));
for i1 := i-1 to i+1 do
for j1 := j-1 to j+1 do
if ibmpole[i1,j1] <> 0 then flag1 := false;
if flag1 = true then
begin
ibmpole[i,j] := 1;
dec(kk);
end;
end;
wokrug;
end;
procedure korabel; { ставимо один свій корабель }
var i1,j1 : integer;
flag1 : boolean;
begin
flag1 := true;
for i1 := i-1 to i+1 do
for j1 := j-1 to j+1 do
if getpixel(15+i1*10,15+j1*10)<>0 then flag1 := false;
if flag1 = true then
begin
Setcolor(5);
Setfillstyle(1,5);
bar(10+10*i,10+10*j,20+10*i,20+10*j);
mypole[i,j]:=1; { заповнюємо масив розташування своїх кораблів }
dec(k);
end;
end;
procedure wistrel; { наш постріл }
var i1,j1 : integer;
begin
if ibmpole[i,j] = 1 then
begin
ibmpole[i,j]:=2;
line(190+10*i,10+10*j,200+10*i,20+10*j);
line(190+10*i,20+10*j,200+10*i,10+10*j);
for i1:=i-1 to i+1 do
for j1:=j-1 to j+1 do
if ibmpole[i1,j1] = 0 then putpixel(195+10*i1,15+10*j1,1);
dec(ibmkor);
end
else
begin
putpixel(195+10*i,15+10*j,1);
xod := 0;
end
end;
procedure myxod;
begin
repeat
Setcolor(2);Rectangle(190+10*i,10+10*j,200+10*i,20+10*j);
ch := readkey;
Setcolor(1);Rectangle(190+10*i,10+10*j,200+10*i,20+10*j);
case ch of
{ вліво } #75 : dec(i);
{ вправо } #77 : inc(i);
{ вверх } #72 : dec(j);
{ вниз } #80 : inc(j);
{ пропуск } #32 : wistrel;
end; { case }
if i<1 then i := 10;
if i>10 then i := 1;
if j<1 then j := 10;
if j>10 then j := 1;
if ibmkor=0 then xod := 0;
until xod = 0;
end;
procedure ibmxod;
begin
repeat
i := round(random(10))+1;
j := round(random(10))+1;
until mypole[i,j]<>2;
putpixel(15+i*10,15+j*10,1);
if mypole[i,j]=1 then
begin
for i1:=i-1 to i+1 do
for j1:=j-1 to j+1 do
begin
mypole[i1,j1]:=2;
if (i1>0) and (i1<11) and (j1>0) and (j1<11) then
putpixel(15+i1*10,15+j1*10,1);
end;
line(10+i*10,10+j*10,20+i*10,20+j*10);
line(20+i*10,10+j*10,10+i*10,20+j*10);
dec(mykor);
end else begin mypole[i,j]:=2; xod:=1 end;
end;
{ Головна програма }
begin
gd:=CGA; gm:=0; {- 640 x 480}
mmm:
for i := 0 to 11 do
for j := 0 to 11 do
begin
mypole[i,j] := 0; { обнуляємо масив своїх кораблів }
ibmpole[i,j] := 0; { і кораблів комп’ютера }
end;
initgraph(gd,gm,'egavga.bgi');
{ малюємо поле для своїх кораблів }
setcolor(1);
mykor := 10; k := 10; { кількість моїх кораблів}
for i := 0 to 10 do line(20+10*i,20,20+10*i,120); { моє ігрове поле }
for i := 0 to 10 do line(20,20+10*i,120,20+10*i);
{ і для кораблів противника - комп’ютера }
ibmkor := 10; kk := 10; { кількість кораблів ПЕОМ}
for i := 0 to 10 do line(200+10*i,20,200+10*i,120); { ігрове поле ПЕОМ}
for i := 0 to 10 do line(200,20+10*i,300,20+10*i);
ibmkorabel;
i := 1; j := 1;
repeat
Setcolor(2);Rectangle(10+10*i,10+10*j,20+10*i,20+10*j);
ch := readkey;
Setcolor(1);Rectangle(10+10*i,10+10*j,20+10*i,20+10*j);
case ch of
{ left } #75 : dec(i);
{ right} #77 : inc(i);
{ up } #72 : dec(j);
{ down } #80 : inc(j);
#32 : korabel;
end; { case }
if i<1 then i := 10;
if i>10 then i := 1;
if j<1 then j := 10;
if j>10 then j := 1;
until k = 0;
{ А тепер можна і в бій }
xod:=1;
repeat
if (ibmkor<>0) and (mykor<>0) then if xod=1 then myxod else ibmxod;
until (ibmkor=0) or (mykor=0);
if ibmkor = 0 then outtextxy(30,150,'Ви перемогли! ')
else if mykor=0 then outtextxy(30,150,'Ви програли! ');
outtextxy(30,180,'Ще раз? (Y/N)');
ch := readkey;
st:=ch;
if (st = 'Y') or (st = 'y') then goto mmm;
closegraph;
end.
Перед розглядом наступної задачі рекомендуємо спочатку звернутись до §11.3, де описано роботу з файлами, і після ознайомлення зі згадуваними операціями повернутись до даного розділу. Ми вже з вами підійшли до того рівня, коли без операцій з файлами важко обійтись.
Задача 222.222. (ХІІІ обласна олімпіада з інформатики – м. Житомир, 1999 р.)
Шаховий кінь. У файлi CHESS.DAT задано через пропуск координати стартової А(наприклад, А5) та кiнцевої В (наприклад, С7) клiтин маршруту коня. Вивести у перший рядок файлу CHESS.SOL мiнiмальну кiлькiсть ходiв N для переходу з клiтини А на клiтину В. Наступнi N рядкiв повиннi мiстити один з можливих маршрутiв по мiнiмальному маршруту з клiтини А у клiтину В. Програма повинна мати iм'я CHESS.*
Примiтка: Клiтини шахової дошки нумеруються по горизонталi великими лiтерами латинського алфавiту: A,B,C,D,E,F,G,H, а по вертикалi цифрами 1–8.
Приклад вхiдних та вихiдних даних:
CHESS.DAT CHESS.SOL
A5 C7 4
B3
D4
B5
C7
Розв’язання: Дана задача допоможе нам познайомитись з одним цікавим методом програмування, який відноситься до методів динамічного програмування.
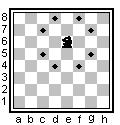 Рис. 1 Рис. 1 |
Для початку розглянемо довільне положення шахового коня на шаховій дошці. Припустимо, що кінь знаходиться у клітинці Е6. На рисунку точками відмічено клітини, у які кінь може піти при черговому ході. Таких клітин може бути від двох (у випадку, коли кінь знаходиться у кутку дошки) до восьми (як у наведеному прикладі). Ідея розв’язання полягає у відшуканні найкоротшого шляху від точки старту (Xstart, YStart) до точки фінішу (Xfine, YFine), тобто задача зводиться до відшукання найкоротшого шляху виходу з лабіринту з заданим положенням коня і точкою виходу з лабіринту (точка фінішу). Відомо багато способів відшукання такого шляху. Ми ж будемо одночасно працювати з двома шаховими дошками: одну використаємо для підрахунку кількості кроків до виходу, а іншу – для позначення номерів клітин, з яких ми потрапляємо в чергову клітину.
Обидва масиви спочатку заповнюємо нулями. Потім помічаємо клітину, у якій знаходиться кінь, як пройдену – заносимо в неї 1, причому одночасно на обох дошках.
На кожному з наступних кроків, доки не досягли клітини фінішу робимо так:
 Рис. 2. Рис. 2.
|
n переглядаємо всі клітини шахової дошки і, якщо в них міститься номер ходу, то відшукуємо всі клітини, у які може піти кінь, і заносимо в них значення номера ходу, який на 1 більше розглядуваного, а на іншій дошці вказуємо координати клітини, з якої ми в неї прийшли;
n координати клітини обраховуємо за формулою: k = X·10+Y;
n якщо досягли потрібної клітини, то встановлюємо прапорець виходу з подальшого перегляду клітин дошки, у противному випадку збільшуємо номер ходу на одиницю і повторюємо все спочатку.
Так, для наведеного в умові прикладу значення масивів для клітин обох дощок будуть мати такий вигляд, як зображено на рис. 2, 3. Стартову і кінцеву клітину маршруту виділено більш товстими лініями.
Якщо досягли потрібної клітини, то по другій дошці відшукуємо номери клітин, починаючи з кінцевої, маршруту до стартової клітини, доки значення клітини не стане рівним 1 – це означає, що ми досягли стартової клітини. На кожному кроці координати наступної клітини дошки визначаються за формулами: x = k div 10, y = k mod 10, де k – число, занесене у відповідну клітину дошки. Власне кажучи, це є використання вказівників, але без їх прямого опису. Отримані координати перетворюємо у назви клітин шахової дошки і у зворотному порядку виводимо на екран.
Описаний алгоритм розв’язання реалізовано у приведеній нижче програмі. Звертаємо увагу на необхідність акуратного оформлення перевірки можливості чергового ходу коня (процедура hod). Все інше зрозуміло з тексту програми.
program chess;
const inname = 'chess.dat';
outname = 'chess.sol';
var area, point : array[1..8,1..8] of byte;
namex : array[1..8] of char;
i, j, XStart, YStart, XFine, YFine, X, Y, step : byte;
f : text;
kod : integer;
c : char; st, st1 : string;
flag : boolean;
procedure hod(x, y, step : byte);
begin
if (x - 2 > 0) and (y - 1 > 0) and (area[x-2,y-1] = 0) then
begin
area[x-2,y-1] := step + 1;
point[x-2,y-1] := 10*x + y;
end;
if (x-2 > 0) and (y+1 < 9) and (area[x-2,y+1] = 0) then
begin
area[x-2,y+1] := step + 1;
point[x-2,y+1] := 10*x + y;
end;
if (x+2 < 9) and (y-1 > 0) and (area[x+2,y-1] = 0) then
begin
area[x+2,y-1] := step + 1;
point[x+2,y-1] := 10*x + y;
end;
if (x+2 < 9) and (y+1 < 9) and (area[x+2,y+1] = 0) then
begin
area[x+2,y+1] := step + 1;
point[x+2,y+1] := 10*x + y;
end;
if (x-1 > 0) and (y-2 > 0) and (area[x-1,y-2] = 0) then
begin
area[x-1,y-2] := step + 1;
point[x-1,y-2] := 10*x + y;
end;
if (x-1 > 0) and (y+2 < 9) and (area[x-1,y+2] = 0) then
begin
area[x-1,y+2] := step + 1;
point[x-1,y+2] := 10*x + y;
end;
if (x+1 < 9) and (y-2 > 0) and (area[x+1,y-2] = 0) then
begin
area[x+1,y-2] := step + 1;
point[x+1,y-2] := 10*x + y;
end;
if (x+1 < 9) and (y+2 < 9) and (area[x+1,y+2] = 0) then
begin
area[x+1,y+2] := step + 1;
point[x+1,y+2] := 10*x + y;
end;
end;
procedure back_and_print;
begin
assign(f, outname); rewrite(f);
st := '';
X := XFine; Y := YFine;
repeat
st1 := namex[X]; st := st + st1;
str(Y,st1); St := st + st1;
XFine := point[x,y] div 10;
YFine := point[x,y] mod 10;
x := xfine; Y := Yfine;
until point[x, y] = 1;
writeln(f, step); writeln(step);
kod := length(st) - 1;
while kod >= 1 do
begin
writeln(f,copy(st,kod,2));
writeln(copy(st,kod,2));
dec(kod,2);
end;
close(f);
end;
begin
fillchar(area, sizeof(area), 0);
fillchar(point, sizeof(point), 0);
namex[1]:='A';
for i:=2 to 8 do namex[i] := succ(namex[i-1]);
assign(f, inname); reset(f); readln(f,st); close(f);
c := st[1];
for i:=1 to 8 do if c=namex[i] then XStart := i;
c := st[2]; val(c,YStart,kod);
c := st[4];
for i:=1 to 8 do if c=namex[i] then XFine := i;
c := st[5]; val(c, YFine, kod);
X := XStart; Y: = YStart;
flag := false; step := 1;
area[xStart, yStart] := step;
point[Xstart, yStart] := 1;
while flag = false do
begin
for i := 1 to 8 do
for j := 1 to 8 do
if area[i,j] = step then hod(i, j, step);
if area[XFine,YFine] > 0
then flag := true
else inc(step);
end;
back_and_print;
end.
Вправи та завдання
223.223. Складіть програму, яка повертає квадратний масив розмірністю n на 90, 180 і 270 градусів за годинниковою стрілкою або проти годинникової стрілки, в залежності від вказівки.
224.224. У масиві розмірністю n х 12 у кожному рядку міститься заробітна плата за відповідний місяць. Складіть програму, яка:
а) підраховує сумарний заробіток кожного робітника на протязі року;
б) знаходить найменшу і найбільшу місячну заробітну плату.
225.225. Виясніть, скільки в двомірному масиві “різних чисел”. Додатковий масив не заводьте.
226.226. В заданому масиві розмірністю m на n:
а) поміняти місцями рядки з номерами k i p;
а) поміняти місцями стовпчики з номерами k i p.
227.227. В заданій квадратній матриці розміром n знайти найменший елемент, що знаходиться у відповідній заштрихованій області:
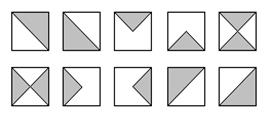
228.228. Слідом квадратної матриці називається сума елементів, розміщених на головній діагоналі. Задано квадратну матрицю порядку M і натуральне число N. Визначити сліди матриць А, А2, ..., Аn.
229.229. В заданому двомірному масиві замінити нулями елементи, що стоять в рядках або стовпчиках, де є нулі. Додаткового двомірного масиву не використовувати.
230.230.Таблиця MxN заповнена числами 0 і 1 і в таблиці контур, заповнений тільки одиницями. Всередині контуру задано клітину з нульовим значенням. Складіть програму, яка заповнює контур одиницями.
231.231. Двомірний масив заповнено невід’ємними цілими числами. Над масивом можна виконувати наступні дії: подвоєння всіх елементів в довільному стовпцю або віднімання 1 з кожного елемента довільного стовпця. Обнулити масив.
232.232. Для розв’язування систем лінійних рівнянь використовують також алгоритм Жордана, який полягає в тому, що при допомогою і–го рівняння невідоме хі вилучається не тільки з рівнянь і + 1, і + 2, ..., n, але й з рівнянь 1, 2, ..., і–1. В результаті цього прямий хід приводить до системи виду
х1 = с1
х2 = с2
...
xn = cn
і зворотний хід, який є обов’язковим в алгоритмі Гауса, виявляється не потрібним. Напишіть програму, що реалізує алгоритм Жордана.
233.233. Напишіть програму, яка виводить на екран таблицю множення у вигляді таблиці, яку іноді зображають на останній сторінці обкладинки учнівського зошита.
234.234. Для масиву розмірністю M на N, елементами якого є цілі числа у одномірний масив А вивести середнє арифметичне:
а) стовпців заданого масиву;
б) рядків заданого масиву.
235.235. Розмістити на шаховій дошці 8 ферзів так, щоб вони не загрожували один одному. Знайти всі можливі розміщення.
236.236. Розв’язати попередню задачу для випадку, коли замість ферзів у нашому розпорядженні тури.
237.237. Дано шахову дошку розміром М на N. Шахова фігура “міні–тура” може переміщуватись лише на одну клітину вліво, вправо, вверх та вниз. Двічі стати на одну й ту ж клітину фігурі заборонено. У клітинах шахової дошки розміщено деякі числа. Знайти такий шлях з клітини (1,1) в клітину (А,В), щоб сума чисел, що знаходяться у клітинах, якими пройшла фігура, дорівнювала заданому числу К, а кількість пройдених клітин – мінімальною.
238.238. Складіть програму обходу шаховим конем шахової дошки по всім клітинам, не побувавши на кожній клітині двічі.
239.239. Складіть програму, яка у прямокутному лабіринті шукає найкоротший шлях з заданої точки до виходу.
240.240. Є N населених пунктів і відома вартість проїзду між ними, якщо між ними є дорога, у противному випадку у таблиці стоїть 0. Знайти найдешевший замкнутий маршрут, що проходить через всі населені пункти.
241.241. Дано матрицю, що складається з нулів і одиниць. Знайти найбільший за площею прямокутник, що складається з одних одиниць.
242.242. Є N предметів з відомою вагою і вартістю. Знайти такий набір предметів, щоб їх сумарна вага не перевищувала вантажність автомобіля М, а вартість, була найбільшою.
Множини, записи, файли
Множини
Поняття множини є одним із основних, фундаментальних понять математики. Існує і окремий розділ математики, який так і називається – теорія множин. У звичайному шкільному курсі математики цей розділ окремо не вивчається, але знання основ теорії множин допомагають практично вирішувати велику кількість проблем, що постають у повсякденному житті.
Що ж таке множина? Не слід шукати точне визначення даного поняття, адже це можливо лише при зведенні його до чогось більш простого, а оскільки поняття множини є найпростішим, або як кажуть первинним, то і означення його давати не має смислу, так само як давати в геометрії означення поняття точки. Звичайно термін “множина” лише пояснюють на прикладах, що зробимо і ми. Сучасна людина легко розуміє поняття множини, оскільки вона звикла оперувати з множинами з дитинства. Вже на сторінках підручника математики для 1-го класу дитина бачить зображення різних множин: множину різних тварин, множину м’ячиків, множину книг, множину учнів свого класу і інших об’єктів. Людина рахує, порівнює: в одній множині більше об’єктів, в іншій – менше, і що таке множина, їй стає ясно і без всякого визначення.
У мові Паскаль множина – це довільна сукупність значень перерахованого типу. Тип множини описується наступним чином:
type < ім’я типу > = set of < тип елементів >;
Але одразу відмітимо, що кількість елементів множини у мові Паскаль не може бути більшою, ніж 256. Це пов’язано з тим, що розробники компіляторів мови Паскаль наклали саме таке обмеження на дане поняття. Проте, навіть не зважаючи на це обмеження, основні властивості множин і операції над ними можна зручно використовувати при розв’язуванні багатьох задач.
Вкажемо, що при виконанні операцій над множинами у Паскалі діють наступні операції:
n in – належність елементу множині. Звичайно використовують при перевірці умови належності множині, наприклад, нехай задано множину цифр:
cifra : set of char;
а в самій програмі на початку цю множину конкретно визначено:
cifra := [‘0’..‘9’];
Тоді перевірку належності введеного символу ch типу char на предмет належності множині цифр можна оформити як:
...
ch := readkey;
if ch in cifra then write(‘ Належить цифрам ’);
...
n + – об’єднання множин. Якщо, наприклад множина А={1,2,3,4,5}, a B={4,5,6,7}, то в результаті виконання операції С=А+В ми отримаємо С={1,2,3,4,5,6,7}.
n – – різниця множин. Якщо, наприклад множина А={1,2,3,4,5}, a B={4,5,6,7}, то в результаті виконання операції С=А–В ми отримаємо С={1,2,3}.
n * – переріз множин. Якщо, наприклад множина А={1,2,3,4,5}, a B={4,5,6,7}, то в результаті виконання операції С=А*В ми отримаємо С={4,5}.
Кого цікавить теорія множин, ми рекомендуємо звернутись до відповідної літератури, нам же цікаво як можна використати операції з множинами у програмуванні. Спочатку зовсім проста задача.
