Доверительные интервалы для математического ожидания и
Общие методические указания
При выполнении работ студенту необходимо руководствоваться следующим:
1) работа должна быть выполнена в среде Microsoft Office Excel;
2) Формулировка задания и пример выполнения приведены ниже.
Содержание первой части семестровой (контрольной) работы соответствует примерам работ (примеры 2.1; 2.2; 2.3; 2.4; 2.5; 2.6; 2.7; 2.8; 2.9). Каждое задание имеет индивидуальные исходные данные (приложение А).
Студент должен быть готов во время отчёта семестровой (контрольной) работы дать пояснения по существу выполнения работы.
Статическая обработка результатов прямых измерений
Неограниченно большая воображаемая совокупность образцов (результатов испытаний), которые могут быть выделены из исследуемого материала или полуфабриката, называют генеральной совокупностью. Ограниченную совокупность образцов (результатов испытаний), являющуюся частью генеральной совокупности, называют выборкой, а значения характеристик, вычисленные по результатам испытания выборки, называют выборочными характеристиками (статистиками) или оценками генеральных характеристик.
К оценкам предъявляются следующие требования:
а) с увеличением объема выборки п оценка 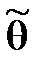 должна приближаться, т.е. сходиться по вероятности, к генеральному значению числовой характеристики. Иными словами, вероятность события, заключающегося в непревышении разницы между оценкой и генеральной характеристикой |
должна приближаться, т.е. сходиться по вероятности, к генеральному значению числовой характеристики. Иными словами, вероятность события, заключающегося в непревышении разницы между оценкой и генеральной характеристикой | 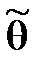 –– θ| сколь угодно малой величины, при увеличении объема выборки должна неограниченно приближаться к единице, т.е. Р (|
–– θ| сколь угодно малой величины, при увеличении объема выборки должна неограниченно приближаться к единице, т.е. Р (| 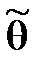 – θ| < ε) → 1. Оценку, обладающую этим свойством, называют состоятельной;
– θ| < ε) → 1. Оценку, обладающую этим свойством, называют состоятельной;
б) оценка не должна давать систематическую ошибку в сторону завышения или занижения числовой характеристики или параметра, т.е. М { 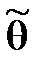 } = 0. Такую оценку называют несмещенной;
} = 0. Такую оценку называют несмещенной;
в) оценка должна быть эффективной, т.е. обладать по сравнению с другими оценками наименьшей дисперсией D{ 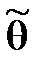 } = min.
} = min.
Используемые в математической статистике оценки не всегда удовлетворяют одновременно всем этим требованиям.
Оценка числовых характеристик и параметров
Распределения
2.1.1 Вычисление выборочных числовых характеристик при малом объеме выборки (п < 50). Выборочное среднее значение величины
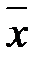 =
= 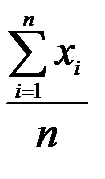 , (2.1)
, (2.1)
где xi – значение характеристики отдельных образцов; n – объем выборки.
Пример 2.1. Требуется вычислить значения выборочных среднего 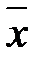 , медианы
, медианы 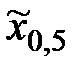 , дисперсии s2, среднего квадратического отклонения s и коэффициента вариации ν ряда значений:
, дисперсии s2, среднего квадратического отклонения s и коэффициента вариации ν ряда значений:
462, 434, 448, 477, 458, 445, 436,472, 453,468, 452, 443, 451, 456, 446, 462, 458, 445, 447, 447.
| i | xi | Предварительные расчёты: 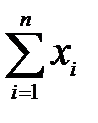 = 9060; = 9060; 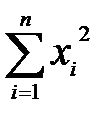 = 4106592. Выборочное среднее значение (2.1): = 4106592. Выборочное среднее значение (2.1): 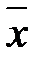 = = 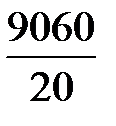 = 453. Выборочная медиана (2.3): = 453. Выборочная медиана (2.3): 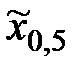 = = 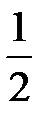 (451 + 452) = 451,5. Выборочная дисперсия (2.5): s2 = (451 + 452) = 451,5. Выборочная дисперсия (2.5): s2 = 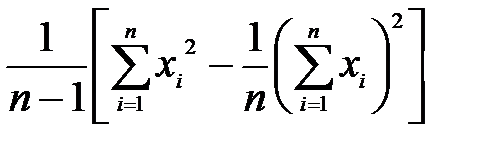 = = 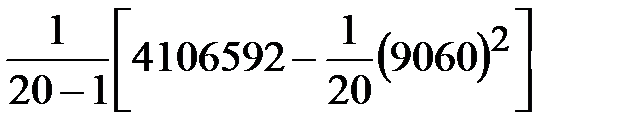 = = 126,9 Смещённая оценка среднего квадратического отклонения (2.6): s = = = 126,9 Смещённая оценка среднего квадратического отклонения (2.6): s = 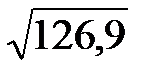 = 11,26. Несмещённая оценка среднего квадратического отклонения (2.8) и таблица 2.1: s1 = 1,013 · 11,26 = 11,41. Выборочный коэффициент вариации (2.7): ν = = 11,26. Несмещённая оценка среднего квадратического отклонения (2.8) и таблица 2.1: s1 = 1,013 · 11,26 = 11,41. Выборочный коэффициент вариации (2.7): ν = 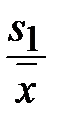 = = 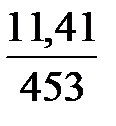 = 0,0252. = 0,0252. |
Выборочная медиана при нечётном объеме выборки n = 2m – 1 равна среднему члену вариационного ряда:
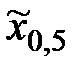 = xm, (2.2)
= xm, (2.2)
при чётном объеме n = 2m
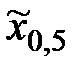 =
= 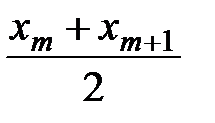 . (2.3)
. (2.3)
Выборочная дисперсия
s2 = 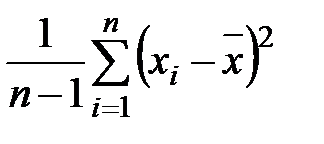 , (2.4)
, (2.4)
или
s2 = 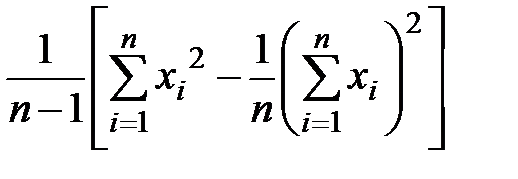 . (2.5)
. (2.5)
Выборочное среднее квадратическое отклонение и выборочный коэффициент вариации
s = 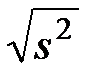 , (2.6)
, (2.6)
ν = 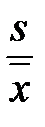 . (2.7)
. (2.7)
Вычисление выборочных моментов третьего и четвёртого порядков при объёме п < 50 нецелесообразно в связи с их большими вероятными отклонениями от генеральных моментов.
Для нормально распределённой генеральной совокупности оценки 4, 7, 8 являются состоятельными, эффективными и несмещёнными. Оценка 9 является эффективной, состоятельной, но смещённой. Несмещённая оценка среднего квадратического отклонения
s1 = k s, (2.8)
где k – поправочный коэффициент (таблица 2.1).
Таблица 2.1 – Значения поправочного коэффициента k
| n | k | n | k | n | k | n | k | n | k |
| 1,253 1,128 1,085 1,064 1,051 1,042 | 1,036 1,032 1,028 1,025 1,023 1,021 | 1,019 1,018 1,017 1,016 1,015 1,014 | 1,013 1,010 1,008 1,007 1,006 1,006 | 1,005 1,004 1,004 |
2.1.2 Вычисление выборочных числовых характеристик при большом объеме выборки (п > 50). Необходимо предварительно систематизировать исходные данные, что при п < 50 является лишь желательным. Систематизация заключается в представлении результатов испытаний в виде вариационного ряда
x1 ≤ x2 ≤ … ≤ xi ≤ … ≤ xn
Производят группировку результатов испытаний, для чего размах варьирования рассматриваемой характеристики
R = xmax – xmin (2.9)
Разбивают на 7 … 20 равных интервалов и подсчитывают частоту (число наблюдений), заключённых в каждом интервале.
Количество интервалов: 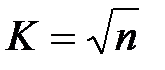 .
.
Выборочное средне значение рассматриваемой характеристики
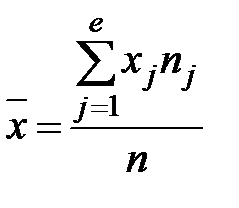 , (2.10)
, (2.10)
где xj – значение характеристики в середине j-го интервала; nj – частота (число наблюдений), заключённых в j-м интервале; е – число интервалов.
Выборочная дисперсия
s2 = 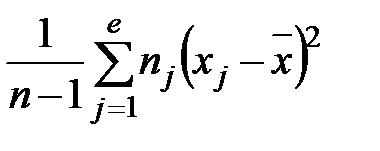 , (2.11)
, (2.11)
или
s2 = 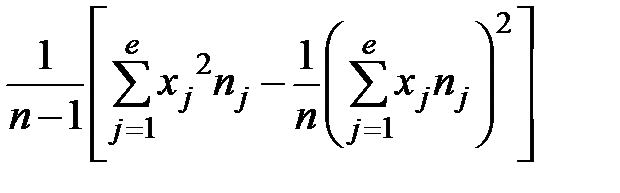 (2.12)
(2.12)
Группировка данных приводит к некоторой неточности расчёта 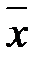 и s2 по формулам 2.10 – 2.12 по сравнению с формулами 2.1, 2.4 и 2.5, однако при этом погрешностью модно пренебречь, если е ≤ 7.
и s2 по формулам 2.10 – 2.12 по сравнению с формулами 2.1, 2.4 и 2.5, однако при этом погрешностью модно пренебречь, если е ≤ 7.
Выборочное среднее и выборочный коэффициент вариации определяют по формулам 2.6 и 2.7 без поправки на смещение.
Для нахождения показателей асимметрии и эксцесса выборочного распределения предварительно находят выборочные начальные моменты распределения
h1 = 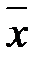 =
= 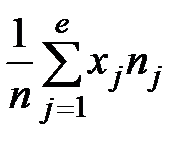 ; h2 =
; h2 = 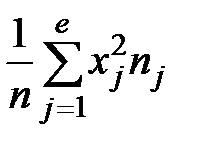 ;
;
h3 = 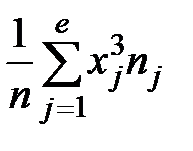 ; h4 =
; h4 = 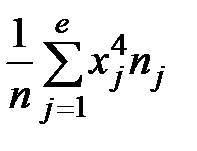 . (2.13)
. (2.13)
и выборочные центральные моменты
m3 = h3 – 3 h2 h1 + 2 h13;
m4 = h4 – 4 h3 h1 + 6 h2 h12 – 3 h14. (2.14)
Выборочные показатели асимметрии и эксцесса
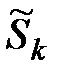 =
= 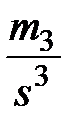 ; (2.15)
; (2.15)
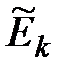 =
= 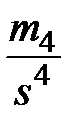 – 3. (2.16)
– 3. (2.16)
Пример 2.2. Вычислить значения статистик, указанных в примере 2.1, и выборочные значения показателей асимметрии и эксцесса для случайной величины x = lgN. Ряд значений N:
6559942; 7326558; 7442177; 7901326; 8037112; 8145167; 8296597; 8509421; 9005338; 12089268; 14729907; 18209583; 18945235; 28747495; 2404916; 2414905; 2420472; 2464904; 2492872; 2556230; 2562123; 2566847; 2639976; 2708944; 2717691; 2897344; 2904023; 2914741; 2953929; 736037,6; 824897,5; 1050993; 1092949; 1103062; 1107899; 1160112; 1201988; 1208092; 1277027; 1282921; 1313107; 1314014; 1329842; 1447105; 1474009; 1494858; 1513910; 1545966; 1567112; 1611017; 1621810; 1697071; 1823056; 2048802; 2142891; 2337760; 2369191; 2960056; 3049299; 3144126; 3150649; 3295338; 3312074; 3322003; 3329661; 3492207; 3518844; 3612435; 3633289; 3636637; 3676207; 3677054; 3795771; 3822082; 3904811; 3941849; 4070052; 4437108; 4440174; 4719544; 4719544; 4764310; 4893279; 4915866; 5011872; 5112108; 5166542; 5221557; 5244451; 5339493; 5339493; 5485295; 5536050; 5672833; 6038096; 6273357; 6273357; 6292164; 6365023; 6519285
Производим логарифмирование и формируем вариационный ряд.
Таблица 2.2
| i | xi = lgNi | i | xi = lgNi | i | xi = lgNi | i | xi = lgNi | i | xi = lgNi | i | xi = lgNi |
| 5,8669 | 6,1801 | 6,4086 | 6,5431 | 6,6896 | 6,8142 | ||||||
| 5,9164 | 6,1892 | 6,4094 | 6,5464 | 6,6916 | 6,8169 | ||||||
| 6,0216 | 6,1951 | 6,4216 | 6,5578 | 6,7 | 6,8649 | ||||||
| 6,0386 | 6,2071 | 6,4328 | 6,5603 | 6,7086 | 6,8717 | ||||||
| 6,0426 | 6,21 | 6,4342 | 6,5607 | 6,7132 | 6,8977 | ||||||
| 6,0445 | 6,2297 | 6,462 | 6,5654 | 6,7178 | 6,9051 | ||||||
| 6,0645 | 6,2608 | 6,463 | 6,5655 | 6,7197 | 6,9109 | ||||||
| 6,0799 | 6,3115 | 6,4646 | 6,5793 | 6,7275 | 6,9189 | ||||||
| 6,0821 | 6,331 | 6,4704 | 6,5823 | 6,7275 | 6,9299 | ||||||
| 6,1062 | 6,3688 | 6,4713 | 6,5916 | 6,7392 | 6,9545 | ||||||
| 6,1082 | 6,3746 | 6,4842 | 6,5957 | 6,7432 | 7,0824 | ||||||
| 6,1183 | 6,3811 | 6,4975 | 6,6096 | 6,7538 | 7,1682 | ||||||
| 6,1186 | 6,3829 | 6,4984 | 6,6471 | 6,7809 | 7,2603 | ||||||
| 6,1238 | 6,3839 | 6,5179 | 6,6474 | 6,7975 | 7,2775 | ||||||
| 6,1605 | 6,3918 | 6,5201 | 6,6739 | 6,7975 | 7,4586 | ||||||
| 6,1685 | 6,3967 | 6,5214 | 6,6739 | 6,7988 | |||||||
| 6,1746 | 6,4076 | 6,5224 | 6,678 | 6,8038 |
Определяем размах варьирования логарифма:
R = 7,4586 – 5,8669 = 1,5917.
Размах разбиваем на равные интервалы.
Δx ≈ 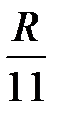 =
= 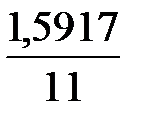 = 0,1447
= 0,1447
За длину интервала принимаем Δx = 0,15
Таблица 2.3
| e | Границы интервала | Середина интервала xj | Число наблюдений nj |
| 5,825 … 5,975 | 5,90 | ||
| 5,975 … 6,125 | 6,05 | ||
| 6,125 … 6,275 | 6,20 | ||
| 6,275 … 6,425 | 6,35 | ||
| 6,425 … 6,575 | 6,50 | ||
| 6,575 … 6,725 | 6,65 | ||
| 6,725 … 6,875 | 6,80 | ||
| 6,875 … 7,025 | 6,95 | ||
| 7,025 … 7,175 | 7,10 | ||
| 7,175 … 7,325 | 7,25 | ||
| 7,325 … 7,475 | 7,40 |
Предварительные расчёты:
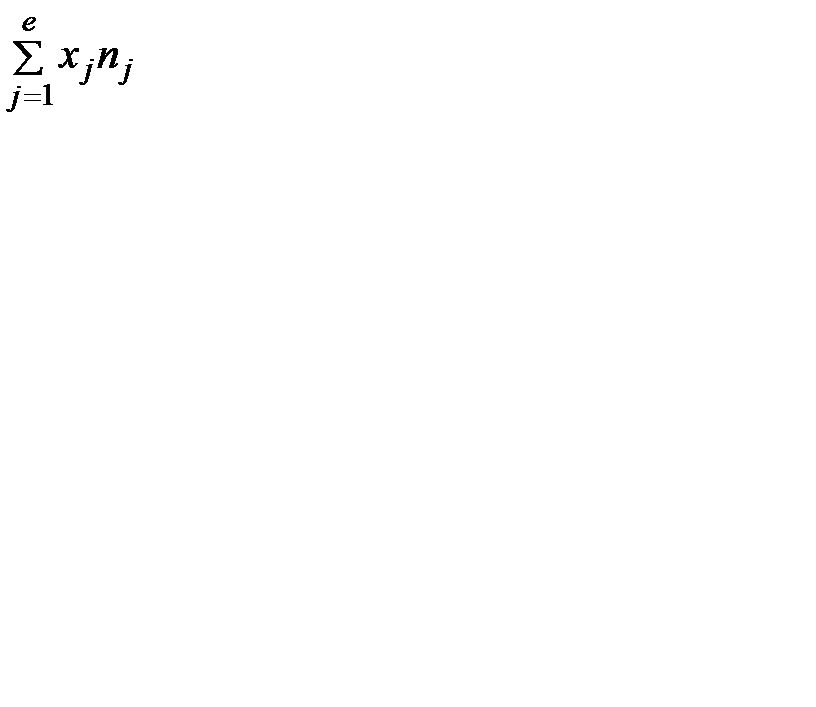 = 651,5;
= 651,5; 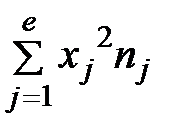 = 4254,355;
= 4254,355;
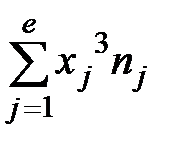 = 27845,945;
= 27845,945; 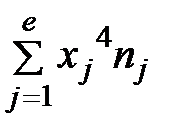 = 182684,833.
= 182684,833.
Выборочное среднее значение (2.10):
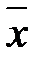 =
= 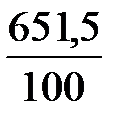 = 6,515.
= 6,515.
Выборочная медиана (2.3):
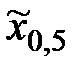 =
= 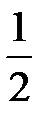 (6,5214 + 6,5224) = 6,5219.
(6,5214 + 6,5224) = 6,5219.
Выборочная дисперсия (2.12):
s2 = 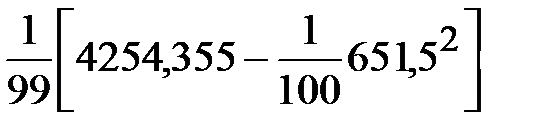 = 0,09932.
= 0,09932.
Выборочное среднее и выборочный коэффициент вариации (2.6) и (2.7):
s = 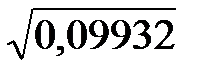 = 0,315; ν =
= 0,315; ν = 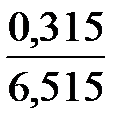 = 0,0484.
= 0,0484.
Для вычисления выборочных показателей ассиметрии и эксцесса по формулам (2.13) определяем оценки начальных моментов первых четырёх порядков:
h1 = 6,515; h2 = 42,5435;
h3 = 278,45945; h4 = 1826,848332
и по формулам (2.14) – оценки центральных моментов третьего и четвёртого порядка
m3 = 0,00705;
m4 = 0,026974.
Выборочные показатели ассиметрии и эксцесса
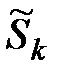 =
= 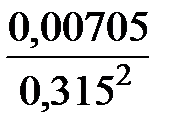 = 0,226;
= 0,226; 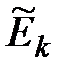 =
= 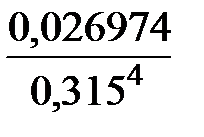 –3 = –0,260.
–3 = –0,260.
2.1.3 Оценка среднего квадратического отклонения по результатам испытаний нескольких выборок.Если из нормально распределённой генеральной совокупности испытано m выборок объёмом n каждая, то оценкой генерального среднего квадратического отклонения может служить статистика
s = 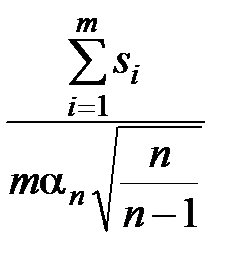 , (2.17)
, (2.17)
где si – выборочное среднее квадратического отклонение случайной величины, определяемое по формуле (2.6); αn – коэффициент, зависящий от объёма выборки.
Другая оценка среднего квадратического отклонения по совокупности малых выборок с учётом размахов варьирования в каждой выборке Ri, применима при постоянном объёме выборки, взятой из нормально распределённой генеральной совокупности.
s = 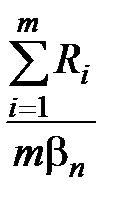 , (2.18)
, (2.18)
Таблица 2.4 – Значения коэффициентов для оценки среднего квадратического отклонения
| n | αn | βn | γn | n | αn | βn | γn |
| 0,5642 0,7236 0,7979 0,8407 0,8686 0,8882 0,9027 0,9139 0,9227 0,9300 | 1,128 1,693 2,059 2,326 2,534 2,704 2,847 2,970 3,078 3,173 | 0,756 0,525 0,427 0,371 0,335 0,308 0,288 0,272 0,259 0,248 | 0,9359 0,9410 0,9453 0,9490 0,9523 0,9551 0,9576 0,9599 0,9619 | 3,258 3,336 3,407 3,472 3,532 3,588 3,640 3,689 3,735 | 0,239 0,231 0,224 0,217 0,212 0,207 0,203 0,199 0,195 |
2.1.4Для сокращения стоимости и времени часть образцов снимают м испытаний при достижении ими базового значения. В этих условиях образуется цензурированная справа выборка, содержащая n элементов, m из которых разрушались до требуемого уровня, а n – m сняты с испытания, у них значения x > xб, т. е. больше базового значения. Вариационный ряд в этом случае имеет вид
x1 ≤ x2 ≤ … ≤ xi ≤ … ≤ xm, m < n. (2.19)
Определяют значение степени усечения выборки
W = 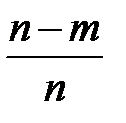 . (2.20)
. (2.20)
Вычисляют значение
y = 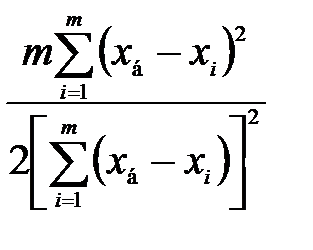 , (2.21)
, (2.21)
и по таблице в соответствии с вычисленными значениями W и y находят величину u. Представляющую собой оценку для нормированной точки усечения.
Таблица 2.5 – Значение u для цензурированной выборки
| y | W = 0,05 | 0,10 | 0,15 | 0,20 | 0,25 | 0,30 | 0,35 | 0,40 | 0,45 | 0,50 |
| 0,500 0,505 0,510 0,515 0,520 0,525 0,530 0,535 0,540 0,545 0,550 0,555 0,560 0,565 0,570 0,575 0,580 0,585 0,590 0,595 0,600 0,610 0,620 0,630 0,640 0,650 0,660 0,670 0,680 0,690 0,700 0,710 0,720 0,730 0,740 0,750 0,760 0,770 0,780 0,790 0,800 0,850 0,900 0,950 1,000 1,150 1,100 1,150 1,200 1,250 1,300 1,350 1,400 1,450 1,500 | -2,922 -2,786 -2,667 -2,562 -2,468 -2,384 -2,308 -2,239 -2,175 -2,117 -2,063 -2,013 -1,966 -1,923 -1,882 -1,844 -1,773 -1,710 -1,654 -1,602 -1,555 -1,512 1,472 -1,435 -1,401 1,369 -1,339 -1,311 -1,285 -1,260 -1,236 -1,214 -1,193 -1,173 -1,154 -1,135 -1,055 -0,989 -0,934 -0,887 -0,847 -0,811 -0,779 -0,751 -0,725 -0,702 -0,680 -0,661 -0,643 -0,626 | -2,680 -2,555 -2,445 -2,349 -2,263 -2,185 -2,115 -2,051 -1,992 -1,939 -1,889 -1,843 -1,800 -1,760 -1,722 -1,686 -1,653 -1,621 -1,591 -1,563 -1,536 -1,486 -1,441 -1,399 -1,360 -1,325 -1,292 -1,261 -1,233 -1,206 -1,180 -1,156 -1,134 -1,113 -1,092 -1,073 -1,055 -1,038 -1,021 -1,005 -0,990 -0,922 -0,866 -0,819 -0,778 -0,742 -0,711 -0,682 -0,657 -0,634 -0,613 -0,594 -0,576 -0,560 -0,545 | -1,985 -1,921 -1,862 -1,809 -1,759 -1,714 -1,671 -1,632 -1,595 -1,560 -1,528 -1,497 -1,468 -1,441 -1,415 -1,390 -1,366 -1,344 -1,322 -1,302 -1,282 -1,245 -1,211 -1,180 -1,150 -1,123 -1,097 -1,073 -1,050 -1,029 -1,009 -0,989 -0,971 -0,954 -0,937 -0,921 -0,906 -0,892 -0,878 -0,865 -0,852 -0,795 -0,747 -0,706 -0,671 -0,639 -0,611 -0,586 -0,564 -0,544 -0,525 -0,507 -0,491 -0,477 -0,463 | -1,537 -1,499 -1,463 -1,429 -1,398 -1,369 -1,340 -1,314 -1,289 -1,265 -1,242 -1,221 -1,200 -1,180 -1,162 -1,144 -1,127 -1,110 -1,094 -1,079 -1,064 -1,036 -1,010 -0,986 -0,963 -0,941 -0,921 -0,902 -0,884 -0,866 -0,850 -0,834 -0,819 -0,805 -0,792 -0,779 -0,766 -0,754 -0,742 -0,731 -0,721 -0,673 -0,631 -0,596 -0,565 -0,538 -0,513 -0,491 -0,471 -0,453 -0,436 -0,421 -0,406 -0,393 -0,381 | -1,207 -1,182 -1,158 -1,135 -1,114 -1,093 -1,074 -1,055 -1,037 -1,020 -1,004 -0,988 -0,973 -0,959 -0,945 -0,932 -0,919 -0,906 -0,894 -0,882 -0,871 -0,850 -0,829 -0,810 -0,792 -0,775 -0,759 -0,744 -0,729 -0,715 -0,702 -0,702 -0,689 -0,677 -0,665 -0,654 -0,643 -0,632 -0,613 -0,603 -0,594 -0,553 -0,518 -0,488 -0,461 -0,437 -0,415 -0,396 -0,378 -0,362 -0,347 -0,333 -0,320 -0,308 -0,297 | -0,943 -0,925 -0,909 -0,893 -0,877 -0,863 -0,849 -0,835 -0,822 -0,809 -0,797 -0,786 -0,774 -0,763 -0,753 -0,743 -0,733 -0,723 -0,714 -0,705 -0,696 -0,679 -0,663 -0,648 -0,634 -0,620 -0,607 -0,595 -0,583 -0,572 -0,561 -0,561 -0,550 -0,540 -0,530 -0,521 -0,512 -0,503 -0,487 -0,479 -0,471 -0,437 -0,407 -0,380 -0,357 -0,336 -0,317 -0,300 -0,284 -0,270 -0,257 -0,244 -0,233 -0,222 -0,212 | -0,720 -0,707 -0,695 -0,683 -0,672 -0,661 -0,651 -0,641 -0,631 -0,621 -0,612 -0,603 -0,595 -0,587 -0,579 -0,571 -0,563 -0,555 -0,548 -0,541 -0,534 -0,521 -0,508 -0,496 -0,485 -0,474 -0,463 -0,453 -0,444 -0,425 -0,417 -0,408 -0,400 -0,393 -0,385 -0,378 -0,371 -0,364 -0,364 -0,357 -0,351 -0,322 -0,296 -0,273 -0,253 -0,235 -0,219 -0,203 -0,189 -0,177 -0,165 -0,154 -0,144 -0,134 -0,125 | -0,523 -0,514 -0,505 -0,496 -0,488 -0,480 -0,472 -0,464 -0,457 -0,450 -0,443 -0,436 -0,429 -0,423 -0,416 -0,410 -0,404 -0,399 -0,393 -0,387 -0,382 -0,371 -0,361 -0,352 -0,343 -0,334 -0,325 -0,317 -0,309 -0,301 -0,294 -0,287 -0,280 -0,273 -0,267 -0,261 -0,255 -0,249 -0,243 -0,238 -0,232 -0,207 -0,186 -0,166 -0,149 -0,133 -0,119 -0,105 -0,093 -0,082 -0,072 -0,062 -0,053 -0,044 -0,036 | -0,345 -0,338 -0,331 -0,325 -0,318 -0,312 -0,306 -0,300 -0,295 -0,289 -0,284 -0,278 -0,273 -0,268 -0,263 -0,258 -0,254 -0,249 -0,245 -0,240 -0,236 -0,228 -0,220 -0,212 -0,204 -0,197 -0,190 -0,184 -0,177 -0,171 -0,166 -0,160 -0,154 -0,148 -0,143 -0,138 -0,133 -0,128 -0,123 -0,118 -0,114 -0,093 -0,074 -0,058 -0,043 -0,029 -0,017 -0,005 0,006 0,016 0,025 0,033 0,041 0,049 0,056 | -0,178 -0,173 -0,168 -0,163 -0,158 -0,154 -0,149 -0,144 -0,140 -0,136 -0,132 -0,128 -0,124 -0,120 -0,116 -0,112 -0,108 -0,105 -0,101 -0,098 -0,094 -0,087 -0,081 -0,075 -0,069 -0,063 -0,058 -0,052 -0,047 -0,042 -0,037 -0,032 -0,027 -0,023 -0,019 -0,014 -0,010 -0,006 -0,002 0,002 0,006 0,023 0,039 0,053 0,066 0,077 0,088 0,098 0,107 0,116 0,124 0,131 0,138 0,145 0,151 |
Вычисляют оценку математического ожидания
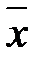 =
= 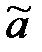 = xб + us. (2.22)
= xб + us. (2.22)
Определяют оценку среднего квадратического отклонения
s = 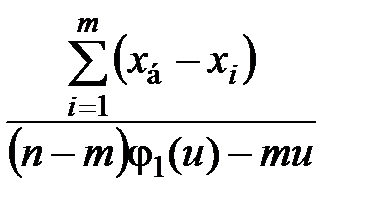 , (2.23)
, (2.23)
где φ1(u) определяют по найденному значению u.
Пример 2.3. По данным примера 2.2 произвести оценку математического ожидания и среднего квадратического отклонения при условии, что испытания прекращали при достижении базы Nб = 5·106 циклов, т.е. xб = = lg Nб = 6,6990.
По таблице 2.2 находим m = 70 и по формуле (2.20) вычисляем:
W = 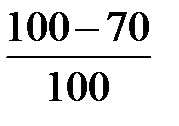 = 0,30.
= 0,30.
По формуле (2.21)
y = 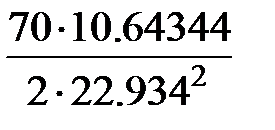 = 0,7083.
= 0,7083.
По таблице 2.5 для W = 030 и y = 0,7083 путём линейной интерполяции находи u = –0,552.
По таблице 2.6 находим
φ1(–0,552) = 1,1795
По формуле (2.23) производим оценку среднего квадратического отклонения s = 0,301
По формуле (2.22) производим оценку математического ожидания
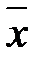 =
= 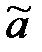 = 6,6990 – 0,552 · 0,301 = 6,533.
= 6,6990 – 0,552 · 0,301 = 6,533.
Таблица 2.6 – Значение функции для цензурированной выборки
| и | φ1(u) | φ2(u) | φ3(u) | и | φ1(u) | φ2(u) | φ3(u) |
| -3,0 | 3,2831 | 1,000 | 0,5012 | -0,4 | 1,0688 | 1,189 | 0,8911 |
| -2,9 | 3,1903 | 1,000 | 0,5016 | -о,з | 0,99817 | 1,243 | 0,9592 |
| -2,8 | 3,0979 | 1,000 | 0,5022 | -0,2 | 0,92942 | 1,312 | 1,039 |
| -2,7 | 3,0058 | 1,000 | 0,5030 | -0,1 | 0,86262 | 1,401 | 1,132 |
| -2,6 | 3,9141 | 1,000 | 0,5040 | 0,0 | 0,79788 | 1,517 | 1,241 |
| -2,5 | 2,8227 | 1,001 | 0,5052 | 0,1 | 0,73533 | 1,667 | 1,370 |
| -2,4 | 2,7318 | 1,001 | 0,5069 | 0,2 | 0,67507 | 1,863 | 1,523 |
| -2,3 | 2,6414 | 1,001 | 0,5090 | 0,3 | 0,61722 | 2,118 | 1,704 |
| -2,2 | 2,5515 | 1,001 | 0,5117 | 0,4 | 0,56188 | 2,453 | 1,919 |
| -2,1 | 2,4621 | 1,002 | 0,5149 | 0,5 | 0,50916 | 2,893 | 2,178 |
| -2,0 | 2,3732 | 1,003 | 0,5190 | 0,6 | 0,45915 | 3,473 | 2,488 |
| -1,9 | 2,2849 | 1,004 | 0,5239 | 0,7 | 0,41192 | 4,241 | 2,863 |
| -1,8 | 2,1973 | 1,005 | 0,5299 | 0,8 | 0,36756 | 5,261 | 3,319 |
| -1,7 | 2,1103 | 1,006 | 0,5371 | 0,9 | 0,32611 | 6,623 | 3,876 |
| -1,6 | 2,0241 | 1,009 | 0,5458 | 1,0 | 0,28760 | 8,448 | 4,561 |
| -1,5 | 1,9387 | 1,011 | 0,5562 | 1,1 | 0,25205 | 10,90 | 5,408 |
| -1,4 | 1,8541 | 1,015 | 0,5685 | 1,2 | 0,21944 | 14,22 | 6,462 |
| -1,3 | 1,7704 | 1,019 | 0,5830 | 1,3 | 0,18974 | 18,73 | 7,780 |
| -1,2 | 1,6876 | 1,025 | 0,6000 | 1,4 | 0,16288 | 24,89 | 9,442 |
| -1,1 | 1,6058 | 1,032 | 0,6200 | 1,5 | 0,13879 | 33,34 | 11,55 |
| -1,0 | 1,5251 | 1,042 | 0,6434 | 1,6 | 0,11735 | 44,99 | 14,24 |
| -0,9 | 1,4456 | 1,054 | 0,6707 | 1,7 | 0,098436 | 61,13 | 17,71 |
| -0,8 | 1,3674 | 1,069 | 0,7025 | 1,8 | 0,081893 | 83,64 | 22,19 |
| -0,7 | 1,2905 | 1,089 | 0,7395 | 1,9 | 0,067556 | 115,2 | 28,05 |
| -0,6 | 1,2150 | 1,114 | 0,7826 | 2,0 | 0,055248 | 159,7 | 35,74 |
| -0,5 | 1,1411 | 1,147 | 0,8327 |
Доверительные интервалы для математического ожидания и
Дисперсии
Представление об уровне точности и надёжности оценок дают так называемые доверительные интервалы, смысл которых состоит в том, что для любой малой вероятности α можно указать такое значение ε= | 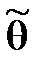 – θ|, при котором
– θ|, при котором
Р ( 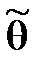 – ε < θ <
– ε < θ < 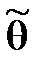 + ε) = 1 – α (2.24)
+ ε) = 1 – α (2.24)
Если многократно повторять выборки и каждый раз находить доверительные интервалы, то в (1 – α) 100 % случаев доверительные интервалы накроют истинное значение интересующего нас параметра. Соответствующую вероятность Р = 1 – α называют доверительной вероятностью или статистической надёжностью.
Уровни доверительной вероятности обычно принимают равными 0,9 или 0,95, реже 0,99.
Доверительные границы определяются интервалом
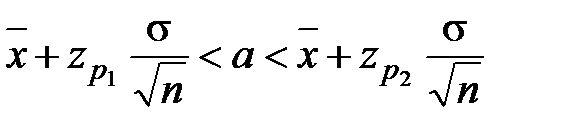 (2.25)
(2.25)
Обычно принимают симметричные границы доверительных интервалов, т.е. Р1 = α/2 и Р2 = 1 – Р1 = 1 – α/2.
Таблица 2.7 – Значения квантилей нормированного нормального распределения
| Р | zp | Р | zp | Р | zp | Р | zp |
| 0,0001 0,001 0,005 0,01 0,025 | –∞ –3,719 –3,090 –2,576 –2,326 –1,960 | 0,05 0,1 0,2 0,3 0,4 0,5 | –1,645 –1,282 –0,842 –0,524 –0,253 | 0,6 0,7 0,8 0,9 0,95 0,975 | 0,253 0,524 0,842 1,282 1,645 1,960 | 0,99 0,995 0,999 0,9999 | 2,326 2,576 3,090 3,719 ∞ |
Если значение генеральной дисперсии исходного распределения неизвестно, то используют выборочную дисперсию.
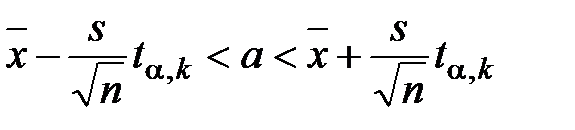 , (2.26)
, (2.26)
где tα, k – значение квантили статистики t = 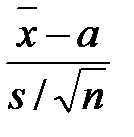 уровня Р = 1 – α/2 для числа степеней свободы k = n – 1.
уровня Р = 1 – α/2 для числа степеней свободы k = n – 1.
Таблица 2.8 – Значения α-пределов tα, k распределения Стьюдента в зависимости от числа свободы k
| k | α | |||||
| 0,1 | 0,05 | 0,025 | 0,01 | 0,005 | 0,001 | |
| ∞ | 6,314 2,920 2,353 2,132 2,015 1,943 1,895 1,860 1,833 1,812 1,782 1,761 1,746 1,734 1,725 1,717 1,711 1,706 1,701 1,697 1,645 | 12,706 4,303 3,182 2,776 2,571 2,447 2,365 2,306 2,262 2,228 2,179 2,145 2,120 2,101 2,086 2,074 2,064 2,056 2,048 2,042 1,960 | 25,452 6,205 4,177 3,495 3,163 2,969 2,841 2,752 2,685 2,634 2,560 2,510 2,473 2,445 2,423 2,405 2,391 2,379 2,369 2,360 2,241 | 60,657 9,925 5,841 4,604 4,032 3,707 3,499 3,355 3,250 3,169 3,055 2,977 2,921 2,818 2,845 2,819 2,797 2,779 2,763 2,750 2,576 | 127,3 14,089 7,453 5,597 4,773 4,317 4,029 3,833 3,690 3,581 3,428 3,326 3,252 3,193 3,153 3,119 3,092 3,067 3,047 3,030 2,807 | 636,6 31,600 12,922 8,610 6,869 5,959 5,408 5,041 4,781 4,587 4,318 4,140 4,015 3,922 3,849 3,792 3,745 3,704 3,674 3,646 3,291 |
Пример 2.4. По результатам примера 2.1 определить 90 %-ные доверительные интервалы для генерального среднего значения, если 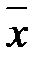 = 453; s = 11,26.
= 453; s = 11,26.
По таблице 2.6 для k = 20 – 1 = 19 и α = 0,1 находим t0,1 = 1,73.
На основании формулы (2.26)
453 – 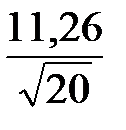 1,73 < a < 453 +
1,73 < a < 453 + 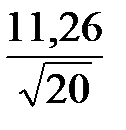 1,73;
1,73;
449 < a < 457.
В случае цензурированной выборки доверительный интервал для доверительной вероятности Р = 1 – α приближённо определяют из выражения
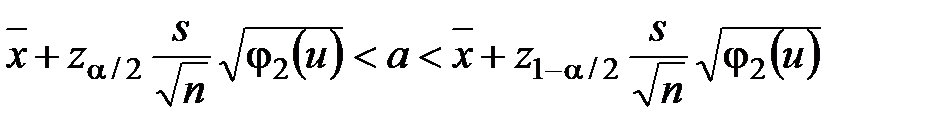 (2.27)
(2.27)
Пример 2.5. По результатам таблицы 2.2 определить 90 %-ные доверительные интервалы для генерального среднего значения, если 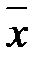 = 6,533; s = 0,301; u = –0,552 (см. пример 2.3).
= 6,533; s = 0,301; u = –0,552 (см. пример 2.3).
Для α = 0,1 по таблице 2.7 находим
z0,05 = –1,64;
z0,95 = 1,64.
По найденному в примере 2.3 u = –0,552 по таблице 2.6
φ2(0,552) = 1,130.
На основании (2.27)
6,533 – 1,64 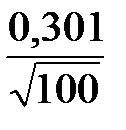
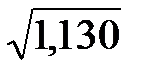 < a < 6,533 + 1,64
< a < 6,533 + 1,64 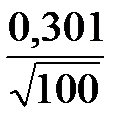
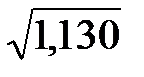
6,4805 < a < 6,5855
Доверительный интервал для генеральной дисперсии σ2 с доверительной вероятностью Р = 1 – α
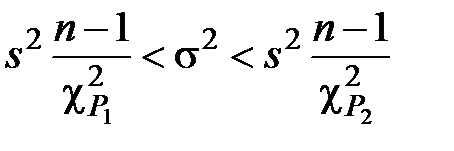 . (2.28)
. (2.28)
Обычно принимают Р1 = α/2 и Р2 = 1 – Р1 = 1 – α/2.
Границы доверительных интервалов для генерального среднего квадратического отклонения σ находят путём извлечения квадратного корня из значений доверительных границ для генеральной дисперсии.
Пример 2.6. По результатам примера 2.1 определить 90 %-ные доверительные интервалы для генеральных дисперсии и среднего квадратического отклонения, если s2 = 126,9 (см. пример 2.1).
По таблице 2.9 для k = n – 1 = 19 находим
χ0,052 = 30,1;
χ0,952 = 10,1.
На основании (2.28)
126,9 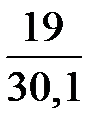 < σ2 < 126,9
< σ2 < 126,9 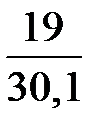 ;
;
80,1 < σ2 < 238,8;
8,95 < σ < 15,5.
В случае цензурированной выборки доверительный интервал для генерального среднего квадратического отклонения приближённо определяют из выражения
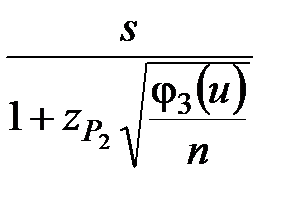 < σ <
< σ < 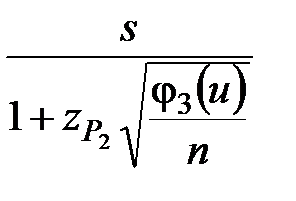 . (2.29)
. (2.29)
Пример 2.7. В условиях примера 2.2 определить 90 %-ные доверительные интервалы для генерального среднего квадратического отклонения значения логарифма, если s = 0,301 и u = = –0,552 (см. пример 2.2)
Для α = 0,1 по таблице 2.7 находим
z0,05 = – 1,64
z0,95 = 1,64
φ3(u) = φ3(–0,552) = 0,8066.
На основании (2.35)
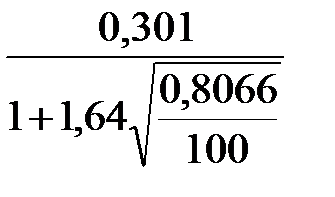 < σ <
< σ < 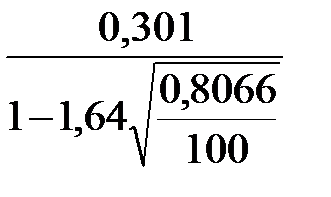 ;
;
0,2624 < σ < 0,353.
Таблица 2.9 – Значения квантили χα2 в зависимости от уровня вероятности и числа свободы k
| k | Вероятность P(χ2 > χα2) | ||||||
| 0,995 | 0,99 | 0,975 | 0,95 | 0,90 | 0,75 | 0,50 | |
| 0,000039 0,010 0,072 0,207 0,412 0,676 0,989 1,34 1,74 2,16 2,60 3,07 3,56 4,08 4,60 5,14 5,70 6,26 6,84 7,43 8,03 8,64 9,26 9,89 10,5 11,2 11,8 12,5 13,1 13,8 | 0,00016 0,020 0,115 0,297 0,554 0,872 1,24 1,65 2,09 2,56 3,05 3,57 4,11 4,66 5,23 5,81 6,41 7,02 7,63 8,26 8,90 9,54 10,2 10,9 11,5 12,2 12,9 13,6 14,3 15,0 | 0,00098 0,051 0,216 0,484 0,831 1,24 1,69 2,18 2,70 3,25 3,82 4,40 5,01 5,63 6,26 6,91 7,56 8,23 8,91 9,59 10,3 11,0 11,7 12,4 13,1 13,8 14,6 15,3 16,0 16,8 | 0,0039 0,103 0,352 0,711 1,15 1,64 2,17 2,73 3,32 3,94 4,58 5,23 5,89 6,57 7,26 7,96 8,67 9,39 10,1 10,9 11,6 12,3 13,1 13,8 14,6 15,4 16,2 16,9 17,7 18,5 | 0,016 0,211 0,584 1,06 1,61 2,20 2,83 3,49 4,17 4,86 5,58 6,30 7,04 7,79 8,55 9,31 10,1 10,9 11,6 12,4 13,2 14,0 14,8 15,7 16,5 17,3 18,1 18,9 19,8 20,6 | 0,101 0,575 1,21 1,92 2,67 3,46 4,26 5,07 5,90 6,74 7,58 8,44 9,30 10,2 11,0 11,9 12,8 13,7 14,6 15,4 16,3 17,2 18,1 19,0 19,9 20,8 21,8 22,7 23,6 24,5 | 0,455 1,39 2,37 3,36 4,35 5,35 6,35 7,34 8,34 9,34 10,3 11,3 12,3 13,3 14,3 15,3 16,3 17,3 18,3 19,3 20,3 21,3 22,3 23,3 24,3 25,3 26,3 27,3 28,3 29,3 |
Окончание таблицы 2.9
| k | Вероятность P(χ2 > χα2) | |||||
| 0,25 | 0,10 | 0,05 | 0,025 | 0,01 | 0,005 | |
| 1,32 2,77 4,11 5,38 6,63 7,84 9,04 10,2 11,4 12,6 13,7 14,8 16,0 17,1 18,3 19,4 20,5 21,6 22,7 23,8 24,9 26,0 27,1 28,2 29,3 30,4 31,5 32,6 33,7 34,8 | 2,71 4,60 6,25 7,78 9,24 10,6 12,0 13,4 14,7 16,0 17,3 18,6 19,8 21,1 22,3 23,5 24,8 26,0 27,2 28,4 29,6 30,8 32,0 33,2 34,4 35,6 36,7 37,9 39,1 40,3 | 3,48 5,99 7,82 9,49 11,1 12,6 14,1 15,5 16,9 18,3 19,7 21,0 22,4 23,7 25,0 26,3 27,6 28,9 30,1 31,4 32,7 33,9 35,2 36,4 37,7 38,9 40,1 41,3 42,6 43,8 | 5,02 7,38 9,35 11,1 12,8 14,4 16,0 17,5 19,0 20,5 21,9 23,3 24,7 26,1 27,5 28,9 30,2 31,5 32,8 34,2 35,5 36,8 38,1 39,4 40,6 41,9 43,2 44,5 45,7 47,0 | 6,64 9,21 11,3 13,3 15,1 16,8 18,5 20,1 21,7 23,2 24,7 26,2 27,7 29,1 30,6 32,0 33,4 34,8 36,2 37,6 38,9 40,3 41,6 43,0 44,3 45,6 47,0 48,3 49,5 50,9 | 7,88 10,6 12,8 14,9 16,8 18,6 20,3 22,0 23,6 25,2 26,8 28,3 29,8 31,3 32,8 34,3 35,7 37,2 38,6 40,0 41,4 42,8 44,2 45,6 46,9 48,3 49,6 51,0 52,3 53,7 |
Если из нормально распределённой генеральной совокупности испытано m выборок объемом n каждая и для каждой выборки подсчитан размах варьирования Ri, то доверительные интервалы для генерального среднего квадратического отклонения можно подсчитать по формуле
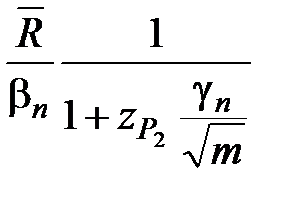 < σ <
< σ < 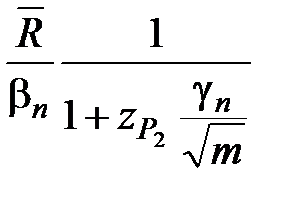 , (2.30)
, (2.30)
где 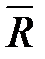 =
= 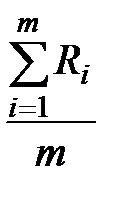 – среднее арифметическое из m размахов.
– среднее арифметическое из m размахов.
Доверительные границы, вычисленные на основе (2.28), несколько уже, чем на основе (2.30).
