Прямое произведение множеств

Используя понятие кортежа, можно определить ещё одну, очень важную для приложений теоретико-множественную операцию – операцию прямого произведения. Прямым произведе-нием множеств X и Y называется множество, состоящее из всех тех и только тех пар, первая компонента каждой из которых принадлежит X, а вторая - Y. Прямое произведение множеств X и Y, рассматриваемых в указанном порядке, обозначается знакосочетанием X´Y. Обратим вни-мание, что пока определено только прямое произведение двух множеств. Заметим также, что прямое произведение двух множеств является множеством кортежей длины 2, т.е. множеством пар.

Пример 2. Пусть A = {m, n}, B = {p, q}, C = {s, t}. ТогдаA´B = {ám, pñ, án, pñ, ám, qñ, án, qñ}; B´C = {áp, sñ, áp, tñ, áq, sñ, áq, tñ}. Далее, (A´B)´C = {áám, pñ, sñ, áán, pñ, sñ, áám, qñ, sñ, áán, qñ, sñ, áám, pñ, tñ, áán, pñ, tñ, áám, qñ, tñ, áán, qñ, tñ}; A´(B´C) = {ám, áp, sññ, ám, áp, tññ, ám, áq, sññ, ám, áq, tññ, án, áp, sññ, án, áp, tññ, án, áq, sññ, án, áq, tññ}. Заметим, что (A´B) ´C ≠ A´ (B´C), поскольку эти множества состоят из разных объектов; в частности, их первые компоненты áám, pñ, sñ и ám, áp, sññ не равны друг другу ■

Тем не менее понятие прямого произведения легко распространяется на любое конечное число множеств. Пусть {Х_i} (1 ≤ i ≤ n) - конечное семейство множеств. Прямым произведени-ем семейства множеств называется множество, состоящее из всех тех и только тех кортежей длины n, первая компонента каждого из которых принадлежит X₁, вторая - Х₂, ..., n-ая - Х_n. Прямое произведение указанного семейства обозначается знакосочетанием X₁´Х₂´ ... ´Х_n, или, короче, . Если в семействе {Х_i} (1 ≤ i≤ n) все множества одинаковы и равны, например, множеству М, то прямое произведение этого семейства называется n-й степенью множества М и обозначается через М ⁿ. По определению полагают M¹ = M, M⁰ = L.

Пример 3. Пусть, как и в примере 2, A = {m, n}, B = {p, q}, C = {s, t}. Тогда A´B´C = {ám, p, sñ, án, p, sñ, ám, q, sñ, án, q, sñ, ám, p, tñ, án, p, tñ, ám, q, tñ, án, q, tñ}, т.е. это множество кортежей длины 3. Естественно, что A´B´C ≠ (A´B)´C и A´B´C ≠ A´(B´C) ■

Пример 4. Пусть A = {a, b, c}, B = {p, q}, C = {a, q}. Найти (A×В)×С, A×(В×С) и A×В×С.

По определению прямого произведения A×В = {áa, pñ, áa, qñ, áb, pñ, áb, qñ, ác, pñ, ác, qñ}, В×С =

{áp, añ, áp, qñ, áq, añ, áq, qñ}. Далее,

(A×В)×С = {ááa, pñ, añ, ááa, pñ, qñ, ááa, qñ, añ, ááa, qñ, qñ, ááb, pñ, añ, ááb, pñ, qñ, ááb, qñ, añ, ááb, qñ, qñ, áác, pñ, añ, áác, pñ, qñ, áác, qñ, añ, áác, qñ, qñ};

A×(В×С) = {áa, áp, aññ, áa, áp, qññ, áa, áq, aññ, áa, áq, qññ, áb, áp, aññ, áb, áp, qññ, áb, áq, aññ, áb, áq, qññ, ác, áp, aññ, ác, áp, qññ, ác, áq, aññ, ác, áq, qññ};

A×В×Сñ = {áa, p, añ, áa, p, qñ, áa, q, añ, áa, q, qñ, áb, p, añ, áb, p, qñ, áb, q, añ, áb, q, qñ, ác, p, añ, ác, p, qñ, ác, q, añ, ác, q, qñ}.

Следует обратить внимание на то, что 1-ое и 2-ое множества являются множествами кортежей длины 2, в то время как 3-ье множество является множеством кортежей длины 3 ■

Операция проектирования

Используя введенные понятия, определим еще одну теоретико-множественную операцию - проектирование, применяемую только к множеству кортежей одинаковой длины. Поскольку проекция множества кортежей определяется через проекцию кортежа, начнем с её определения.

Пустьa = áa₁, a₂, ..., a_sñ-кортеж длины s > 0.

1) Проекцией кортежа a на i-ю ось называется и через ПР_ia обозначается i-я компонента кор-тежа a, т.е. a_i. Таким образом, ПР_ia = a_i (i = 1, …, s).

2) Пусть 2 ≤ q ≤ s и 1 ≤ i₁<i₂< ... <i_q-1<i_q ≤ s. Проекцией кортежа a на оси с номерами i₁, i₂, ..., i_q называется и через α обозначается кортеж á ñ. Таким образом, α = á ñ.

3) Проекцией кортежа a на пустое множество осей называется и через ПР_Æa обозначается пустой кортеж L. Таким образом, ПР_Æa = L.

4) Проекцией пустого кортежа L на пустое множество осей называется и через ПР_ÆL обоз-начается пустой кортеж L. Таким образом, ПР_ÆL = L.

Пример 5.Если α = áx, yñ, то ПР₁a = x, ПР₂a = y. Если α = á{x}, áyññ, то ПР₁a = {x}, ПР₂a = áyñ. Если α = ááx, áyññ, xñ, то 1-ой компонентой кортежа α является кортеж áx, áyññ длины 2, а его 2-ой компонентой – элемент x, т.е. ПР₁a = áx, áyññ, ПР₂a = x ■

Определим теперь понятие «проекция множества». Как уже было указано выше, это поня-тие будет определено только для того случая, когда проектируемое множество состоит из кор-тежей, причем все эти кортежи имеют одинаковую длину.

Пусть М - множество кортежей длины s > 0. Поскольку пустое множество Æ не является множеством кортежей длины s > 0, то множество М предполагается непустым.

1) Проекцией множества М на i-ю ось называется и через ПР_iМ обозначается множество проекций кортежей из М на i-ю ось (i = 1, …, s).

2) Пусть 2 ≤ q ≤ s и 1 ≤ i₁<i₂< ... <i_q-1<i_q ≤ s. Проекцией множества М на оси с номерами i₁, i₂,

..., i_q называется и через M обозначается множество проекций кортежей из М на оси с

номерами i₁, i₂, ..., i_q-1, i_q.

3) Проекцией множества М на пустое множество осей называется и через ПР_ÆМ обознача-ется пустой кортеж L. Таким образом, ПР_ÆМ = L.

Пример 6.Пусть М = {áa, p, qñ, áa, q, qñ, áb, p, qñ, áb, q, añ, áb, q, qñ, ác, p, añ, ác, p, qñ, ác, q, qñ}. Найдём проекцию ПР₂₃ заданного множества М кортежей на оси с номерами 2 и 3. По опре-делению проекции множества, ПР₂₃М состоит из всех проекций всех кортежей из М на указан-ные оси. Из определения проекции кортежей, проекция отдельного кортежа a – это просто кор-теж, состоящий из компонент a с соответствующими номерами. Так, для 1-го по порядку корте-жа из М – áa, p, qñ – его проекцией ПР₂₃ áa, p, qñ на оси 2, 3 будет кортеж (длины 2) áp, qñ. Далее, ПР₂₃áa, q, qñ = áq, qñ, и т.д. В результате получаем: ПР₂₃М = {áp, qñ, áq, qñ, áq, añ, áp, añ}. Здесь в проектируемом множестве М 8 кортежей, а в проекции – 4. Это происходит потому, что проек-ции различных кортежей из исходного множества совпадают. Например, ПР₂₃ áa, q, qñ = ПР₂₃ áс, q, qñ = áq, qñ ■

Пример 7. Пусть A и В – два произвольных множества, М = A × В. По определению опера-ций прямого произведения и проектирования имеем ПР₁М = A, ПР₂М = В. Поэтому можно ска-зать, что операции прямого произведения и проектирования являются взаимно-обратными (не уточняя этого понятия) ■

Пример 8.Пусть М – множество точек áx, yñ на плоскости, удовлетворяющих условию x²+ y² = 1 (т.е. М – это окружность единичного радиуса с центром в начале координат). Нетрудно видеть, что по определению проекции ПР₁М = ПР₂М = [–1, 1] (так обозначен отрезок с концами –1 и 1). Таким образом, для геометрических фигур на плоскости (подмножеств двумерного евклидова пространства E²), состоящих из двумерных точек – кортежей длины 2, введённая здесь операция проектирования совпадает с хорошо известной операцией проектирования вдоль координатных осей в геометрии ■

Далее будут рассмотрены понятия, которые, в отличие от рассмотренных выше исходных понятий высказывания, множества и кортежа, будут формально определены – через эти, ранее введённые неопределяемые понятия.

Графики

Одним из важнейших понятий дискретной – и не только дискретной – математики явля-ется понятие графика. График - это множество пар, т.е. множество, элементами которого служат пары. Вспоминая (см. раздел 1), что пара – это кортеж длины 2, можно сказать, что гра-фиком называется любое множество кортежей длины 2. Как и рассмотренное в разделе 3 поня-тие проектирования, понятия графика также является обобщением хорошо известного «школь-ного» понятия графика функции.

Пример 9.Вспомним хорошо известный график функции y = sinx. По построению, такой график состоит из всех пар чисел áx, yñ (точек), таких, что y = sinx. Поэтому, как и любое мно-жество точек на плоскости, график данной функции является графиком и в смысле введённого определения, т.е. он является множеством пар ■

Заметим, что множества точек на плоскости из примеров 8 и 9 являются бесконечными. Они задаются не перечислением, а условиями на принадлежащие им элементы – набором характеристических свойств, т.е. таким набором свойств, которым обладают только элементы рассматриваемого множества. Подробнее такой способ задания множеств будет рассмотрен далее, в разделе 4-2.1.

Областью определения графика G называется множество ПР₁G, а областью значений графика G - множество ПР₂G. Таким образом, нахождение областей определения и значений графика сводится к операции проектирования кортежей длины 2 на одну из двух осей. Эта опе-рация является частным случаем операции проектирования (проектирование на одну ось), рас-смотренной в разделе 3.

4.1.Операции над графиками. Рассмотрим две важные операции над графиками: одно-местную - инверсию, и двухместную - композицию. Инверсия графика определяется через ин-версию пары. Пара áс, dñ называется инверсией пары áa, bñ, eсли с = b, d = а. Другими словами, инверсией пары áa, bñ является пара áb, añ. Инверсия пары a обозначается через a^-1. Легко ви-деть, что (a^-1)^-1 = a. Инверсией графика G называется множество инверсий всех пар из G. Ин-версия графика G обозначается через G^-1. График называется симметрическим, если G = G^-1. Для симметрических графиков истинны следующие два высказывания: aÎGDaÎG^-1 и aÎGD a^-1ÎG (напомним, что знаком D обозначена определённая в разделе 1-2.1.5 операция «эквива-лентность» над истинностными значениями высказываний). Легко видеть также, что истин-ность любого из этих двух высказываний влечёт равенство G = G^-1.

Пример 10.Пусть X – произвольное множество. Рассмотрим множество X^D всех пар вида áx, xñ, где хÎX. Легко видеть, что X^D – симметрический график. Он называется диагональю множества X².

Введём необходимые понятия. Пусть α = áp, qñ, β = ás, tñ – две пары. Композицией α○β пар α и β (в указанном порядке) называется пара γ, определяемая следующим образом:

γ = , (1)

где Λ – пустой кортеж (см. раздел 1.1).

Пример 11.Композицией пар α = áp, qñ и β = áq, rñ при любых p, q и r в соответствие с формулой (1) является пара γ = áp, rñ. Композицией пар β = áq, rñ и α = áp, qñ при p = r является пара áq, qñ. Композицией пар β = áq, rñ и α = áp, qñ при p ≠ rявляется пустой кортеж Λ. Компози-цией пар α = ááp, rñ, qñ и β = áq, rñ является пара ááp, rñ, rñ. Действительно, формула (1) при q = s определяет пару áp, tñ при произвольных p и t. В данном случае на первом месте (вместо p) сто-ит пара áp, rñ, а на втором месте (вместо t) стоит элемент r. Ещё раз почеркнём, что компонен-тами кортежа могут быть любые объекты, включая множества и другие кортежи ■

Исходя из операции композиции двух пар, введём теперь операцию композицию двух графиков, т.е. множеств пар (см. определение графика). Композиция R= P○Q определяется как множество композиций всех пар из P со всеми парами из Q. Формально:

P Q = , (2)

где композиция двух пар α○β определена формулой (1).

Пример 12.Пусть график P = {áa, bñ, áa, cñ}, график Q= {áb, bñ, ád, cñ}. Найдём компози-цию графиков P○Q. Имеем в соответствии с формулой (2) P○Q = {áa, bñ○áb, bñ, áa, bñ○ád, cñ, áa,cñ○áb, bñ, áa, cñ○ád, cñ}. В соответствии с формулой (1) для композиций двух пар имеем

áa, bñ○áb, bñ = áa, bñ, áa, bñ○ád, cñ = áa, cñ○{áb, bñ = áa, cñ○ád, cñ = Λ.

Поэтому P○Q = {áa, bñ} (множество пар из P○Q состоит из одной пары áa, bñ).

Найдём теперь композицию графиковQ○Pпри тех же самых Q и P. Имеем Q○P = {áb, bñ○áa, bñ, áb, bñ○áa,cñ, ád, cñ○áa, bñ, ád, cñ○áa, cñ} = Λ. В этом порядке композиция оказалась пустой ■

Для бесконечных графиков формула (2) остаётся в силе, однако непосредственное рас-смотрение всех пар из P и Q(как это делается в примере 12) невозможно. Однако для нахожде-ния композиции P○Qможно воспользоваться следующим простым соображением, справедли-вым для произвольных графиков.

Утверждение 1. Пара áx, yñÎP○Q тогда и только тогда, когда существует элемент z, такой, что áx, zñÎP и áz, yñÎQ ■

Пример 13.Рассмотрим композицию двух графиков P и Q: y = sinx и y = lnx. В соответст-вии с вышесказанным, пара чисел áx, yñÎP○Q тогда и только тогда, когда существует элемент z, такой, что z = sinx и y = lnz. В данном случае это означает, что ln(sinx) определён, что может быть при любом x, для которого sinx> 0. А для последнего необходимо и достаточно, чтобы вы-полнялось условие 2kπ<x<(2k+1)π для какого-нибудь целого числа k. Соответствующее значе-ние y из пары áx, yñÎP○Q определяется формулой y = ln(sinx) ■

Пример 13 показывает, что достаточно сложное – на первый взгляд – понятие композиции двух графиков является обобщением хорошо известного «школьного» понятия суперпозиции двух функций.

Если у нас имеется три графика: P, Q и R, то с помощью операции композиции двух гра-фиков из них можно определить два разных графика: (P○Q)○R и (P○(Q○R). Имеет место

Утверждение 2. Графики (P○Q)○R и P○(Q○R) совпадают, т.е. состоят из одних и тех же пар ■

Утверждение 2 выражает важное свойство операции композиции – её ассоциативность. Это означает, что в выражениях (P○Q)○R и P○(Q○R), как и в более сложных выражениях такого же типа, можно убрать скобки и рассматривать композицию не только двух, но и любого числа графиков: P○Q○R, P○Q○R○S, и т.д.

4.2. Свойства графиков.График называется функциональным (инъективным), если в нем нет пар с одинаковыми первыми (соответственно одинаковыми вторыми) компонентами.

Пример 14.График {áb, bñ, áa, nñ} является функциональным и инъективным, поскольку в обеих входящих в него парах и первые, и вторые компоненты являются разными: b≠a (первые компоненты) и b≠n (вторые компоненты). Заметим, что совпадение компонент в паре áb, bñ ни-как не влияет на рассматриваемые свойства. График {áx, bñ, áx, añ} не является функциональ-ным, но является инъективным (первые компоненты совпадают, а вторые – нет). График {án, сñ, ád, cñ} является функциональным, но не является инъективным (вторые компоненты совпадают, а первые – нет). Наконец, график {án, bñ, án, сñ, ád, cñ}, состоящий из трёх пар, не является ни функциональным (поскольку он содержит пары án, bñ и án, сñ с совпадающими первыми компонентами), ни инъективным (поскольку он содержит пары án, сñ и ád, cñ с совпадающими вторыми компонентами) ■

Пример 15.Рассмотрим график, состоящий из всех точек áx, yñ, удовлетворяющих уравне-нию окружности x² + y² = 1. Этот график не является ни функциональным (поскольку он содер-жит пары á0, 1ñ и á0, –1ñ с совпадающими первыми компонентами), ни инъективным (поскольку он содержит пары á1, 0ñ и á–1, 0ñ с совпадающими вторыми компонентами) ■

Пример 16.Рассмотрим график, состоящий из всех точек áx, yñ, удовлетворяющих уравне-нию y = ln(x). Этот график является функциональным и инъективным, поскольку он является графиком строго возрастающей функции (т.е. (x₁ ≠ x₂) D (y₁ ≠ y₂)) ■

Соответствия и функции

Соответствием называется тройка, первая компонента которой есть подмножество пря-мого произведения множеств, являющихся ее второй и третьей компонентами. Обратим внима-ние на то, что все объекты, участвующие в этом определении – тройка, компонента, подмно-жество, прямое произведение, множество – ранее уже были введены и объяснены. В то же вре-мя приведённое определение не включает в себя понятий зависимой и независимой перемен-ной, закона, правила (по которым находится значение зависимой переменной, соответствующее данному значению независимой), и других нуждающихся в объяснении понятий.

Соответствия будут обозначаться прописными греческими буквами. Таким образом, если Г = áG, X, Yñ – соответствие, то, в согласии с определением, X, Y – множества, a G 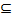X×Y. По построению, G является графиком, поскольку G – подмножество прямого произведения двух множеств, которое по определению является множеством пар (см. раздел 1.2). Множество G называется графиком соответствия Г. Множества X и Y носят название области отправле-ния и области прибытия соответствия Г. Множество ПР₁G называется областью определе-ния соответствия Г_, a множество ПР₂G – областью значений соответствия Г (определения проекции см. в разделе 1.3).

Если пара áx, yñ G, тo говорят, что элемент у соответствует элементу x в (или при) соот-ветствии Г. Если x ПР₁G, тoговорят, что соответствие Г определено на элементе x. Элемент у называется также образом элемента x в (или при) соответствии Г.

Инверсией соответствия Г = áG, X, Yñ называется и через Г⁻¹ обозначается соответствие áG⁻¹, Y, Xñ, где G⁻¹– инверсия графика G (см. начало раздела 4.1). Ясно, что (Г⁻¹)⁻¹ = Г. Если Г = áG, X, Yñ и Δ =áH, U, Vñ – соответствия, то соответствие Σ = áG○H, X, Vñ называется их ком-позицией и обозначается через Г○Δ. Из ассоциативности композиции графиков следует ассоци-ативность композиции соответствий.

Сужением соответствия Г = áG, X, Yñ на множество А называется и через Г_А обозна­чается соответствие áG∩(А´Y), X, Yñ. Обратим внимание, что области отправления и прибытия соответствия не меняются. Соответствие Δ =áH, Z, Uñ называется продолжением соответст-вия Г = áG, X, Yñ, если GÍH, XÍZ, YÍU.

Введём ещё одно понятие, связанное с графиками и соответствиями. Пусть G – произволь-ный график. Введём в рассмотрение соответствие графика G: Г_G = áG, ПР₁G, ПР₂Gñ (напом-ним, что через ПР₁G и ПР₂G обозначены проекции графика G). У соответствия Г_G область отправления совпадает с областью определения, а область прибытия – с областью значений. Бо-лее того, имеет место простое

Утверждение 3. Любое соответствие с графиком G является продолжением соответствия Г_G.

Соответствие называется функциональным, или функцией, если его график функциона-лен; инъективным, если его график инъективен; всюду определенным, если его область оп­ределения совпадает с областью отправления, и сюръективным, если его область прибытия совпадает с областью значений.

Соответствие, обладающее четырьмя перечисленными свойствами, называется взаимно-однозначным, или биективным, или биекцией.

Функция Г с областью отправления X и областью прибытия Y называется функцией типа X→Y. Напомним, что образом элемента x называется единственный (в силу фунциональности Г) элемент y, такой, что пара áx, yñÎG. Образ y элемента x при функции Г обозначается через Г(x). Это уже близко к привычному обозначению y = f(x). Для поного «возвращения» к школь-ным понятиям необходимо дать аккуратное описание термина «переменная». С этого и будет начинаться следующая глава.

Задания

Задание 1. См. примеры 2, 3, 4 для образца.

01. Пусть A = {a, b, c}, B = {ápñ, q}, C = {a, q}. Найти (A×В)×С и A×В×С.

02. Пусть A = {a, b, c}, B = {p, q}, C = {a, q}. Найти A×(В×С) и A×В×С.

03. Пусть A = {áp, qñ, m}, B = {m, a}, C = {a, q}. Найти (A×В)×С и A×В×С.

04. Пусть A = {áp, qñ, m}, B = {m, a}, C = {q, a}. Найти A×(В×С) и A×В×С.

05. Пусть A = {p, áq, mñ}, B = {m, a}, C = {a, q}. Найти (A×В)×С и A×В×С.

06. Пусть A = {a, c}, B = {b,p, q}, C = {a, q}. Найти A×(В×С) и A×В×С.

07. Пусть A = {a, c}, B = {b,p, q}, C = {a, q}. Найти (A×В)×С и A×В×С.

08. Пусть A = {a, c}, B = {b,p, q}, C = {a, q}. Найти (A×В)×С и A×(В×С).

09. Пусть A = {a, b, c}, B = {p, q}, C = {a, p, q}. Найти A×(В×С) и A×В×С.

10. Пусть A = {a, b, c}, B = {p, q}, C = {a, p, q}. Найти A×В)×С и A×В×С.

11. Пусть A = {a, b, c}, B = {p, q}, C = {a, p, q}. Найти (A×В)×С и A×(В×С).

12. Пусть A = {a, c}, B = {b,p, q}, C = {q}. Найти A×(В×С) и A×В×С.

13. Пусть A = {a}, B = {b,p, q}, C = {a, q}. Найти (A×В)×С и A×В×С.

14. Пусть A = {a, c}, B = {b,p}, C = {a, q}. Найти (A×В)×С и A×(В×С).

15. Пусть A = {b, c}, B = {b, q}, C = {a, p, q}. Найти A×(В×С) и A×В×С.

16. Пусть A = {a, b}, B = {p, q}, C = {a, p, q}. Найти A×В)×С и A×В×С.

17. Пусть A = {a, b, c}, B = {b}, C = {b, q}. Найти (A×В)×С и A×(В×С).

18. Пусть A = {a, b, m}, B = {m, q}, C = {p, q}. Найти A×В)×С и A×В×С.

19. Пусть A = {a, m}, B = {m, q}, C = {a, m, q}. Найти (A×В)×С и A×(В×С).

20. Пусть A = {a, c}, B = {b,p, q}, C = {r, m}. Найти A×(В×С) и A×В×С.

21. Пусть A = {áp, qñ, m}, B = {m, a}, C = {a, q}. Найти (A×В)×С и A×В×С.

22. Пусть A = {áp, qñ, m}, B = {m, a}, C = {q, a}. Найти A×(В×С) и A×В×С■

Задание 2. См. примеры 5, 6 для образца.

01. Пусть М = {áa, p, qñ, áa, q, qñ, áb, q, pñ, áb, q, añ, áb, q, qñ, ác, p, añ, ác, p, qñ, ác, q, qñ}. Найти проекцию ПР₁₃ заданного множества М кортежей на оси с номерами 1 и 3.

02. Пусть М = {áa, p, qñ, áa, q, qñ, áb, p, qñ, áb, q, añ, áb, q, qñ, ác, p, añ, ác, p, qñ, ác, b, qñ}. Найти проекцию ПР₁₂ заданного множества М кортежей на оси с номерами 1 и 2.

03. Пусть М = {áa, p, qñ, áa, q, qñ, áb, p, qñ, áb, q, añ, áb, q, qñ, ác, p, añ, ác, p, qñ, ác, q, qñ}. Найти проекцию ПР₂₃ заданного множества М кортежей на оси с номерами 2 и3.

04. Пусть М = {áa, p, qñ, áa, q, qñ, áb, q, añ, áb, q, qñ, ác, p, añ, ác, p, qñ, ác, q, qñ}. Найти проекцию ПР₁₃ заданного множества М кортежей на оси с номерами 1 и 3.

05. Пусть М = {áa, p, qñ, áa, q, qñ, áb, p, qñ, áb, q, añ, áb, q, qñ, ác, p, añ, ác, q, qñ}. Найти проекцию ПР₁₂ заданного множества М кортежей на оси с номерами 1 и 2.

06. Пусть М = {áa, p, qñ, áb, p, qñ, áb, q, añ, áb, q, qñ, ác, p, añ, ác, p, qñ, ác, q, qñ}. Найти проекцию ПР₂₃ заданного множества М кортежей на оси с номерами 2 и3.

07. Пусть М = {áa, p, qñ, áb, p, qñ, áb, q, añ, áb, q, qñ, ác, p, añ, ác, p, qñ, ác, q, qñ}. Найти проекцию

ПР₁₂ заданного множества М кортежей на оси с номерами 1 и 2.

08. Пусть М = {áa, p, qñ, áa, q, qñ, áb, b, qñ, áb, q, añ, áb, q, qñ, ác, p, añ, áq, p, qñ, ác, q, qñ}. Найти проекцию ПР₂₃ заданного множества М кортежей на оси с номерами 2 и3.

09. Пусть М = {áa, p, pñ, áa, q, qñ, áb, q, añ, áb, q, qñ, ác, p, añ, ác, a, qñ, ác, q, qñ}. Найти проекцию ПР₁₃ заданного множества М кортежей на оси с номерами 1 и 2.

10. Пусть М = {áa, p, qñ, áa, q, qñ, áb, p, qñ, áq, q, añ, áb, q, qñ, ác, p, añ, ác, c, qñ}. Найти проекцию ПР₁₂ заданного множества М кортежей на оси с номерами 1 и 3 ■

Задание 3.Найти области определения и значения следующих графиков.

01. y = sinx.

02. {áp, qñ, áq, qñ, áq, añ, áp, añ}.

03. y = arcsinx.

04. {áa, cñ, áb, pñ, áq, fñ, á{a}, áqññ}.

05. y = tgx.

06. {áb, xñ, áa, nñ, áx, bñ, ád, añ}.

07. y = arcctgx.

08. {áx, xñ, ál, añ, áx, bñ}.

09. y = ln(1- x²).

10. {áb, cñ,áb, bñ, ád, cñ}■

Задание 4.Найти инверсии следующих графиков.

01. {áa, bñ, án, cñ, áb, qñ}.

02. {áa, dñ, áb, cñ, áb, bñ}.

03. {áb, bñ, ál, nñ, án, bñ}.

04. {áx, zñ, áa, lñ, áx, yñ, áz, xñ}.

05. {áb, nñ, ár, pñ, ám, bñ, áp, bñ} ■

Задание 5.Найти композицию пар в указанном и обратном порядке. См. пример 11 для образца:

01. án, cñ○ác, cñ.

02. áa, dñ○áb, bñ.

03. áa, bñ○áb, añ.

04. áb, añ○áa, bñ.

05. ál, nñ○án, bñ.

06. án, bñ○ál, nñ.

07. áb, xñ○áx, fñ.

08. áb, xñ○áx, áfññ.

09. á{b}, xñ○áx, fñ.

10. áb, xñ○áy, fñ■

Задание 6.Найти композицию пар в указанном и обратном порядке. См. пример 12 для образца:

01. P = {áa, bñ, án, cñ}, Q = {áb, nñ, ác, cñ}.

02. P = {áa, dñ, áb, cñ},Q = {áb, bñ, ád, cñ}.

03. P = {áa, xñ, áx, xñ},Q = {áx, bñ, áb, añ}.

04. P = {áy, dñ, áy, cñ},Q = {ác, bñ, áz, yñ}.

05. P = {áa, bñ, áa, cñ}, Q = {áb, bñ, ád, cñ}.

06. P = {áb, nñ, ál, nñ}, Q = {án, bñ, ád, cñ}.

07. P = {án, bñ, ác, nñ}, Q = {án, bñ, áb, cñ}.

08. P = {áa, bñ, áa, cñ}, Q = {áb, bñ, ád, añ}.

09. P = {áa, bñ, án, cñ},Q = {áb, nñ, ác, cñ}.

10. P = {áb, bñ, ál, nñ}, Q = {án, bñ, ád, lñ}.

11. P = {áa, añ, áa, cñ}, Q = {áb, añ, ác, añ}.

12. P = {áb, xñ, áa, nñ}, Q = {áx, bñ, ád, añ}.

13. P = {áx, xñ, ál, añ}, Q = {áx, fñ, áy, xñ}.

14. P = {áb, bñ, áa, lñ}, Q = {áx, bñ, ál, añ}.

15. P = {ár, nñ, ár, rñ}, Q = {ám, bñ, ád, rñ}.

16. P = {áb, xñ, áa, nñ}, Q = {áb, bñ, áp, qñ}.

17. P = {áx, xñ, áa, lñ}, Q = {áx, yñ, áy, xñ}.

18. P = {áb, bñ, áa, nñ}, Q = {áx, yñ, áb, añ}.

19. P = {áb, nñ, ál, nñ}, Q = {áx, bñ, án, añ}.

20. P = {áb, xñ, áa, nñ}, Q = {án, bñ, ád, cñ}.

21. P = {áx, xñ, ál, añ}, Q ={áx, bñ, ál, bñ}.

22. P = {áf, bñ, áa, lñ}, Q = {áx, fñ, áy, xñ}.

23. P = {áb, nñ, ár, pñ}, Q = {ám, bñ, áp, bñ}.

24. P = {áb, xñ, áq, nñ}, Q = {ád, rñ, áp, qñ}.

25. P = {áx, zñ, áa, lñ}, Q = {áx, yñ, áz, xñ}.

26. P = {áb, bñ, áa, nñ}, Q = {áx, bñ, áa, añ}.■

Задание 7.Для всех графиков из заданий 3, 4 и 6 проверить наличие (или отсутствие) свойств функциональности и инъективности (см. примеры 14 – 16) ■

Задание 8. Для всех графиков из задания 6 найти проекции ПР₁G, ПР₂G. См. примеры 6 – 8 для образца ■

Предметный указатель

График

инъективный

симметрический

функциональный

Графика,

инверсия

область определения

область значений

соответствие

Графиков

композиция

Кортеж

над множеством

Кортежа,

длина

компонента

проекция,

на i-ю ось

на оси с номерами i₁, i₂, ..., i_q

на пустое множество осей

Множества диагональ

Множества кортежей,

проекция

наi-ю ось

на оси с номерами i₁, i₂, ..., i_q

на пустое множество осей

Образ элемента в (при) соответствии

Операции над графиками

Пар, композиция

Пара

Пары инверсия

Проектирования операция

Прямое произведение,

двух множеств

семейства множеств

Соответствие

биективное

взаимно-однозначное

всюду определенное

инъективное

функциональное

Соответствия,

график

область значений

область определения

область отправления

область прибытия

Тройка

Функция

Функция типа X→Y