Сложные сигналы, манипулированные по фазе двоичной псевдослучайной последовательностью

Для получения сжатия более 13-ти применяют так называемые бинарные кодирующие последовательности максимального периода (ПМП или М-последовательности).

Генерирование псевдослучайных двоичных М-последовательностей осуществляется схемой C-разрядного регистра сдвига (РС) с комбинационной логической схемой (КС) в цепи обратной связи (рис.4.13).

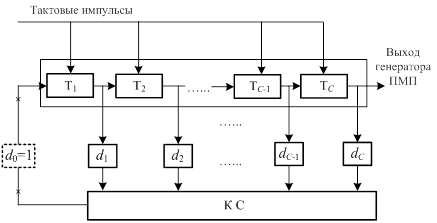
Рис.4.13.

Структура КС выбирается в соответствии с рекуррентным соотношением

d_C X^C Å d_C-1X^C-1Å…Åd₁X¹Å d₀X⁰ =0. (4.3)

В уравнении (4.3) Xⁱ представляют собой выходные сигналы i-х каскадов (триггерных элементов Т_i) регистра сдвига (X⁰ – входной сигнал первого каскада регистра сдвига), которые принимают в фиксированные моменты времени значения 0 или 1. Коэффициенты d_i также равны 0 или 1, причем всегда d₀ = 1, так как сигнал с выхода комбинационной схемы обязательно должен подаваться на вход регистра сдвига, Å – операция сложения по модулю два.

Учитывая свойства операции сложения по модулю два, уравнение (4.3) можно преобразовать в следующее соотношение:

X⁰ = d_C X^C Å d_C-1 X^C-1 Å… Åd₁ X¹, (4.4)

определяющее сумму, которая в каждом такте работы записывается из КС в первый элемент регистра сдвига (РС). Выходные сигналы X¹, X²,…, X^C триггерных элементов Т₁, Т₂, …, Т_С регистра сдвига представляют собой периодические двоичные последовательности символов a₁, a₂,…, a_i,…, a_N, сдвинутых относительно друг друга на один элемент (a_i принадлежит алфавиту (0,1)).

Выходной сигнал i-го триггерного элемента Xⁱ можно выразить через последовательность на выходе (i – k)- го разряда при помощи оператора задержки следующим образом:

Xⁱ =X^i-k D^k, (4.5)

где D – оператор задержки на один такт.

Используя (4.5) , преобразуем рекуррентное соотношение (4.3) к виду:

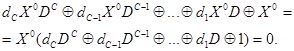
Выражение, стоящее в скобках, представляет собой многочлен степени C относительно D (многочлен задержки). Как показывает анализ, работа формирователя двоичных последовательностей определяется характеристическим многочленом некоторой переменной x, сопряженным с многочленом задержки:

f(x)= x^CÅd₁ x^C-1 Å…Å d_C-1 x Å d_C.

Для того чтобы выходная последовательность имела максимально возможный период 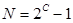, характеристический многочлен должен быть неприводимым и примитивным. Значения коэффициентов характеристических многочленов ПМП до C=7 включительно даны в табл. 1 (где d₀ =d_C =1).

Таблица 1.

№	С	d0	d1	d2	d3	d4	d5	d6	d7

Заметим, что любому набору коэффициентов d_i характеристического многочлена соответствует набор с инверсным расположением коэффициентов , причем

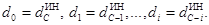
В качестве примера определим структуру формирователя ПМП, соответствующую многочлену, коэффициенты которого приведены в строке 6 табл.1 . Для этого случая C = 5, d₀ = d₁ = d₂ = d₃ = d₅ = 1, d₄ = 0.

Многочлен задержки имеет вид D⁵Å D³Å D²Å DÅ1, а входной сигнал первого регистра сдвига определяется уравнением

X⁰= X⁵Å X³Å X²Å X¹.

Значения коэффициентов неприводимых примитивных многочленов для С >7 можно найти в работах, посвященных применению шумоподобных сигналов в системах связи.

Схема генератора ПМП приведена на рис.4.14.

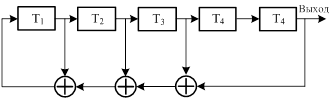
Рис. 4.14.

Для получения М-последовательности в регистр сдвига необходимо записать начальный блок из С двоичных элементов (a₁, a₂,…, a_C), который не может состоять из одних нулей (в противном случае все элементы генерирующей поверхности будут равны нулю). После подачи тактовых импульсов на выходе формирователя образуется двоичная последовательность, первые С элементов которой являются элементами начального блока. Элементы a_C-1,…, a_N получаются в результате выполнения операции суммирования С предыдущих элементов последовательности в соответствии с рекуррентным соотношением (4.4) на каждом последующем такте работы РС. Поэтому для элемента a_i можно записать

a_i=d₁a_i-1 Å d₂ a_i-2 Å…Å d_C a_i-C

или в более компактной форме

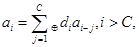(4.6)

где символ å_Å означает суммирование по модулю два.

При расчете корреляционных функций сигналов и ПМП удобно перейти от двоичного алфавита {0,1} к алфавиту {+1,-1}. Тогда операция сложения по модулю два в алфавите {0,1}:

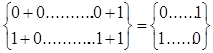
заменяется операцией умножения в алфавите {+1,-1}

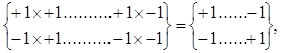
а рекуррентное правило (4.6) получения элементов ПМП преобразуется к виду:

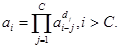(4.7)

М-последовательности обладают рядом свойств, которые и определяют их хорошие корреляционные свойства. Приведем некоторые из них:

– число единиц в М-последовательности на единицу больше числа нулей;

– в М-последовательности содержатся все С-значные комбинации двоичных символов, кроме нулевой;

– сумма по модулю 2 элементов периода повторения М-последовательности с этой же последовательностью, но сдвинутой на любое число элементов, кроме числа, равного периоду, является М-последовательностью того же вида, но имеющей другой сдвиг;

– последовательность, полученная в результате суммирования М- последовательностей различных периодов, также периодична, причем ее период равен наименьшему кратному периодов суммируемых последовательностей;

– при заданном С число различных М-последовательностей Q, т.е. различных правил кодообразования, определяется выражением:

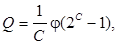
где φ(x) – функция Эйлера, которая определяет количество чисел, включая единицу, меньших x и взаимно простых с x.

Соотношение для вычисления корреляционной функции комплексной огибающей радиосигнала, манипулированного по фазе на два уровня (0, p) в соответствии с ПМП, можно получить из общего выражения для функции неопределенности (3.6), положив f = 0. Если элементарные сигналы, соответствующие одному символу ПМП, имеют прямоугольную огибающую, то нормированная КФ видеосигнала, манипулированного ПМП, определится следующим выражением:

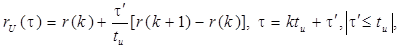
где r(k) – нормированная дискретная корреляционная функция М-последовательности,

k – дискретный временной сдвиг, равный целому числу элементов, на которое сдвинуты кодирующие М- последовательности, k = 0, 1, 2…..

t_u – длительность элементарного сигнала.

Рассмотрим корреляционные функции кодирующих ПМП, используемые на практике:

а) Корреляционная функция непрерывной периодической последовательности вычисляется по формуле:

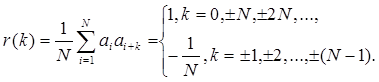
Как видно, нормированная корреляционная функция имеет основной выброс, равный 1, и боковые выбросы, относительный уровень которых равен 1/N (рис.4.15). С ростом N корреляционная функция таких сигналов приближается к идеальной, когда боковые выбросы по сравнению с основными становятся пренебрежительно малыми.

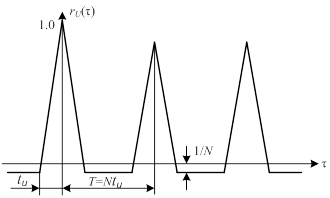
Рис.4.15.

б) Корреляционная функция единичной сигнальной посылки, кодированной периодом ПМП из N элементов:

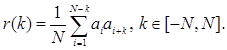
В этом случае корреляционная функция будет иметь наибольшие боковые выбросы, равные примерно 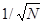, что вытекает из псевдослучайного характера последовательности, в которой содержится приблизительно одинаковое число элементов +1 и –1 (рис.4.16).

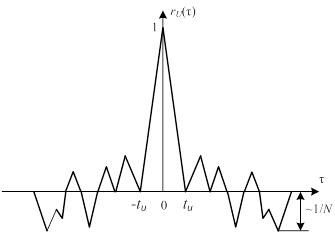
Рис.4.16.

Однако можно найти такие М-последовательности, у которых будет более удачное сочетание разнополярных символов, в результате чего уровень наибольших боковых выбросов может быть меньше 1/N.

в) Корреляционная функция пачки сигнальных посылок, кодированных периодом ПМП из N элементов или усеченным периодом из P элементов (1 ≤ P ≤ N). Число сигнальных посылок Т = 2Р элементов. Структура такого сигнала показана на рис.4.17.

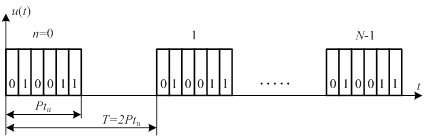
Рис. 4.17.

Значения корреляционной функции вычисляются по формуле:

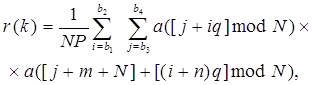(4.8)

где индексы элементов в скобках a(i) = a_i, n – дискретный сдвиг последовательностей, равный целому числу периодов повторения Т сигнальных посылок (0 ≤ n ≤ N –1), m – дискретный сдвиг последовательностей, равный числу элементов, на которое сдвинуты сигналы внутри периода, – (P –1) ≤ m ≤ (P –1), значок modN – суммирование по модулю N, q – циклический сдвиг ( сдвиг на q элементов вправо или влево) кодирующей последовательности в каждой последующей сигнальной посылке пачки 0 ≤ q ≤ N –1. Пределы суммирования определяются следующими соотношениями: b₁ = 0, b₂ = N –1 – n, b₃ = max(0, – m), b₄ = min(P –1, P –1– m).

Заметим, что при q = 0 все сигнальные посылки пачки кодируются одним и тем же периодом ПМП. Для q = 1 все сигнальные посылки пачки кодируются ПМП, сдвинутыми относительно друг друга на один элемент. Как показывают расчеты, уровень боковых выбросов корреляционной функции на интервале задержек –N ≤ k ≤ N не превышает значения 1/N, которое характерно для боковых выбросов непрерывной ПМП.