Общие сведения о статически неопределимых арках

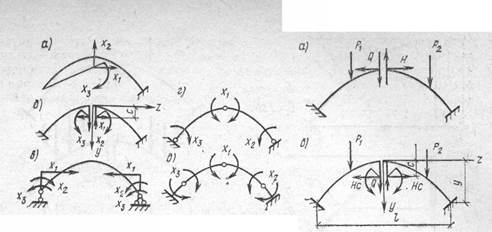
Статически неопределимые арки бывают двухшарнирные (рис. 3, а), бесшарнирные (рис. 3, 6) и редко применяемые одношарнирные (рис. 3, в). Арки могут быть симметричные и несимметричные. Двухшарнирные арки однажды, одношарнирные дважды и бесшарнир­ные трижды статически неопределимы. Замкнутые кривые стержни (кольца), если в них нет шарниров, также трижды статически неопре­делимы.

Ось кривого стержня и его поперечные сечения определяют форму арки, которая назначается на основании различных соображений. Главное соображение состоит в том, чтобы арка была рациональной. Теоретически рациональной формой арки данного типа при заданных значениях нагрузки, длины пролета и стрелы подъема арки считают такую, которая обеспечивает необходимую прочность и устойчивость арки при наименьшем ее объеме.

Ось рациональной арки и ее сечения определяются специальными исследованиями. Распределение материала по длине такой арки соот­ветствует распределению в ней внутренних сил.

Распределение материала по длине арки с заданной осью также должно соответствовать распределению внутренних сил и прежде всего изгибающих моментов и продольных сил. Примерное распределение на­ибольших по абсолютной величине изгибающих моментов от некоторой подвижной нагрузки по длине различных арок показано на рис. 4.

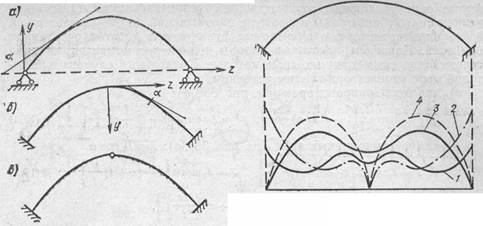Рис. 4

Рис. 3

Второе соображение при выборе формы арок основано на желании получить результаты расчета в виде простых формул. В соответствии с этим законы изменения площадей и моментов инерции поперечных сечений необходимо назначать исходя из двух условий:

1) размеры и форма сечений должны соответствовать распределению расчетных внут­ренних сил;

2) интегралы в формуле перемещений должны выражаться в конечном виде через элементарные функции при простых очертаниях оси арки.

Приведем некоторые законы изменения моментов инерции сечений для симметричных арок, которые в отдельных случаях в неко­торой мере удовлетворяют этим условиям:

а) для бесшарнирных арок (см. рис. 3, б) :

J = I₀ : cosα 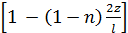; J = I₀ : cosα .

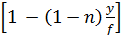б) для двухшарнирных арок (см. рис. 3, а): J = I₀ × cosα,

J = I₀ : cosα 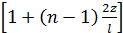; J = I₀ : cosα ;

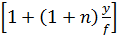J = I₀ : cosα ,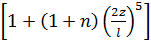

где n = J₀ : J_nсos α_n;

J_о — момент инерции в замке арки;

J_п — момент инерции в пяте арки.

При проектировании мостов, особенно городских, выбор формы арок определяется также архитектурными соображениями.

ЗАМЕЧАНИЕ К РАСЧЕТУ АРОК

Поскольку арка есть кривой стержень, то при точном ее расчете надо учитывать кривизну.

Заметим, однако, что применяемые в строительстве арки и своды, хотя иногда и могут иметь большую кривизну, как, например, трубы малых пролетов под большими насыпями, но они как правило, являются арками малой кривизны, для которых 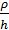>10. Для таких арок сложный учет кривизны в формуле перемещений часто дает малосущественные поправки, поэтому их расчет при ручном счете обычно приводится по формулам для стержня малой кривизны, что при использовании ЭВМ уже теряет смысл.

Влияние внутренних сил N и Q на перемещения в арках по сравнению с изгибающими моментами М, как правило, больше, чем в рамах Оно зависит от нагрузки и может быть оценено только по результатам расчета. При прочих равных условиях влияние N и Q для бесшарнирных арок обычно больше, чем для двухшарнирных . Если изгибающие моменты М в арке велики, влияние N и Q по сравнению с влиянием М уменьшается, и наоборот. В случаях когда арка имеет очертание по кривой давления для трехшарнирной арки, влияние М и Q относительно мало. При очертаниях арки, близких к кривой давления для трехшарнирной арки, особенно в пологих арках, преимущественное влияние на перемещения или, по крайней мере, равное влиянию изгибающего момента оказывает продольная сила N.

Существующее суждение о преимущественном во всех случаях влиянии N по сравнению с Q не всегда даже для относительно пологих арок правильно. В этом случае нельзя забывать о коэффициенте μ > 1 (для двутавровых сечений μ = 2,5—3) и модуле упругости G 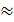0,4Е, которые увеличивают слагаемое в формуле перемещений, учитывающее влияние Q.

Поскольку арка во многих случаях представляет собой основную часть дорогого и ответственного сооружения, то не следует игнорировать без анализа влияние отдельных слагаемых при определении перемещений. Все принципиальные вопросы расчета арок могут быть изложены на основе более простой

формулы перемещений стержня малой кривизны.

ОСНОВНЫЕ СИСТЕМЫ ДЛЯ БЕСШАРНИРНЫХ АРОК

Рис. 5 Рис. 6

Основные системы для симметричных бесшарнирных арок разделя­ются на балочные (рис. 5, а—в) и арочные (рис. 5, г, д). Все ос­новные системы допускают расчленение канонических уравнений и при­ведение их к виду:

δ₁₁ Х₁ + Δ_1Р = 0; δ₂₂ Х₂ + Δ_2р = 0; δ₃₃ Х₃ + Δ_зр = 0.

В основных балочных системах а и б это достигается переносом сил в упругий центр, в системе в — переносом сил на уровень упругого цен­тра и группировкой неизвестных, а в основных арочных системах г и д — группировкой неизвестных.

Основная система а несимметричная, а потому неудобная. Система б симметричная, а значит удобная. Внутренние силы в этой системе от нагрузки определяются просто и во многих случаях на части основной системы они равны нулю. Система в также симметричная, но в ней при любой несамоуравновешенной нагрузке внутренние силы по всей ее длине не равны нулю. Арочные системы симметричны. В них внутрен­ние силы определяются сложнее, чем в балочных системах, и также, как правило, они не равны нулю по всей длине системы.

Внутренние силы от нагрузки в основных балочных системах значи­тельно отличаются от внутренних сил в бесшарнирной арке, а в ароч­ных системах продольные силы, например, близки продольным силам в арке, поэтому основные арочные системы (особенно д) ближе по своей работе к бесшарнирной арке, чем балочные.

Внутренние силы от нагрузки в бесшарнирной арке при использова­нии балочных основных систем вычисляются обычно как разность боль­ших близких чисел, что требует точных вычислений, а при использова­нии арочных систем они вычисляются как дополнительные слагаемые к внутренним силам трехшарнирных арок и могут быть вычислены с меньшей точностью.