Теоремы сложения и умножения вероятностей.
Теорема сложения вероятностей двух несовместных событий:
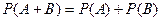(1).
В этой формуле: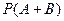 
- вероятность суммы двух несовместных событий 
и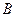 
, т. е. вероятность наступления одного из двух событий, безразлично какого (или , или );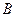 
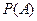- вероятность наступления события ; 
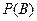- вероятность наступления события ; 
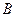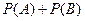- сумма вероятностей и .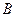
Если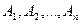 
- n попарно несовместных событий, то
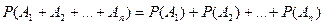(2).
Если 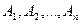образуют группу, то
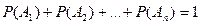. (3). Сумма двух совместных событий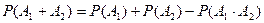 
Если и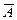 
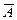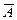- два несовместных события, образующих полную группу, то - событие противоположное событию . Вероятность события равна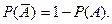 
Теорема умножения вероятностей:
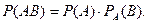(4)
В этой формуле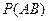 
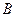- вероятность произведения двух зависимых событий и , т. е. вероятность их совместного наступления (наступления и события , и события 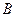); 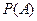- вероятность наступления события ; 
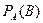- условная вероятность события 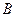, вычисленная в предположении, что событие уже наступило; 
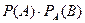- произведение вероятности события на условную вероятность .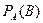
В частности, для двух независимых событий и :
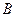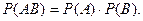(5)
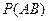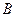В этой формуле - вероятность произведения двух независимых событий и , т. е. вероятность их совместного наступления (наступления и события , и события 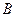), 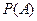- вероятность наступления события ; 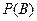- вероятность наступления события ; 
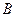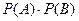- произведение вероятностей событий и .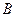
Если 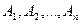- n зависимых событий, то
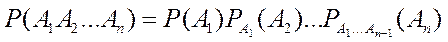(6).
В этой формуле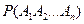 
- вероятность произведения событий 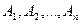, т. е. вероятность их совместного наступления; 
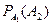- условная вероятность события 
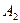, вычисленная в предположении, что событие 
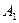наступило; …, 
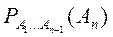- вероятность события 
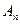, вычисленная в предположении, что все предыдущие 
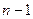события наступили.
В частности, для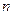 
независимых событий :
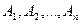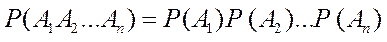, (7)
Где 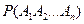- вероятность произведения событий ; 
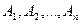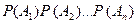- произведение вероятностей этих событий.
Задача образец 1.
В цехе работают семь мужчин и три женщины. По табельным номерам наудачу отобраны три человека. Найти вероятность того, что все отобранные лица окажутся мужчинами.
Решение.
Введем обозначение событий: - первым отобран мужчина; 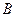- вторым отобран мужчина; С - третьим отобран мужчина. Вероятность того, что первым будет отобран мужчина 
.
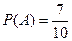Вероятность того, что вторым будет отобран мужчина, при условии, что первым уже был отобран мужчина, т. е. условная вероятность события 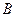следующая: 
.
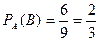Вероятность того, что третьим будет отобран мужчина, при условии, что уже отобраны двое мужчин, т. е. условная вероятность события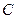 
такова: 
.
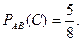Искомая вероятность того, что все три отобранных лица окажутся мужчинами,
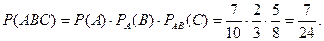
Задача образец 2.
В урне 4 белых, 6 черных, и 5 красных шаров. Из нее наугад вынимают один за другим два шара. Найти вероятность того, что оба шара одного цвета.
Решение.
Рассмотрим события:
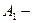первым извлечен белый шар;
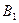- вторым извлечен белый шар;
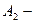первым извлечен черный шар;
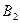- вторым извлечен черный шар;
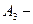первым извлечен красный шар;
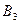- вторым извлечен красный шар;
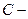извлечены два шара одного цвета.
Событие 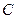представляет собой сумму следующих несовместных событий:
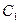- извлечены два белых шара;
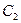- извлечены два черных шара;
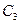- извлечены два красных шара;
Таким образом,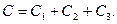 
Событие 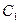заключается в том, что и первый, и второй, извлеченные из урны шара, являются белыми. Это означает, что событие 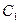представляет собой произведение событи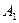й и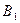 
: 
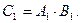Аналогично получим, что 
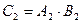и 
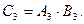
Вероятности событий 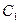, , 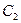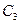найдем по теореме умножения вероятностей.
Событие 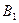является зависимым от события 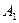, так как его вероятность изменяется при наступлении события 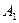. Используя классическое определение вероятности, получим, что вероятность события 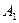равна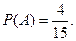 
Условная вероятность события 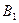, вычисленная при условии, что событие 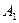произошло, равна 
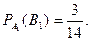Согласно формуле (4) получим:
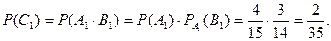
Рассуждая аналогично, найдем
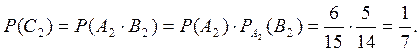
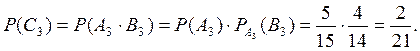
Вычислив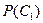 
, 
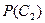и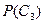 
, найдем искомую вероятность 
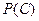по теореме сложения вероятностей несовместных событий:
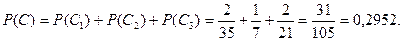
Далее самостоятельно.
Задача 1.
В денежной вещевой лотерее на каждые 1000 билетов приходится 5 денежных и 20 вещевых выигрышей. Какова вероятность выигрыша на один билет?
Ответ: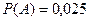 
. Указание: использовать формулу сложения вероятностей.
Задача 2.
Контрольная работа по математике оценивается целым числом баллов, причем наибольшее число баллов равно 10. Вероятность получить студенту N за эту работу 10 баллов равна 0,2; 9 баллов – 0,3 и от 1 до 9 включительно – 0,7. найти вероятность того, что студент N получит: а) не менее 9 баллов, б) ноль баллов.
Ответ: а)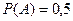 
, б)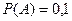 
Указание: использовать формулу сложения вероятностей (1).
Задача 3.
В читальном зале имеется шесть учебников по теории вероятностей, из которых три в переплете. Библиотекарь наудачу взял два учебника. Найти вероятность того, что оба учебника окажутся в переплете.
Ответ: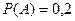 
. Указание: использовать формулу умножения вероятностей (4).
Задача 4.
В круг радиуса R вписан равносторонний треугольник. Какова вероятность того, что четыре наугад поставленные в данном круге точки окажутся внутри треугольника?
Ответ: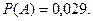 
Задача 5.
Партия из ста деталей подвергается выборочному контролю. Условием непригодности всей партии является наличие хотя бы одной дефектной детали среди четырех проверяемых. Какова вероятность того, данная партия не будет принята, если она содержит 3 % дефектных деталей?
Ответ: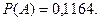 
Указание использовать формулу (6).
Задача 6.
Сколько нужно выбрать чисел из таблицы случайных чисел, чтобы с вероятностью, не меньшей 0,9 быть уверенным в том, что среди них хотя бы одно число четное?
Ответ: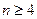 
Указание использовать формулу (7).
Задача 7.
Студент знает 20 и 25 вопросов программы. Найти вероятность того, что студент знает переложенные ему три вопроса.
Ответ: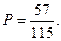 
Задача 8.
Случайно смешаны кусты рассады двух сортов томатов: 9 кустов рассады сорта Белый налив и 7 – сорта Верлиока. Найти вероятность того, что первые три, посаженные друг за другом куста томатов, являются рассадой сорта Белый налив.
Ответ: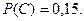 
Тема 5.