Аналитическая геометрия в пространстве

1. Уравнение поверхности. Рассмотрим в пространстве некоторую поверхность. Пусть точка М(x, y, z) движется по поверхности. Координаты ее меняются, но они меняются не произвольно, они удовлетворяют некоторому условию, которое удерживает точку М на поверхности. Это условие записывается как уравнение между координатами точки М(x, y, z).

F(x, y, z) = 0.

Этому уравнению удовлетворяют координаты любой точки, лежащей на поверхности, и не удовлетворяют координаты точек, не лежащих на поверхности.

П р и м е р . Найти уравнение сферы с центром в точке О₁ (a, b, c) и радиусом R.

M(x,y, z) – произвольная точка сферы.

О₁М = R, ,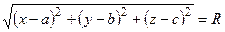

(x – a)² + (y – b)² + (z – c)² = R² – уравнение сферы.

1. Уравнение линии в пространстве.

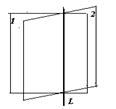
Линия в пространстве задается как пересечение двух поверхностей (1) и (2).

F₁(x, y, z) = 0, (1)

F₂(x, y, z) = 0. (2)

Если точка принадлежит линии (L), то она одновременно принадлежит поверхности (1) и поверхности (2). Координаты ее при этом удовлетворяют системе уравнений (1) и (2).

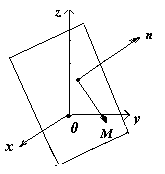
3. Уравнение плоскости. Пусть положение плоскости в пространстве определяется заданием точкиМ₀(x₀, y₀, z₀) и нормального вектора n = {A, B, C}. Составим уравнение плоскости. Пусть точка М(x, y, z,) – произвольная точка плоскости.

М₀М= {x – x₀, y – y₀, z – z₀}.

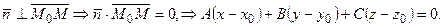- (1)

уравнение плоскости, проходящей через данную точку. Это уравнение преобразуется к виду Ах + By + Cz + D = 0 (2)

т.е. является линейным относительно x, y и z. Докажем, что всякое линейное уравнение определяет плоскость. Пусть (x₀, y₀, z₀) – решение уравнения (2) . Тогда

Ax₀ + By₀ +Cz₀ + D = 0 (3)

Из уравнения (2) вычтем уравнение (3).

A(x – x₀) + B(y – y₀ ) + C(z – z₀) = 0 – уравнение плоскости.

Следовательно, уравнение (2) определяет плоскость. А, В, С – координаты нормального вектора этой плоскости.
(1) A₁x + B₁y + C₁z + D₁ = 0, n₁ = {A₁, B₁, C₁}

(2) A₂x + B₂ y + C₂z + D₂ = 0. n₂ = {A₂, B₂, C₂}

a) n₁ ║ n₂ 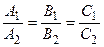- условие параллельности плоскостей.

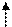
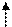
n₁ b) -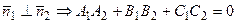

условие перпендикулярности плоскостей

n₂

n₁

n₂

с)Даны три точки, лежащие на плоскости M₁(x₁, y₁, z₁), M₂(x₂, y₂, z₂), M₃(x₃, y₃, z₃). Возьмем

на плоскости произвольную точку М(x, y, z). Векторы М₁М, М₁М₂, М₁М₃ компланарны.

М₁ М 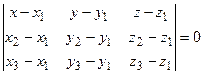- уравнение плоскости.

М₂

М₃ проходящей через три точки.

П р и м е р . Написать уравнение плоскости, проходящей через точку (2, 0, 3) параллельно плоскости 3x + 4y - 2z + 5 = 0.

3(x – 2) + 4(y – 0) – 2(z – 3) = 0.

1. Прямая линия в пространстве. Прямая в пространстве задается как линия пересечения двух плоскостей.

A₁x + B₁y + C₁z + D₁ = 0, общие уравнения прямой.

A₂x + B₂ y + C₂z + D₂ = 0.

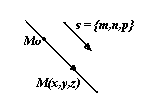Пусть на прямой известна точка М₀(x₀, y₀, z₀) и направляющий вектор s = {m, n, p} – любой вектор, параллельный прямой. M(x, y, z) – произвольная точка, лежащая на прямой. Тогда

M₀M ║ s, M₀M = {x – x₀, y – y₀, z – z₀ }

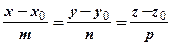- канонические уравнения прямой.

Очевидно, если имеем две прямые с направляющими векторами s₁ ={m₁, n₁, p₁} и
s₂ = {m₂, n₂ , p₂}, то 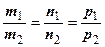- условие параллельности двух прямых,
m₁m₂ + n₁n₂ + p₁p₂ = 0 – условие перпендикулярности двух прямых.

1. Прямая и плоскость. Рассмотрим плоскость Ax + By + Cz + D = 0, n ={A, B, C},

и прямую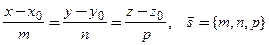

s={m, n, p}Am + Bn + Cp = 0 – условие параллельности прямой и

n = {A, B, C} и плоскости

n = {A, B, C}

s = {m, n, p} 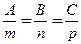условие перпендикулярности прямой и плоскости.

З а д а ч и.

1. Написать уравнение прямой, проходящей через точку (2, 1, 3), параллельно прямой

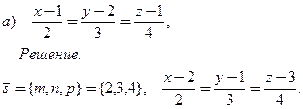
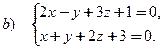
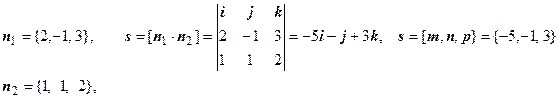
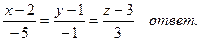
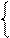1. Написать уравнение плоскости, проходящей через точку М₀(0, 1, -2) перпендикулярно прямой 2 x – y + 3z + 1 = 0,

x + y + 2z + 3 = 0.

Решение. A(x – x₀) + B(y – y₀) + C(z – z₀) = 0. n = {A, B, C,} = {-5, -1, 3}.

-5(x – 0) -1(y – 1) + 3(z + 2) = 0. 5x + y – 3z - 7 = 0 – ответ.

3. Даны координаты вершин пирамиды ABCD: А(3, 1, 4), В(-1, 6, 1), C(-1, 1, 6),
D(0, 4, -1). Найти

длину ребра АВ;

угол между ребрами АВ и AD;

площадь грани АВС;

объем пирамиды;

уравнение прямой АВ;

уравнение плоскости АВС;

уравнение высоты, опущенной из вершины D на грань АВС.

D AB ={-4, 5, -3},

AD= {-3, 3, -5}

AC = {-4, 0, 2}

n

A B

O₁

C

Решение.

3.1.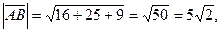

3.2. 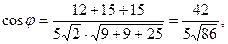3.3. n =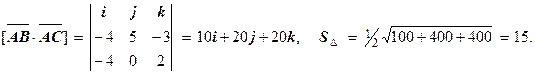

3.4.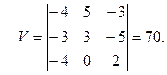

3.5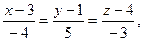

3.6. n = {10, 20, 20}, 10(x - 3) + 20(y – 1) + 20(z – 4) = 0, x + 2y + 2z - 13 = 0.

3.7. s = n = {10, 20, 20},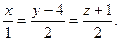

Цилиндрические поверхности.

z

M (x,y,z)

(A)

y

M₁(x, y) (L)

x

Пусть прямая (A) движется вдоль кривой (L), оставаясь параллельной своему первоначальному положению. Поверхность, которая при этом получается, называется цилиндрической. Рассмотрим уравнение

F(x, y) = 0. (1)

В плоскости (x, y) оно определяет линию (L). Если уравнению (1) удовлетворяют координаты точки М₁(х, y), то ему удовлетворяют и координаты любой точки М(x, y, z) прямой, параллельной оси z.

F(x, y) = 0 – уравнение цилиндрической поверхности с образующими, параллельными оси z.

Аналогично, F(x, z) = 0 – цилиндрическая поверхность с образующими, параллельными оси y. F(y, z) = 0 – цилиндрическая поверхность с образующими, параллельными оси x.

Например, y² = 2x – параболический цилиндр, с образующими, параллельными оси z.

z

y

x