Требования к оформлению контрольной работы 1 страница

Физика

Часть I

Физические основы механики. Элементы специальной теории относительности. Механические колебания и волны. Основы термодинамики. Электростатика и постоянный ток.

Методическое пособие

для студентов всех технических специальностей

заочного отделения

Вологда

УДК

Физика: Методическое пособие для студентов всех технических специальностей заочного отделения. – Вологда: ВоГТУ, 2009 - 139 с.

Утверждено редакционно-издательским советом ВоГТУ.

Составители:

Богданов, В.И., профессор, доктор физ.-мат. наук

Корнейчук, С.К., доцент, канд. физ.-мат. наук

Попов В.А., старший преподаватель

Штрекерт О.Ю., канд. физ.-мат. наук, доцент

Содержание

Введение 4

Программа учебного курса (часть первая) 4

Физические основы механики

Элементы специальной теории относительности

Механические колебания и волны 8

Контрольная работа № 1 48

Гидродинамика

Основы термодинамики 56

Контрольная работа № 2 73

Электростатика

Постоянный ток 81

Контрольная работа № 3 120

Приложения 130

Библиографический список 139

Введение

Курс общей физики студенты заочного отделения изучают на втором и третьем курсах. Занятия по расписанию проводятся в форме лекций, практических и лабораторных занятий, а также в виде консультаций.

Контроль знаний осуществляется при защите контрольных работ, в виде отчетов за проделанные лабораторные работы, а также в виде зачетов и экзаменов. Содержание курса изложено в рабочей программе. Рабочая программа курса составлена на основе требований Государственного стандарта для рассматриваемых специальностей. В программе даны: тематика лекций, темы практических занятий, список лабораторных работ.

Программа учебного курса (часть первая)

Цель курса:раскрыть содержание основных законов и понятий физики; обеспечить понимание и усвоение физических закономерностей и явлений, которые необходимы для изучения общетехнических и специальных дисциплин.

Содержание курса

Тема 1:Физические основы механики. Элементы специальной теории относительности

1.1. Кинематика поступательного и вращательного движения материальной точки.

1.2. Динамика материальной точки. Силы в природе. Закон Всемирного тяготения. Системы отсчета в механике.

1.3. Импульс. Закон сохранения импульса. Энергия как количественная мера движения материи. Работа силы. Мощность. Кинетическая энергия и ее связь с работой. Потенциальная энергия. Закон сохранения энергии для системы материальных точек.

1.4. Динамика абсолютно твердого тела: момент инерции и момент импульса. Уравнение моментов. Закон сохранения момента импульса для системы материальных точек. Момент инерции твердого тела относительно неподвижной оси вращения. Основное уравнение динамики вращательного движения. Теорема Штейнера. Кинетическая энергия твердого тела.

1.5. Механика сплошных сред: давление, закон Паскаля, закон Архимеда. Равновесие, погруженных в жидкость, тел. Идеальная жидкость. Уравнение неразрывности струи. Уравнение Бернулли. Течение вязкой жидкости. Ламинарное и турбулентное течение. Число Рейнольдса. Движение вязкой жидкости в трубе. Формула Пуазейля. Метод Стокса. Движение тел в жидкостях и газах.

1.6. Постулаты Эйнштейна. Преобразования Лоренца. Инварианты преобразований. Элементы релятивистской динамики: масса, импульс и энергия.

Тема 2:Механические колебания и волны

3.1. Понятие о колебательных процессах. Смещение, скорость, ускорение материальной точки, совершающей колебательное движение. Амплитуда. Период. Частота. Сложение гармонических колебаний. Маятники: физический, математический и пружинный. Свободные колебания. Коэффициент затухания, декремент затухания, добротность колебательной системы.

3.2. Понятие волны. Продольные и поперечные волны. Волновое уравнение. Энергия бегущей волны. Вектор Умова.

Тема 3: Основы термодинамики

4.1. Термодинамический метод. Макроскопические параметры. Уравнение состояния. Первое начало термодинамики. Классическая теория теплоемкости идеального газа. Адиабатный процесс.

4.2. Обратимые и необратимые тепловые процессы. Тепловые двигатели. Второе начало термодинамики в формулировке Томпсона и Клаузиуса. Цикл Карно. КПД тепловой машины. Энтропия. Закон возрастания энтропии. Цикл Карно в (T,S) – координатах.

4.3. Фазовые переходы первого рода. Условия равновесия фаз. Диаграмма фазового равновесия. Тройная точка. Фазовые переходы второго рода. Λ-переходы.

Тема 4: Электростатика и постоянный ток

4.1. Электростатическое поле в вакууме: закон сохранения электрического заряда. Закон Кулона. Напряженность поля. Теорема Остроградского – Гаусса для электростатического поля в вакууме. Работа сил поля. Потенциал. Связь потенциала с напряженностью поля.

4.2. Электрическое поле в диэлектриках: поляризация диэлектрика, поляризованность, виды поляризации в диэлектриках. Сегнетоэлектрики. Гистерезис. Петля гистерезиса. Вектор электростатической индукции. Относительная диэлектрическая проницаемость и диэлектрическая восприимчивость.

4.3. Проводники в электрическом поле.Связь напряженности поля у поверхности проводника с поверхностной плотностью заряда. Конденсаторы. Электроемкость. Энергия электрического поля в конденсаторе.

4.4. Постоянный электрический ток и его характеристики: сила тока, плотность тока. Удельная проводимость и удельное сопротивление проводника. Сверхпроводимость. Закон Ома и закон Джоуля – Ленца в дифференциальной форме записи. Сторонние силы и электродвижущая сила. Закон Ома для полной цепи. Законы Кирхгофа. Классическая теория электропроводности металлов.

Контрольные работы

Контрольные работы позволяют закрепить теоретический материал. В процессе изучения первой части курса физики студент должен выполнить три контрольные работы. Решение задач является проверкой степени усвоения студентами теоретического курса, а рецензии на работу помогают ему доработать и правильно усвоить различные разделы курса физики. Контрольные работы выполняются в период между сессиями и отдаются на кафедру физики для проверки не позднее, чем за 15 дней до начала сессии.

Перед выполнением контрольной работы необходимо внимательно ознакомиться с примерами решения задач по данной теме, уравнениями и формулами, а также со справочными материалами. Прежде, чем приступить к решению той или иной задачи, необходимо разобраться в ее содержании и поставленных вопросах.

Контрольные работы для инженерно-технических специальностей, включенных в данное пособие, распределены следующим образом:

№ 1 – Физические основы механики. Элементы специальной теории относительности. Механические колебания и волны.

№ 2 – гидродинамика, основы термодинамики;

№ 3 –электростатика и постоянный ток.

Каждая контрольная работа содержит 8 задач. Номер варианта контрольной работы выбирается студентом по последней цифре в зачетной книжке. Таблица вариантов представлена после примеров задач по каждой рассмотренной теме.

Решенные задачи следует оформить так, как указано ниже.

Контрольные работы, оформленные без соблюдения правил, а также работы, выполненные не по своему варианту, зачтены не будут.

При наличии значительных ошибок и неправильных решений работа возвращается студенту для исправлений. После исправления работа отправляется на кафедру физики на повторное рецензирование. Защита контрольных работ происходит в виде собеседования по решенным задачам на консультациях во время сессии.

Требования к оформлению контрольной работы

1. Контрольная работа оформляется в отдельной тетради. Титульный лист оформляется следующим образом:

Контрольная работа по физике №…

“Название к.р.”

Студент ----------- группы ----------

......................................Шифр………..

Фамилия, Имя, Отчество

Вариант №…………………..

Проверил……………………………

Фамилия, Имя, Отчество преподавателя

“Зачтено”дата…………….роспись……….

2. Каждая задача оформляется с начала нового листа. Записывается полностью текст задачи так, как он приведен в методичке.

3. Все, содержащиеся в задаче данные, которые могут быть представлены в виде математических соотношений, должны быть записаны в колонке под заголовком “Дано”.

4. Величины, выраженные через внесистемные единицы, должны быть выражены через единицы системы СИ. Численное значение всех величин должно быть представлено в нормализованном виде: (1÷10)10ⁿ

5. Решению задачи должно предшествовать изображение физических явлений и процессов, происходящих в данной задаче. На рисунке, чертеже или блок-схеме должны быть указаны характерные параметры данной задачи, известные и искомые величины.

6. Задачу рекомендуется решить сначала в общем виде, т.е. только в буквенных обозначениях, поясняя при написании формул буквенные обозначения. Решение задачи должно содержать краткие пояснения основных этапов. Значение фундаментальных физических констант должно быть приведено с указанием численного значения размерности в системе СИ.

7. Далее необходимо провести проверку размерности полученного выражения. Для этого в конечную формулу для искомой величины необходимо подставить вместо буквенных параметров их размерности в системе СИ. Затем преобразовать эти размерности, используя связи и соотношения между самими величинами в виде физических законов и определяющих формул. Полученная в результате проверки размерность искомой величины должна совпадать с ее размерностью в системе СИ.

8. После проверки размерности в полученную формулу для искомой величины подставить численные значения каждого из параметров задачи и записать ответ.

9. Полученное значение искомой величины должно быть проанализировано с точки зрения вероятности ее попадания в интервал возможных значений.

Данный перечень требований должен быть применен к каждой из задач!

10. В конце контрольной работы, после решения всех указанных в маршруте задач, необходимо привести список использованной литературы.

Контрольные работы, оформленные без соблюдения правил, а также работы, выполненные не по своему варианту, зачтены не будут.

МЕХАНИКА

основные формулы

КИНЕМАТИКА

• Положение материальной точки в пространстве задается радиусом-вектором: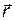

где — единичные векторы направлений (орты); — координаты точки.

Кинематические уравнения движения в координатной форме:

где t — время.

• Средняя скорость:

.

где 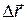— перемещение материальной точки за интервал времени .

• Средняя путевая скорость:

где — путь, пройденный точкой за интервал времени .

• Мгновенная скорость:

где — проекции скорости на оси координат.

Модуль скорости:

.

• Ускорение:

,

где: - проекции ускорения 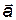на оси координат.

Модуль ускорения: .

При криволинейном движении ускорение можно представить как сумму нормальной 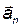и тангенциальной 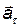составляющих:

.

Модули этих ускорений:

; ; ,

где R — радиус кривизны в данной точке траектории.

• Кинематическое уравнение равномерного движения материальной точки вдоль оси х:

,

где — начальная координата; t — время. При равномерном движении

и .

• Кинематическое уравнение равнопеременного движения ( ) вдоль оси x:

,

где v₀ ‑ начальная скорость; t ‑ время.

Скорость точки при равнопеременном движении:

.

• Положение твердого тела (при заданной оси вращения) определяется углом поворота (или угловым перемещением) .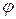

Кинематическое уравнение вращательного движения:

.

• Средняя угловая скорость:

,

где — изменение угла поворота за интервал времени . Мгновенная угловая скорость:

.

• Угловое ускорение:

.

• Кинематическое уравнение равномерного вращения:

,

где - начальное угловое перемещение; t - время. При равномерном вращении и .

Угловая скорость и угловое ускорение являются аксиальными векторами, их направления совпадают с осью вращения.

• Частота вращения:

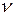=N/t, или 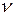=1/T,

где N — число оборотов, совершаемых телом за время t; Т — период вращения (время одного полного оборота).

• Кинематическое уравнение равнопеременного вращения ( .)

,

где 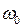- начальная угловая скорость; t - время.

Угловая скорость тела при равнопеременном вращении

.

• Связь между линейными и угловыми величинами, характеризующими вращение материальной точки, выражается следующими формулами:

путь, пройденный точкой по дуге окружности радиусом R,

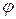( - угол поворота тела);

скорость точки линейная

; ;

ускорение точки:

тангенциальное

; ;

нормальное

; .

ДИНАМИКА МАТЕРИАЛЬНОЙ ТОЧКИ И ТЕЛА, ДВИЖУЩИХСЯ ПОСТУПАТЕЛЬНО

• Уравнение движения материальной точки (второй закон Ньютона):

в векторной форме:

, или ,

где — геометрическая сумма сил, действующих на материальную точку; т — масса; 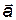— ускорение;— импульс; N — число сил, действующих на точку;

в координатной форме (скалярной):

, ,

или

, , ,

где под знаком суммы стоят проекции сил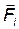 , на соответствующие оси координат.

Сила гравитационного взаимодействия:

,

где G — гравитационная постоянная; m₁ и m₂ — массы взаимодействующих тел, рассматриваемые как материальные точки; r — расстояние между ними.

Сила трения скольжения:

,

где — коэффициент трения скольжения; N — сила нормального давления.

• Сила упругости:

,

где k — коэффициент упругости (жесткость в случае пружины);

— абсолютная деформация.

• Координаты центра масс системы материальных точек:

, , ,

где m_i — масса i-й материальной точки; x_i, y_i;, z_i; — ее координаты.

• Закон сохранения импульса:

или ,

где N — число материальных точек (или тел), входящих в систему.

• Работа, совершаемая постоянной силой:

или ,

где 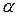— угол между направлениями векторов силы 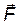и перемещения .

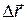• Работа, совершаемая переменной силой:

,

где интегрирование ведется вдоль траектории, обозначаемой L.

• Средняя мощность за интервал времени :

.

• Мгновенная мощность:

или ,

где — работа, совершаемая за промежуток времени dt.

• Кинетическая энергия материальной точки (или тела), движущейся поступательно:

или .

• Потенциальная энергия тела и сила, действующая на тело в данной точке поля, связаны соотношением

или ,

где— единичные векторы (орты). В частном случае, когда поле сил обладает сферической симметрией (как, например, гравитационное),

.

• Потенциальная энергия упругодеформированного тела (сжатой или растянутой пружины)

.

• Потенциальная энергия гравитационного взаимодействия двух материальных точек (или тел) массами m₁, и т₂, находящихся на расстоянии r друг от друга:

.

• Потенциальная энергия тела, находящегося в однородном поле силы тяжести,

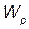=mgh,

где h — высота тела над уровнем, принятым за нулевой для отсчета потенциальной энергии. Эта формула справедлива при условии , где R — радиус Земли.

• Закон сохранения энергии в механике выполняется в замкнутой системе, в которой действуют только консервативные силы, и записывается в виде:

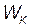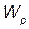+ =const.

ДИНАМИКА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ОСИ

• Момент силы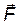 , действующей на тело, относительно оси вращения:

,

где — проекция силы 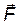на плоскость, перпендикулярную оси вращения; l — плечо силы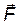(кратчайшее расстояние от оси вращения до линии действия силы).

• Момент инерции относительно оси вращения:

а) материальной точки

,

где т — масса точки; r — расстояние ее от оси вращения;

б) дискретного твердого тела

,

где — масса i-го элемента тела; r_i — расстояние этого элемента от оси вращения; N — число элементов тела;

в) сплошного твердого тела

.

Если тело однородно, т. е. его плотность одинакова по всему объему, то

и ,

где V — объем тела.

• Моменты инерции некоторых тел правильной геометрической формы:

Тело	Ось, относительно которой определяется момент инерции	Формула момента инерции
Однородный тонкий стержень массой т и длиной l	Проходит через центр тяжести стержня перпендикулярно стержню
Проходит через конец стержня перпендикулярно стержню
Тонкое кольцо, обруч, труба радиусом R и массой т, маховик радиусом R и массой т, распределенной по ободу	Проходит через центр перпендикулярно плоскости основания
Круглый однородный диск (цилиндр) радиусом R и массой т	Проходит через центр диска перпендикулярно плоскости основания
Однородный шар массой т и радиусом R	Проходит через центр шара

• Теорема Штейнера. Момент инерции тела относительно произвольной оси: