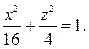Задания для контрольной работы.
1. На плоскости даны два вектора 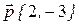 и
и 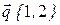 . Найти разложение вектора
. Найти разложение вектора 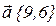 по базису
по базису 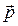 и
и 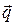 .
.
2. Даны три вектора 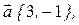
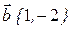 и
и 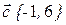 . Найти разложение вектора
. Найти разложение вектора 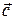 по базису
по базису 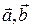 .
.
3. Даны три вектора 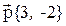 ,
, 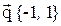 . Найти разложение вектора
. Найти разложение вектора 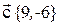 по базису
по базису 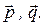
4. Даны четыре вектора: 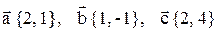 . Найти разложение вектора
. Найти разложение вектора 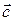 по векторам
по векторам 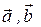 .
.
5. Векторы 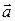 и
и 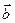 образуют угол
образуют угол 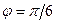 ; зная, что
; зная, что 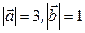 , найти скалярное произведение векторов
, найти скалярное произведение векторов 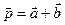 и
и 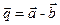 .
.
6. Найти скалярное произведение векторов 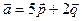 и
и 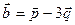 , если
, если 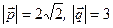 и
и 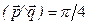 .
.
7. Известно, что | 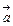 |=3, |
|=3, | 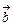 |= 4;
|= 4; 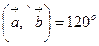 . Вычислить: скалярное произведение векторов
. Вычислить: скалярное произведение векторов 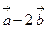 и
и 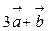 .
.
8. Векторы 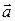 и
и 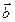 образуют угол
образуют угол 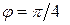 ; зная, что
; зная, что 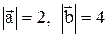 , найти скалярное произведение векторов
, найти скалярное произведение векторов 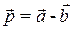 и
и 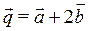 .
.
9. Даны вершины треугольника А(2, –5), В(1, –2), С(4, 7). Вычислить координаты центра тяжести этого треугольника. Найти длину медианы АМ.
10. Даны вершины треугольника А(–1, –1), В(3, 5), С(–4, 1). Вычислить координаты центра тяжести этого треугольника. Найти длину медианы ВМ.
11. Даны вершины треугольника А(1, 4), В(3, –9), С(–5, 2). Вычислить координаты центра тяжести этого треугольника. Найти длину медианы АМ.
12. Даны вершины треугольника А(3, –1), В(1, 1), С(2, 3). Вычислить координаты центра тяжести этого треугольника. Найти длину медианы ВМ.
13. Точка 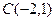 делит отрезок АВ в отношении
делит отрезок АВ в отношении 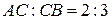 . Найти координаты точки В, если
. Найти координаты точки В, если 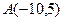 .
.
14. Точка 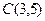 делит отрезок АВ в отношении
делит отрезок АВ в отношении 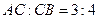 . Найти координаты точки А, если
. Найти координаты точки А, если 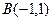 .
.
15. Отрезок АВ двумя точками разделен на три равные части. Определить координаты точек деления, если 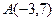 ,
, 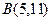 .
.
16. Точка 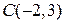 делит отрезок АВ в отношении
делит отрезок АВ в отношении 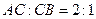 . Найти координаты точки В, если
. Найти координаты точки В, если 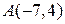 .
.
17. Составить уравнение эллипса, фокусы которого лежат на оси абсцисс симметрично относительно начала координат, если его малая ось равна 6, а расстояние между директрисами равно 13.
18. Составить уравнение эллипса, фокусы которого лежат на оси ординат симметрично относительно начала координат, если расстояние между фокусами 24, а эксцентриситет равен 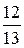 .
.
19. Составить уравнение гиперболы, фокусы которой расположены на оси абсцисс симметрично относительно начала координат, если она имеет асимптоты 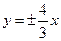 и расстояние между фокусами равно 20.
и расстояние между фокусами равно 20.
20. Составить уравнение гиперболы, фокусы которой расположены на оси абсцисс симметрично относительно начала координат, если расстояние между директрисами равно 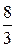 и эксцентриситет равен
и эксцентриситет равен 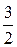 .
.
21. Составить уравнение параболы, вершина которой находится в начале координат, парабола симметрична относительно оси Ох и проходит через точку А(1, 3).
22. Составить уравнение параболы, вершина которой находится в начале координат, парабола симметрична относительно оси Ох и проходит через точку А(–4, 2).
23. Составить уравнение параболы, вершина которой находится в начале координат, парабола симметрична относительно оси Оу и проходит через точку А(3, –5).
24. Составить уравнение параболы, вершина которой находится в начале координат, парабола симметрична относительно оси Оу и проходит через точку А(–2, 1).
25. Даны вершины треугольника АВС А(1;1;-2), В(1;1;0), С(-1;3;0). Вычислить длину его высоты АН. (Используя векторное произведение векторов)
26. Дан треугольник АВС, в котором А(-1;1;2), В(1;1;0), С(2;6;-2). Вычислить длину его высоты ВН. (Используя векторное произведение векторов)
27. Дан треугольник АВС, в котором А(-1;1;2), В(1;1;0), С(2;6;-2). Вычислить площадь треугольника АВС, длину высоты CH. (Используя векторное произведение векторов)
28. Дан треугольник АВС, в котором А(6;5;-1), В(12;1;0), С(1;4;-5). Вычислить площадь треугольника АВС, длину высоты CH. (Используя векторное произведение векторов)
29. Вычислить объем тетраэдра, вершины которого находятся в точках
А(2;-1;0), В(5;4;3), С(3;1;-1) и D(4;-1;3).
30. Даны вершины тетраэдра: А(-2;3;0), В(4;2;-1), С(5;3;6), D(-4;-5;9). Найти длину его высоты, опущенной из вершины Д.
31. Объём тетраэдра V=7, три его вершины находятся в точках А(-2;0;-1), В(3;-1;1), С(2;-1;4). Найти координаты четвертой вершины Д, если известно, что она лежит на оси Oу.
32. Даны вершины тетраэдра: А(7;5;-1), В(0;-2;1), С(2;-2;4), Д(-4;1;3). Найти длину его высоты, опущенной из вершины В.
33. Составить уравнение плоскости, которая проходит через точку с координатами М1(3;-2;-7) и параллельно плоскости 2x-3z+5=0.
34. Составить уравнение плоскости, которая проходит через начало координат перпендикулярно к двум плоскостям: 2x-y+3z-1=0, x+2y+z=0.
35. Составить уравнение плоскости, которая проходит через точку М1(2;-1;1) перпендикулярно к двум плоскостям: 2x-z+1=0, y=0.
36. Составить уравнение плоскости, которая проходит через две точки
М1(1;-1;-2) и М2(3;1;1) перпендикулярно к плоскости x-2y+3z-5=0.
37. Составить уравнения прямой, которая проходит через точку М1(-1;2;-3) параллельно прямой: 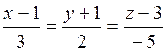 .
.
38. Составить уравнения прямой, которая проходит через точку М1(-4;-5;3) параллельно прямой: 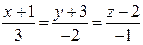
39. Составить уравнение прямой, которая проходит через точку М1(2;3;-5) параллельно прямой: x=3t-7, y=-2t+4, z=3t+4.
Составить каноническое уравнения прямой, которая проходит через точку М0(3;-2;-4) параллельно прямой 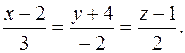
40. Вычислить кратчайшее расстояние между двумя прямыми в каждом из следующих случаев:
1) 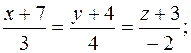
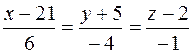
2) x=2t-4, y=-t+4, z=-2t-1;
x=4t-5, y=-3t+5, z=-5t+5
3) 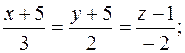

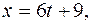 y=-2t, z=-t+2
y=-2t, z=-t+2
4) 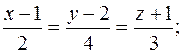
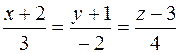
41. Даны вершины эллипсоида А1(8;0;0); А2(-2;0;0). Написать уравнение этого
эллипсоида, зная, что плоскость YOZ пересекает его по эллипсу: x=0, 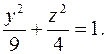
42. Оси симметрии однополостного гиперболоида Ф служат осями
ортонормированного репера и Ф проходит через эллипс 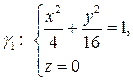 и
и
гиперболу 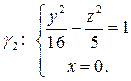 Написать уравнение гиперболоида Ф.
Написать уравнение гиперболоида Ф.
43. Оси симметрии однополостного гиперболоида служат осями ортонормированного репера. Написать уравнение этого гиперболоида, если он проходит через линию 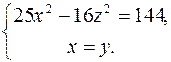 и точку М0(3;4;3).
и точку М0(3;4;3).
44. Написать уравнение эллипсоида, оси которого совпадают с осями координат и который проходит через точку М0(3;1;0) и пересекает плоскость хОz по эллипсу