Изучение явлений переноса коэффициента теплопроводности металла

Лабораторная работа № 2. 10.

Цель работы: изучение кинетических свойств твёрдых тел. Определение коэффициента теплопроводности металла.

Оборудование:печь, термопара, милливольтметр, регулятор.

I. Основные понятия и определения.

Распределение температуры Т вдоль нагреваемого с одного конца стержня, ось которого совпадает с осью х (рис.1), даётся решением дифференциального уравнения. Для того чтобы получить это уравнение рассмотрим отрезок стержня длиной dx.

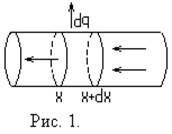
Количество тепла, проходящее через площaдь S поперечного сечения, соответствующее точке х определяется выражением:

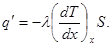
Количество тепла, проходящее через сечение, соответствующее точке х+dx, равно:

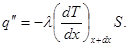
Через боковую поверхность отрезка длиной dx теряется количество тепла

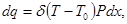(1)

Где 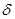– коэффициент теплоотдачи, P – периметр поперечного сечения, T₀ – температура окружающей среды. При стационарном процесс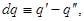е т.е.

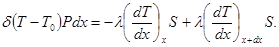
Разлагая это выражение в ряд и пренебрегая бесконечно малыми высших порядков, можем записать

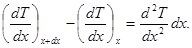
Откуда имеем:

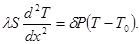(2)

Введём обозначение 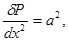тогда из (2) получим:

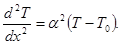(3)

Из решения этого уравнения можно получить выражение для коэффициента теплопроводности. Для этого полагая, что при х=0 температура Т= Т₁, а сам стержень бесконечно длинный, т.е. при x = ∞ и Т=Т₀ , получим:

Т – Т₀=(Т₁ –Т₀) е^-ах, (4)

откуда:

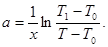(5)

Тогда количество теплоты, теряемое стержнем через боковую его поверхность (см. уравнение (1)), используя (4), может быть записано в виде:

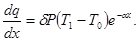(6)

Интегрируя это выражение в пределах от 0 до ∞, получим:

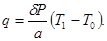(7)

Исключая коэффициент теплоотдачи 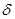, используя значение для а² (см. обозначение после формулы (2)), получаем окончательно:

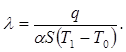(8)

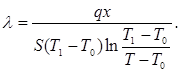или (9)

Для определения теплопроводности согласно этой формуле необходимо знать количество тепла q, отдаваемое стержнем при стационарном режиме через поверхность стержня, температуру нагреваемого конца стержня Т₁ , температуру Т в какой – либо точке стержня на расстоянии х от нагреваемого конца, площадь поперечного сечения S и температуру окружающей среды Т₀.

Практически, конечно, невозможно иметь бесконечно длинный стержень, однако, чем длиннее, тем точнее может быть измерена величина коэффициента теплопроводности. Найдём величину ошибки, полагая, что стержень имеет длину ℓ. Из уравнения (6), интегрируя его от х = ℓ до х = ∞, получим:

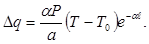
Разделив это соотношение на выражение (7), полученное путём интегрирования того же уравнения (6) в пределах от х = 0 до х = ∞, получим:

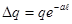. (10)

Это выражение даёт величину ошибки, допускаемой при определении теплоты q, когда принимают стержень длины ℓ за бесконечно длинный.

II. Методика эксперимента.

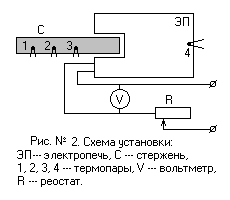
Для определения коэффициента теплопроводности в данной работе используется установка см. рис. 2, которая состоит из стального стержня с термопарами, нагревание конца которого производится в электропечи, источника питания, термопары и вольтметра. Меняя напряжение, приложенное к электропечи, можем изменить температуру конца стержня.

Количество тепла, даваемое печью в единицу времени, определяется по формуле 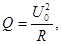где U₀ – определяемое вольтметром напряжение на концах обмотки печи . Температура печи (конца стержня) Т₁ также определяется термопарой. Теплота Q частично идёт на создание теплового потока q, обусловленного теплопроводностью стержня, частично – в окружающее печь пространство q_{1,_} так что

Q = q+ q_1.

Если удалить стержень из печи и, регулируя нагрев её, получить такую в ней же температуру Т₁, какая была в ней со стержнем, то ясно, что этим самым можно определить количество теплоты, идущее в единицу времени в окружающую печь среду, именно:

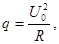
где U₁ – напряжение в печи без стержня. Таким образом, количество теплоты, поступающее в стержень равно:

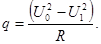
III. Проведение эксперимента и обработка результатов.

1. Измерить площадь поперечного сечения S, длину стержня ℓ и расстояние х от нагреваемого конца до каждой термопары.

2. Поместить конец стержня в электропечь и включить её. После установления теплового равновесия (показания термопар остаются неизменными) произвести запись показаний всех термопар и вольтметра.

3. Извлечь из печи стержень и ,регулируя нагревание печи, добиться того, чтобы термопара печи давала прежние показания, одновременно записать показания вольтметра. Измерения повторяют, не менее двух раз и вычисляют среднее значение. Результаты занести в таблицу.

4. Построить график зависимости 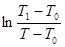от положения термопары относительно нагреваемого конца стержня, что даёт прямую линию, отвечающую уравнению (5).

5. По графику найти величину углового коэффициента а.

6. Подставляя его значение в формулу (8) и используя значение теплового потока q, определяемое формулой (10), найти искомую величину коэффициента теплопроводности.

7. Определить ошибку измерения коэффициента теплопроводности.

8. Повторить п. 2 – 7 для других значений напряжения печи.

9. Оформить результаты в виде таблицы.

Контрольные вопросы.

1. Почему основываясь на молекулярно – кинетических представлениях можно объяснить теплопроводность металлов? Чем переносится тепловая энергия в данном случае?

2. Какие физические величины связывают коэффициент теплопроводности, и как это уравнение называется?

3. От каких физических величин зависит коэффициент теплопроводности?

4. Как изменяется тепловой поток в зависимости от длины металлического стержня, и в каких единицах он измеряется?

5. Молекулярная физика и термодинамика имеет дело с равновесными состояниями тел и с обратимыми процессами. Как называется область физики, изучающая процессы, возникающие при нарушениях равновесия? Какие процессы носят название явлений переноса?