Общее уравнение плоскости

Ax+By+Сz-Ax₀-By₀-Сz₀=0

-Ax₀-By₀-Сz₀=D, где D=Ax+By+Сz

Ax+By+Сz+D=0

Частный случай:

Если D=0, то Ax+By+Сz=0(проходит ч/з 0;0)

Если A=0, то By+Сz+D=0

Если B=0, то Ax +Сz+D=0

Если C=0, то Ax+By+D=0

Если A=B=0, то Сz+D=0

Если A=C=0, то By+D=0

Если A=D=0, то By+Сz=0

Если B=D=0, то Ay+Сz=0

Взаимное расположение плоскостей.

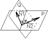
N₁,N₂-нормальные векторы плоскости.

P:A₁x+B₁y+C₁z+D₁=0

Q:A₂x+B₂y+C₂z+D₂=0

P^Q{A₁,B₁,C₁}

Q^N₂{A₂,B₂,C₂}

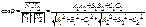
1)Пусть P^Q<=>N₁^N₂

A₁A₂+B₁B₂+C₁C₂=0 условие перпендик/ P^Q.

2) Пусть P^Q<=> N₁^N₂

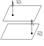
A₁/A₂=B₁/B₂=C₁/C₂- Условие II 2х плоскостей.

A₁/A₂=B₁/B₂=C₁/C₂=D₁/D₂- совпадения 2х плоск.

Канонич Ур-ие прямой в пространстве.

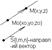
M₀M{x-x₀,y-y₀,z-z₀}

Чтобы точка МÎпрямой(или лежала на ней)

необх. и достаточно, чтобы M₀M||S

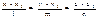
Уравнение прямой в пространстве,

проходящей ч/з 2 заданные точки.

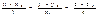
l m n

S{x₂-x₁,y₂-y₁,z₂-z₁}

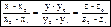
Прямая, как пересечение плоскостей.

Нахождение начальной