Бесконечно большая функция (б.б.ф.)
Определение 2.3. Функция 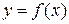 называется бесконечно большой (б.б.ф.) при
называется бесконечно большой (б.б.ф.) при 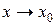 , если для любого числа
, если для любого числа 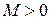 существует число
существует число 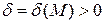 , что для всех
, что для всех 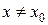 , удовлетворяющих неравенству
, удовлетворяющих неравенству 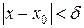 , выполняется неравенство
, выполняется неравенство 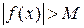 , т.е.
, т.е.
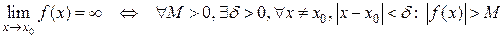 .
.
Например, функция 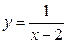 есть б.б.ф. при
есть б.б.ф. при 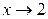 .
.
Если 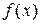 стремится к бесконечности при
стремится к бесконечности при 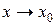 и принимает лишь положительные значения, то пишут
и принимает лишь положительные значения, то пишут 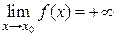 ; если лишь отрицательные значения, то
; если лишь отрицательные значения, то 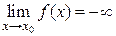 .
.
Аналогично определяются бесконечно большие функции (т.е. понятия бесконечного предела функции) при 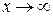 , или
, или 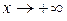 , или
, или 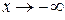 .
.
Бесконечно малые функции (б.м.ф.)
Определение 2.4. Функция 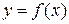 называется бесконечно малой (б.м.ф.) при
называется бесконечно малой (б.м.ф.) при 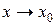 , если для любого положительного e найдется такое положительное число d, что для всех
, если для любого положительного e найдется такое положительное число d, что для всех 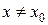 , удовлетворяющих неравенству
, удовлетворяющих неравенству 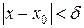 , выполняется неравенство
, выполняется неравенство 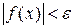 .
.
С помощью логических символов это определение можно записать следующим образом:
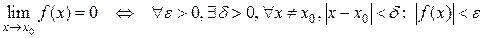 .
.
Например, функция 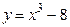 есть б.м.ф. при
есть б.м.ф. при 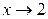 ; функция
; функция 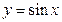 есть б.м.ф. при
есть б.м.ф. при 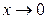 ;
;
Аналогично определяются бесконечно малые функции (т.е. понятия бесконечного предела функции) при 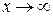 , или
, или 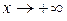 , или
, или 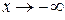 .
.
Бесконечно малые функции называют бесконечно малыми величинами или бесконечно малыми; обозначают обычно греческими буквами, т.е. 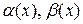 .
.
Пример 2.2. Показать, что функция
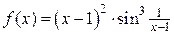
при 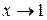 является бесконечно малой.
является бесконечно малой.
Решение. Так как 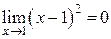 , то функция
, то функция 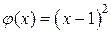 есть бесконечно малая при
есть бесконечно малая при 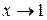 . Функция
. Функция 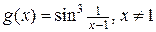 , ограничена, т.к.
, ограничена, т.к. 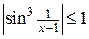 .
.
Функция 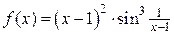 представляет собой произведение ограниченной функции
представляет собой произведение ограниченной функции 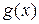 на бесконечно малую
на бесконечно малую 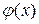 . Значит,
. Значит, 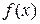 - бесконечно малая при
- бесконечно малая при 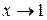 .
.
,
Бесконечно малые функции играют существенную роль в том, что понятие предела функции может быть сведено к понятию бесконечной малой. Имеет место следующая теорема, которую примем без доказательства
Теорема 2.1. Число A является пределом функции 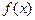 в точке
в точке 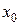 тогда и только тогда, когда имеет место равенство
тогда и только тогда, когда имеет место равенство
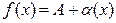 ,
,
где 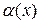 - б.м.ф. при
- б.м.ф. при 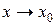 , т.е.
, т.е.
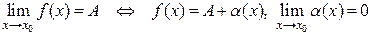 .
.
Теорема 2.2. Если функции 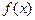 и
и 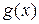 имеют в точке
имеют в точке 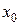 пределы A и B, т.е.
пределы A и B, т.е. 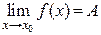 и
и 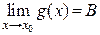 , то:
, то:
1) 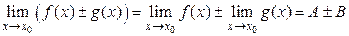 ;
;
2) 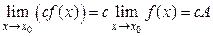 ;
;
3) 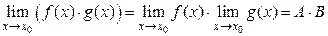 ;
;
4) 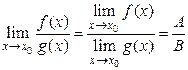 , где
, где 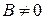 ;
;
Неопределенности
Если 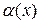 и
и 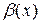 - б.м.ф. при
- б.м.ф. при 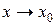 , то выражение
, то выражение 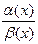 при
при 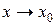 называется неопределенностью типа
называется неопределенностью типа 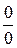 . Если
. Если 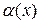 и
и 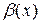 - б.б.ф. при
- б.б.ф. при 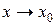 , то выражение
, то выражение 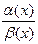 при
при 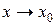 называется неопределенностью типа
называется неопределенностью типа 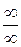 , а выражение
, а выражение 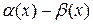 - неопределенностью типа
- неопределенностью типа 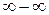 . Если
. Если 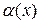 - б.м.ф., а
- б.м.ф., а 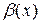 - б.б.ф. при
- б.б.ф. при 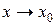 , то
, то 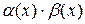 называется неопределенностью типа
называется неопределенностью типа 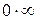 . Аналогично вводятся неопределенности типа
. Аналогично вводятся неопределенности типа 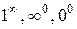 и т.д.
и т.д.
Раскрыть неопределенность – это значит найти предел соответствующего выражения (если он существует), что зависит от конкретных функция, входящих в выражения.
Рассмотрим приемы раскрытия некоторых неопределенностей.
1. Непосредственное нахождение предела
Пример 2.3. Вычислить
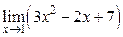 .
.
Решение.
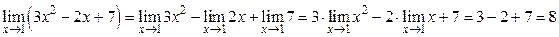 .
.
,
2. Преобразования, приводимые к сокращению дробей
Пример 2.4. Вычислить
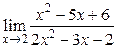 .
.
Решение.
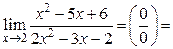 [раскладываем на множители числитель и знаменатель:
[раскладываем на множители числитель и знаменатель:
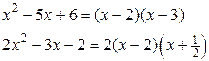 ] =
] =
= 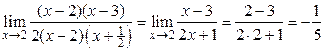 .
.
,
3. Деление на старшую степень x при 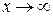
Пример 2.5. Вычислить
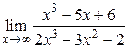 .
.
Решение.
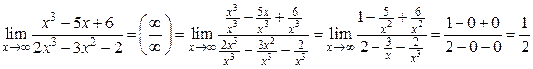 .
.
,
Пример 2.6. Вычислить
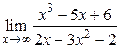 .
.
Решение.
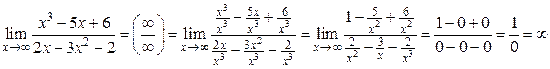 .
.
,
4. Сокращение с предварительным уничтожением иррациональности
Пример 2.7. Вычислить
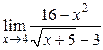 .
.
Решение.
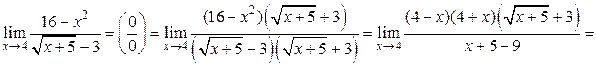
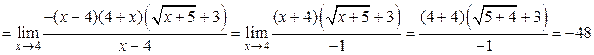 .
.
,
Не всякая функция, даже ограниченная, имеет предел. Например, функция 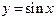 при
при 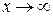 предела не имеет. Во многих вопросах анализа бывает достаточно только убедиться в существовании предела функции. В таких случаях пользуются признаками существования предела.
предела не имеет. Во многих вопросах анализа бывает достаточно только убедиться в существовании предела функции. В таких случаях пользуются признаками существования предела.
Теорема 2.3. (теорема о пределе промежуточной функции или теорема о «двух милиционерах») Если функция 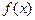 заключена между двумя функциями
заключена между двумя функциями 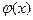 и
и 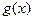 , стремящимися к одному и тому же пределу, то она также стремиться к этому пределу, т.е., если
, стремящимися к одному и тому же пределу, то она также стремиться к этому пределу, т.е., если
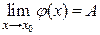 и
и 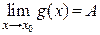 ,
, 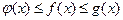 , то
, то
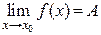 .
.
Замечательные пределы
Теорема 2.4. (I замечательный предел) Предел отношения синуса к его аргументу равен единице, когда аргумент стремится к нулю, т.е.
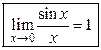 . (2.1)
. (2.1)
Пример 2.8. Найти
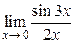 .
.
Решение. Первый способ. Имеем неопределенность типа 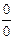 . Теорема о пределе дроби не применима. Обозначим
. Теорема о пределе дроби не применима. Обозначим 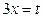 , тогда при
, тогда при 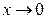 и
и 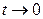 , поэтому
, поэтому
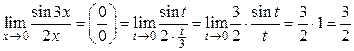 .
.
Второй способ.
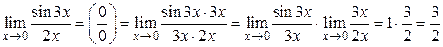 .
.
,
Пример 2.9. Найти
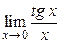 .
.
Решение.
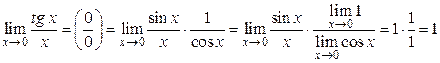 .
.
,
Теорема 2.5. (II замечательный предел)
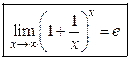 . (2.2)
. (2.2)
Если в равенстве (2.2.) положить 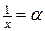 (
( 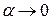 при
при 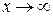 ), оно напишется в виде
), оно напишется в виде
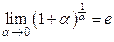 . (2.3)
. (2.3)
Равенство (2.3) тоже называется II замечательным пределом.
Пример 2.10. Найти
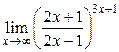 .
.
Решение.
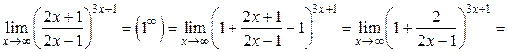
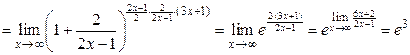 .
.
,
2.7.Сравнение бесконечно малых функций
Как известно, сумма, разность и произведение двух б.м.ф. есть функция бесконечно малая. Отношение же двух б.м.ф. может вести себя различным образом: быть конечным числом, быть бесконечно большой функцией, бесконечно малой или вообще не стремиться ни к какому пределу.
Две б.м.ф. сравниваются между собой с помощью их отношения.
Пусть 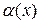 и
и 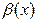 есть б.м.ф. при
есть б.м.ф. при 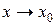 , т.е.
, т.е. 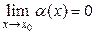 и
и 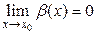 . Тогда:
. Тогда:
1) Если 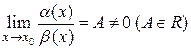 , то функции
, то функции 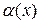 и
и 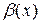 называются бесконечно малыми одного порядка. В этом случае пишут:
называются бесконечно малыми одного порядка. В этом случае пишут: 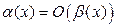 при
при 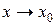 (читается: «
(читается: « 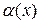 есть O большое от
есть O большое от 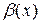 при
при 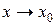 ).
).
2) Если 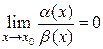 , то функция
, то функция 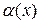 называется бесконечно малой более высокого порядка, чем
называется бесконечно малой более высокого порядка, чем 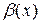 . В этом случае пишут:
. В этом случае пишут: 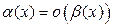 при
при 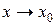 (читается: «
(читается: « 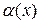 есть o малое от
есть o малое от 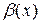 при
при 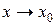 ).
).
3) Если 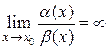 , то функция
, то функция 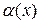 называется бесконечно малой более низкого порядка, чем
называется бесконечно малой более низкого порядка, чем 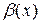 .
.
4) Если 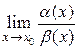 не существует, то функции
не существует, то функции 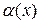 и
и 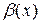 называются несравнимыми бесконечно малыми.
называются несравнимыми бесконечно малыми.
Например, при сравнении двух функций 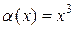 и
и 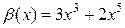 при
при 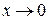 , получаем
, получаем 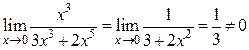 , значит, данные функции являются бесконечно малыми одного порядка, т.е.
, значит, данные функции являются бесконечно малыми одного порядка, т.е. 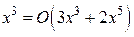 ; при сравнении двух функций
; при сравнении двух функций 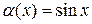 и
и 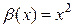 при
при 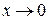 , получаем
, получаем 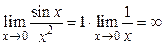 , значит, функция
, значит, функция 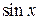 является бесконечно малой более низкого порядка, чем функция
является бесконечно малой более низкого порядка, чем функция 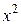 .
.
Пример 2.11. Можно ли сравнить функции 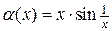 и
и 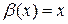 при
при 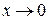 .
.
Решение. Функции 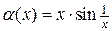 и
и 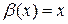 при
при 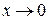 являются несравнимыми б.м.ф., так как предел
являются несравнимыми б.м.ф., так как предел 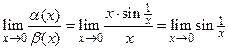 не существует.
не существует.
,
Отметим, что таковы же правила сравнения б.м.ф. при 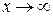 .
.
Среди бесконечно малых функций одного порядка особую роль играют так называемые эквивалентные бесконечно малые.
Если 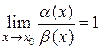 , то функции
, то функции 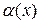 и
и 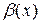 называются эквивалентнымибесконечно малыми при
называются эквивалентнымибесконечно малыми при 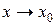 ; это обозначается так: a~b.
; это обозначается так: a~b.
Теорема 2.6. Если при 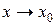
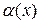 ~
~ 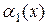 ,
, 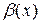 ~
~ 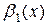 и существует
и существует 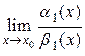 , то существует
, то существует 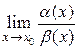 , причем
, причем
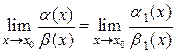 .
.
Для раскрытия неопределенностей типа 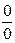 часто бывают полезным применять принцип замены бесконечно малых эквивалентными и другие свойства эквивалентных бесконечно малых функций. Как известно,
часто бывают полезным применять принцип замены бесконечно малых эквивалентными и другие свойства эквивалентных бесконечно малых функций. Как известно, 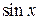 ~
~ 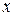 при
при 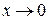 ,
, 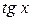 ~
~ 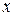 при
при 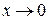 . Приведем еще примеры эквивалентных б.м.ф.
. Приведем еще примеры эквивалентных б.м.ф.
Пример 2.12. Покажем, что 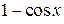 ~
~ 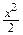 при
при 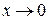 .
.
Решение.
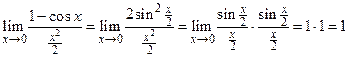 .
.
,
Пример 2.13. Найти
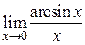 .
.
Решение.
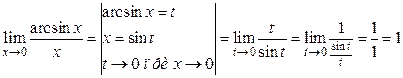 .
.
,
Ниже приведем важнейшие эквивалентности, которые используются при вычислении пределов:
1. 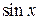 ~ ~ 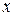 при при 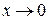 ; 2. ; 2. 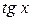 ~ ~ 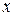 при при 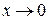 ; 3. ; 3. 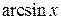 ~ ~ 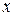 при при 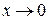 ; 4. ; 4. 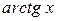 ~ ~ 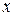 при при 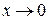 ; 5. ; 5. 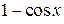 ~ ~ 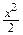 при при 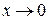 ; ; | 6. 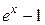 ~ ~ 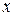 при при 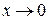 ; 7. ; 7. 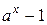 ~ ~ 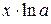 при при 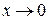 ; 8. ; 8. 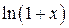 ~ ~ 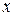 при при 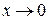 ; 9. ; 9. 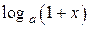 ~ ~ 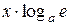 при при 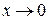 ; 10. ; 10. 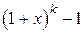 ~ ~ 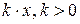 при при 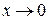 ; в частности, ; в частности, 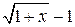 ~ ~ 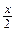 . . |
Пример 2.14. Найти
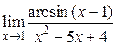 .
.
Решение. Так как 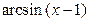 ~
~ 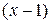 при
при 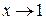 , то
, то
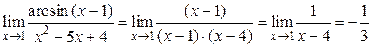 .
.
,
2.8.Односторонние пределы
В определении предела функции 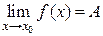 считается, что
считается, что 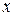 стремится к
стремится к 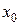 любым способом: оставаясь меньшим, чем
любым способом: оставаясь меньшим, чем 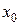 (слева от
(слева от 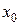 ), большим, чем
), большим, чем 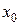 (справа от
(справа от 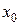 ), или колеблясь около точки
), или колеблясь около точки 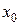 .
.
Бывают случаи, когда способ приближения аргумента 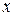 к
к 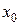 существенно влияет на значение предела функции. Поэтому вводят понятия односторонних пределов.
существенно влияет на значение предела функции. Поэтому вводят понятия односторонних пределов.
Определение 2.5. Число A1 называется пределом функции 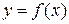 слева в точке
слева в точке 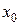 , если для любого положительного e найдется такое число
, если для любого положительного e найдется такое число 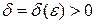 , что при
, что при 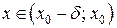 , выполняется неравенство
, выполняется неравенство 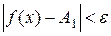 .
.
С помощью логических символов это определение можно записать следующим образом:
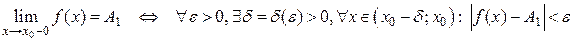 .
.
Или коротко: 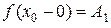 .
.
Аналогично определяется предел функции справа, который с помощью символов можно записать следующим образом:
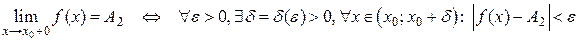 .
.
Или коротко: 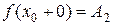 .
.
Пределы функции слева и справа называются односторонними.
Пример 2.15. Найти односторонние приделы функции 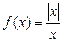 в точке
в точке 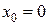 .
.
Решение. Имеем
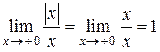 ;
; 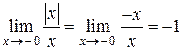 . ,
. ,
Связь между односторонними пределами и пределом функции в точке устанавливается следующей теоремой, которую примем без доказательства.
Теорема 2.7. Функция 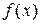 имеет предел в точке
имеет предел в точке 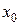 тогда и только тогда, когда в этой точке существует правый и левый пределы и они равны. В этом случае их общее значение и является пределом функции
тогда и только тогда, когда в этой точке существует правый и левый пределы и они равны. В этом случае их общее значение и является пределом функции 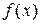 в точке
в точке 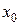 , т.е.
, т.е.
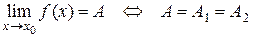 .
.
Следовательно, если односторонние пределы в точке существуют, но не равны, то предел функции в этой точке не существует. Так, функция 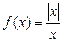 в точке
в точке 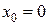 предела не имеет, поскольку
предела не имеет, поскольку 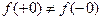 .
.
3. НЕПРЕРЫВНОСТЬ ФУНКЦИИ
