Кинетические коэффициенты в жидкости с точки зрения решеточной модели жидкости

В предыдущем параграфе была очень кратко изложена схема получения кинетических коэффициентов в жидкости с использованием методов, разработанных для газовой фазы.

В этом разделе рассмотрим кинетические коэффициенты жидкости, исходя из модели твердого тела. Наиболее известной здесь является теория Эйринга. Эту теорию часто называют теорией абсолютных скоростей реакций, так как первоначально она была использована именно для объяснения законов химической кинетики. Однако позднее данная теория с успехом была применена самим Г.Эйрингом и для вычисления коэффициентов переноса в жидкости, при этом было достигнуто простое и наглядное истолкование процесса. Приведем эти вычисления, но при этом опустим отдельные детали данного подхода, не принципиальные для излагаемого вопроса.

Примем, что частота переходов K молекулы за единицу времени через потенциальный барьер 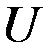пропорциональна^[3]:

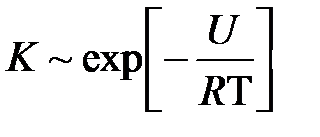. (3.15)

Рассмотрим дырочную модель жидкости: каждая молекула находится в своей ячейке и имеется некоторое количество дырок (рис.3.1).

Рассмотрим подробнее движение одной молекулы к расположенной около нее свободной ячейке (см. рис.3.1).

F

U

r

a

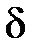DU=0

DU ¹0

Рис.3.1. Схематический рисунок, поясняющий модель Эйринга

Молекула должна преодолеть горловину (“протиснуться” между верхней и нижней частицами). Если внешняя сила равна нулю, то вид потенциальной энергии U относительно центра горловины симметричен.

Если же возникает сила F, то движение в одном из направлений предпочтительней (в рассматриваемом случае слева направо). Это связано с тем, что возникает добавочная энергия 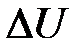, понижающая барьер U в одном направлении. Частота перескоков в направлении действия силы запишется тогда в виде

,

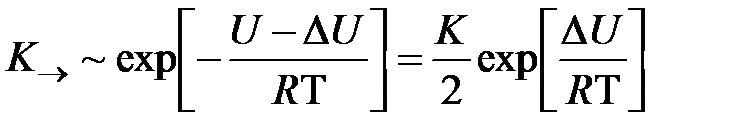а для обратного направления:

.

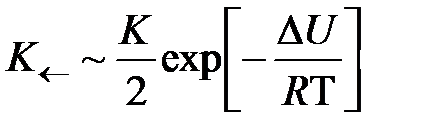Множитель 1/2 возникает по той причине, что при 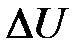=0 число прыжков частицей вправо и влево должно быть равно K.

Выразим 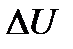. Пусть 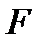– сила, действующая на единицу площади жидкости, тогда сила, действующая на одну молекулу, будет

,

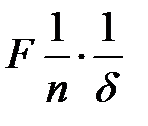где 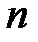- число молекул в единице объема, d - расстояние между соседними слоями. Соответственно работа над молекулой по перемещению ее на расстояние 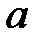(такой путь надо проделать, чтобы пролезть горловину) равна 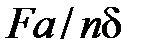. Эта работа и совпадает с энергией .

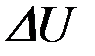Для общей скорости потока молекул относительно узлов решетки можно записать:

.

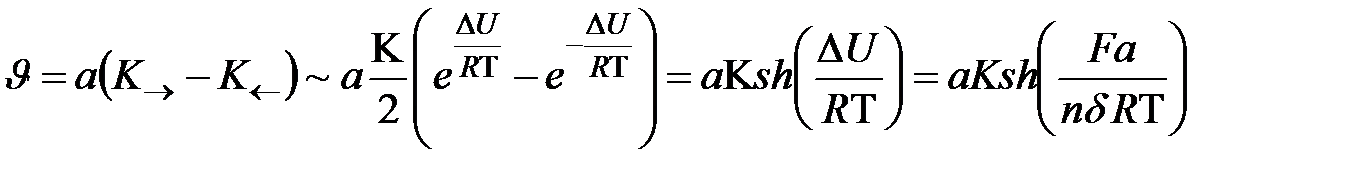Так как, исходя из формулы (3.1):

,

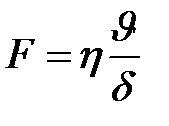то 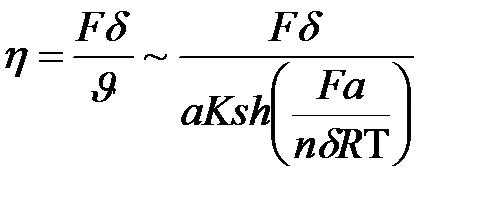. (3.16)

Из полученного соотношения (3.16) следует, что вязкость рассматриваемой жидкости зависит от внешней силы, т.е. жидкость является не ньютоновской. Отметим, что это редкий случай молекулярной теории переноса в которой заложена возможность описания такого поведения .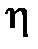

Упростим выражение (3.16), считая, что силы малы 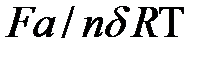<<1, тогда, раскладывая знаменатель в ряд, получим:

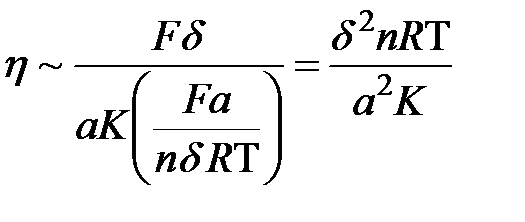. (3.17)

Будем приближенно считать, что 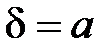, тогда

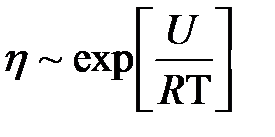. (3.18)

Таким образом, для расчета вязкости необходимо определить 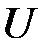. Эта энергия по физическому смыслу равна энергии взаимодействия молекулы со своим окружением, и, очевидно, что она должна быть близкой к энергии испарения (несколько меньшей, так как в данном случае молекула разрывает связи не со всем своим окружением, как при испарении). Эмпирически найдено, что она равна:

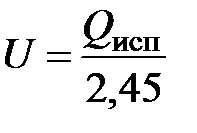, (3.19)

где Q_исп– теплота испарения моля жидкости.

По аналогии получим выражение для коэффициента диффузии. Рассмотрим две площадки 1 и 2 расположенные на некотором малом расстоянии d друг от друга (рис.3.2). Пусть 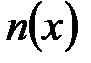– концентрация вещества, диффузия которого будет изучаться. Предположим, что в слое 1 концентрация равна 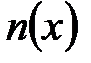, тогда в слое 2 из-за малости d концентрация равна 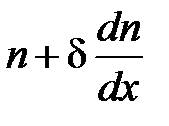(рис.3.2).

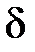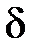n

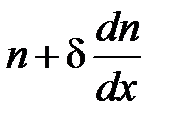Рис.3.2. Графическое пояснение вывода выражения для коэффициента диффузии

Пусть снова 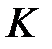– число перескоков барьера длиной d за единицу времени. Так как площадь, приходящаяся на одну молекулу, 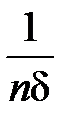, то общее число молекул в единице площади 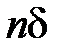, и поэтому общее число частиц, переходящих через единицу площади за единицу времени в направлении 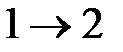, равно 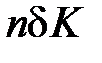. Для обратного направления эта величина, очевидно, равна 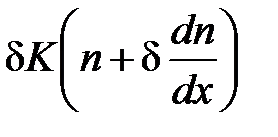. В результате суммарный поток частиц за единицу времени через единицу площади оказывается равным:

.

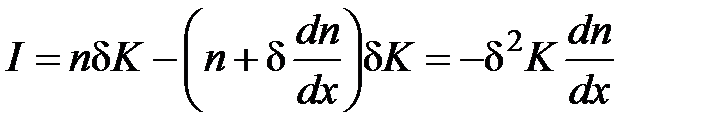Исходя из формулы (3.3):

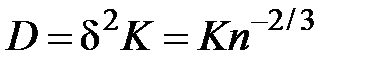. (3.21)

В последнем равенстве использовано, как и прежде, что d³=1/n. Формулу (3.21) также можно непосредственно использовать для вычисления коэффициента диффузии, принимая во внимание явное выражения для K [см. выражения (3.15),(3.19)].

Для вычисления коэффициента теплопроводности предположим, что жидкость имеет ячеечное строение. Пусть молекулы жидкости находятся в узлах кубической решетки и расстояние между ними .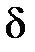

Пусть существует температурный градиент 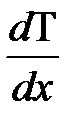. Будем считать, что средняя энергия молекулы в ячейке 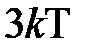(представляет собой некий трехмерный гармонический осциллятор). Тогда разность энергии между двумя смежными ячейками в направлении градиента равна - 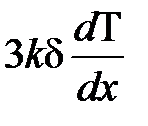. Предположим, что скорость передачи энергии равна скорости звука 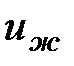. В результате энергия, переданная за единицу времени, равна - 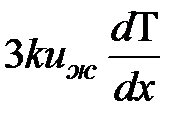(число элементов ряда в каком-нибудь направлении 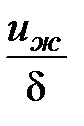умноженное на энергию, вносимую каждым элементом). Общее количество энергии через единицу площади и за единицу времени I_q равно энергии, переданной через отдельный ряд, умноженной на общее число рядов 1/d²:

.

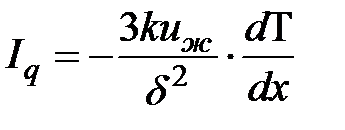Вспоминая уравнение (3.2) и используя, как и прежде, связь среднечисловой плотности n с d, получим

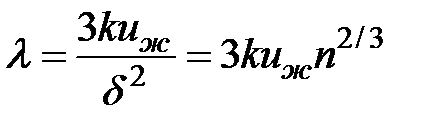. (3.22)

Формула (3.22) получила название формулы Бриджмена, она позволяет производить достаточно точный количественный расчет коэффициента теплопроводности в жидкости. Подобная формула была получена ранее. Однако приведенный здесь вывод представляется более последовательным, так как явно не использует формулу для теплопроводности в газе.