Атом в магнитном поле. Магнитные моменты электро-нов и атомов. Орбитальный и спиновой магнитные моменты

Все вещества, помещенные в магнитное поле, намагничиваются. Для объяснения намагничивания тел французский физик Андре-Мари Ампер предположил, что в молекулах вещества циркулируют круговые токи, которые называются молекулярными токами (микротоки). Каж-дый такой ток обладает магнитным моментом и создает в окружающем пространстве магнитное поле. В отсутствие внешнего магнитного поля молекулярные токи ориентированы беспорядочным образом, вследст-вие чего обусловленное ими результирующее поле равно нулю. Под действием внешнего магнитного поля магнитные моменты молекул приобретают преимущественную ориентацию в одном направлении, вследствие чего вещество (магнетик) намагничивается − его суммар-ный магнитный момент становится отличным от нуля. Магнитные поля

отдельных молекулярных токов в этом случае уже не компенсируют
друг друга, и возникает внутреннее магнитное поле индукцией Bi ,	ко-
торое накладывается на внешнее магнитное поле индукцией	B0.	Ин-
дукция результирующего магнитного поля равна:
B = B i + B .	(4.1.1)

Природа молекулярных токов стала понятней после того, как опытами английского физика Эрнеста Резерфорда было установлено, что атомы всех веществ состоят из положительно заряженного ядра и движущихся вокруг него отрицательно заряженных электронов.

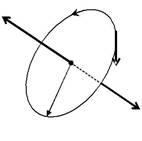
Пусть электрон движется со скоростью υ по орбите радиуса R (рис. 4.1.1). Через площадку, расположенную в любом месте на пути электрона, за один оборот переносится заряд

q = e,

(4.1.2)

где e – элементарный заряд. Следовательно, движущийся по орбите электрон образует круговой ток силы

I =	e	= en,	(4.1.3)
T

где Т и n – период и частота вращения электрона соответственно.

p_m I

q

O

R

υ

L₀

Рис. 4.1.1

Поскольку заряд электрона отрицательный, направление движе-ния электрона и направление тока противоположны. Магнитный мо-мент тока, создаваемого электроном, равен:

	pm = IS = enπR2.	(4.1.4)
Скорость движения электрона равна:
	υ = 2πnR.	(4.1.5)
С учетом формулы (4.1.5) получается:
	pm =	eυR	.	(4.1.6)
Момент p
, обусловленный движением электрона по орбите, на-
m
зывается орбитальным магнитным моментом электрона.
С другой стороны, движущийся по орбите электрон обладает мо-
ментом импульса, равным:
	L0= meυR,	(4.1.7)

где т_е – масса электрона.

Вектор момента импульса L₀ называют орбитальным моментом импульса электрона.Направления векторов p_m и L₀противоположны

(рис. 4.1.1).

Отношение магнитного момента элементарной частицы к ее мо-менту импульса называется гиромагнитным отношением. Для элек-

трона орбитальное гиромагнитное отношение равно:

	pm	= −	e	,	(4.1.8)
	L	2m
		e			p
С учетом взаимного расположения (направления моментов	и
L0противоположны)получаем					m

pm =−g орбL0,

(4.1.9)

где g_орб = _2m^e_e − орбитальное гиромагнитное соотношение.

Взаимосвязь магнитного момента и орбитального момента им-пульса лежит в основе магнитомеханических явлений, заключающих-ся в том, что вращение магнетика вызывает его намагничиванию и, наоборот, намагничивание магнетика приводит к его вращению . Су-ществование первого явления было экспериментально доказано аме-риканским физиком Сэмюэлем Барнеттом в 1909 году, второго – не-мецким физиком Альбертом Эйнштейном и голландским физиком Вандером Йоханнесем де Хаасом в 1915 году.

В основе опыта Эйнштейна и де Хааса лежат следующие сообра-жения. Если намагнитить стержень из магнетика, то магнитные мо-менты электронов установятся по направлению поля, механические моменты − против поля. В результате суммарный момент импульса электронов ∑L_i станет отличным от нуля (первоначально вследствие хаотической ориентации моментов отельных электронов он был равен нулю). Момент импульса системы «кристаллическая решетка и элек-троны» должен остаться без изменений (согласно закону сохранения момента импульса). Поэтому стержень приобретает момент импульса, равный ∑L_i и направленный противоположно суммарному моменту импульса электронов, и, следовательно, приходит во вращение.

Опыт Эйнштейна и де Хааса осуществлялся следующим образом (рис. 4.1.2). Тонкая железная проволочка подвешивалась на упругой нити и помещалась внутрь соленоида. Закручивание нити при намаг-ничивании образца постоянным магнитным полем получалось весьма малым. Для усиления эффекта был применен метод резонанса: по цепи соленоида пропускали переменный ток, частота которого под-биралась равной собственной частоте механических колебаний сис-темы. При этих условиях амплитуда колебаний достигала наиболь-ших значений, которые можно было измерить, наблюдая смещения светового зайчика , отраженного от зеркальца, укрепленного на нити. Из данных опыта было вычислено гиромагнитное отношение, кото-

рое оказалось равным − ^e . Таким образом, знак заряда носителей, m_e

создающих молекулярные токи, совпал со знаком заряда электрона. Однако полученный результат превысил ожидаемое значение гиро-магнитного отношения в два раза.

∼

Рис. 4.1.2

С. Барнетт приводил железный стержень в очень быстрое враще-ние вокруг его оси и измерял возникающее при этом намагничивание. Из результатов этого опыта С. Барнетт также получил для гиромаг-нитного отношения величину, в два раза большую.

В дальнейшем выяснилось, что, кроме орбитального момента им-

пульса, электрон обладает собственным моментом импульса L_S или

спином.Первоначально предполагалось,что он образуется вследствиевращения электрона вокруг собственной оси. В соответствии с этим соб-ственный механический момент электрона получил название спин (от английского to spin − вращаться). Однако в дальнейшем выяснилось, что спин является первичной характеристикой электрона, которую нельзя свести к более простым понятиям (как, например, масса и заряд).

Собственный магнитный момент электрона p_S связан со спином

спиновым гиромагнитным соотношением:
pS = −gS LS ,	(4.1.10)

где g_S = e 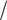m_e −спиновое гиромагнитное соотношение.

Спиновое гиромагнитное соотношение совпадает со значением, полученным в опытах Эйнштейна и де Хааса, а также Барнетта. От-сюда следует, что магнитные свойства железа обусловлены не орби-тальным, а собственным магнитным моментом электронов.

Спином обладают не только электроны, но и другие элементар-ные частицы. Собственным магнитным моментом обладают также яд-ра атомов (что обусловлено магнитными моментами входящих в со-став ядра элементарных частиц − протонов и нейтронов).

J =χH ,

Таким образом, магнитный момент атома слагается из орбиталь-ных и собственных моментов входящих в его состав электронов, а также из магнитного момента ядра.