Построение графиков функций
| № п/п | Пример ПП 16 4. Построение графиков функций |
| №19 | Исследуйте функцию 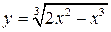 и постройте её график. 1). Функция определена при всех и постройте её график. 1). Функция определена при всех 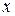 . Для нахождения точек пересечения с осями записываем уравнения . Для нахождения точек пересечения с осями записываем уравнения  и и 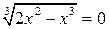 ; получаем, что ось ; получаем, что ось 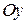 пересекается в точке с пересекается в точке с 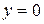 , а ось , а ось 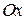 - в точках - в точках  и и 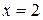 . 2). Точек разрыва нет. Так как нет точек разрыва 2-го рода, вертикальные асимптоты отсутствуют. Ищем параметры наклонных асимптот. . 2). Точек разрыва нет. Так как нет точек разрыва 2-го рода, вертикальные асимптоты отсутствуют. Ищем параметры наклонных асимптот. 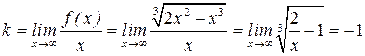 , , 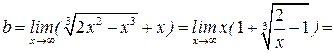 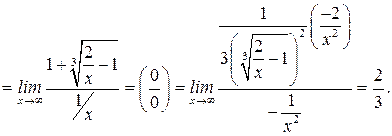 При вычислении второго предела использовано правило Лопиталя для раскрытия неопределённости типа При вычислении второго предела использовано правило Лопиталя для раскрытия неопределённости типа 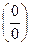 . Итак, у графика есть наклонная асимптота; её уравнение . Итак, у графика есть наклонная асимптота; её уравнение 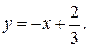 3). Находим производную: 3). Находим производную: 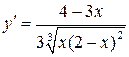 . Знак производной определяется знаком выражения . Знак производной определяется знаком выражения 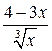 . Видим, что в области . Видим, что в области 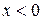 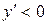 , при , при 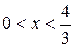 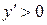 и при и при 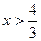 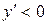 . Получаем, что в области . Получаем, что в области 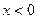 функция убывает, при функция убывает, при 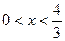 - возрастает и при - возрастает и при 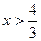 - убывает. Находим критические точки. - убывает. Находим критические точки. 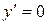 при при 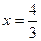 , , 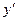 не существует при не существует при  , , 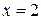 . При переходе через . При переходе через 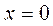 знак производной меняется с (-) на (+), т.е. это точка минимума. При знак производной меняется с (-) на (+), т.е. это точка минимума. При 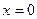 производная не существует, значит, минимум острый. производная не существует, значит, минимум острый. 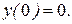 При переходе через вторую критическую точку При переходе через вторую критическую точку 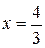 производная меняет знак с (+) на (-) , т.е. при производная меняет знак с (+) на (-) , т.е. при 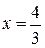 - максимум: - максимум: 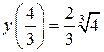 . При переходе через . При переходе через 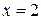 знак производной не меняется, значит экстремума нет. знак производной не меняется, значит экстремума нет. 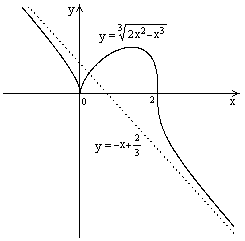 4) Находим вторую производную: 4) Находим вторую производную: 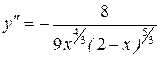 . Видим, что . Видим, что 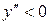 при при 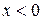 ; в этой области график выпуклый; ; в этой области график выпуклый; 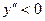 при при 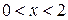 , т.е. интервал , т.е. интервал 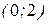 также является областью выпуклости. При также является областью выпуклости. При 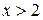 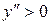 , следовательно, при , следовательно, при 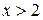 график вогнут. Найдём точки перегиба. Вторая производная не существует при график вогнут. Найдём точки перегиба. Вторая производная не существует при  и при и при 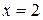 . При переходе через первую точку знак . При переходе через первую точку знак 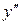 не меняется, а при переходе через вторую – меняется. Итак, точкой перегиба является точка с координатами не меняется, а при переходе через вторую – меняется. Итак, точкой перегиба является точка с координатами 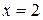 , , 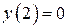 . . |
Определение скорости возрастания и убывания функций
Скорость роста линейной функции 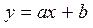 постоянна и равна
постоянна и равна 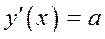 , квадратичной функции – линейна, и вообще, производная степенной функции, являясь меньшей степенью, растет медленнее, чем сама функция; скорость роста показательной функции пропорциональна значению самой функции, так как
, квадратичной функции – линейна, и вообще, производная степенной функции, являясь меньшей степенью, растет медленнее, чем сама функция; скорость роста показательной функции пропорциональна значению самой функции, так как 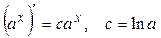 .
.
| № п/п | Пример ПП 16 5. Определение скорости возрастания и убывания функций |
| №20 | Какая из функций 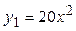 или или 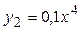 растет быстрее при больших растет быстрее при больших 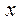 ? При ? При 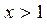 функция функция 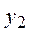 растет быстрее, так как растет быстрее, так как 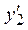 ~ ~ 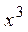 , а , а 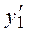 ~ ~ 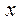 . Определим, начиная с каких значений аргумента . Определим, начиная с каких значений аргумента 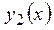 становится больше становится больше 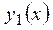 . Рассмотрим . Рассмотрим 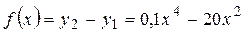 при при 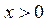 . . 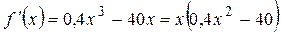 , , 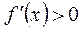 при при 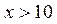 , функция , функция 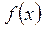 возрастает, значит, возрастает, значит, 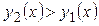 , т.е. функция , т.е. функция 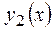 растет быстрее, начиная с растет быстрее, начиная с 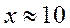 . . |
Доказательство неравенств с помощью производной
Если в точке 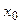 выполняется условие
выполняется условие 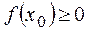 и для всех
и для всех 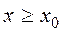 выполняется условие
выполняется условие 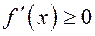 , то для всех
, то для всех 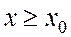 верно неравенство
верно неравенство 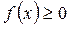 .
.
| № п/п | Пример ПП 16 6. Доказательство неравенств с помощью производной |
| №21 | Докажите неравенство: 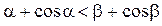 при при 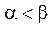 . Рассмотрим . Рассмотрим 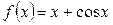 . Докажем, что . Докажем, что 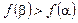 при при 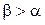 , т.е. что эта функция является возрастающей. , т.е. что эта функция является возрастающей. 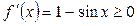 , т.к. , т.к. 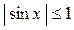 , значит, , значит, 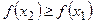 , если , если 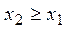 . Это доказывает неравенство в случае строгого возрастания аргумента. . Это доказывает неравенство в случае строгого возрастания аргумента. |
