Следствия преобразований Лоренца

1. Сокращение расстояний.

Пусть подвижная система перемещается вдоль оси х со скоростью V₀ и в ней находится стержень длиной l₀. В неподвижной системе находится цепочка наблюдателей с синхронизированными часами. Пусть для наблюдателя с координатой х₂ время пролета переднего конца совпало со временем пролета заднего конца мимо наблюдателя с координатой х₁. Подставим в формулу длины стержня 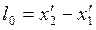координаты по преобразованиям Лоренца, получим 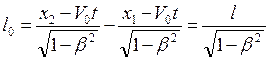. Откуда получим

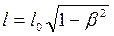. (13.3)

Длина движущегося стержня оказывается короче неподвижного стержня. В направлении движения линейные размеры тела сокращаются тем больше, чем больше скорость движения.

2. Увеличение длительности промежутков времени.

Пусть в подвижной системе отсчета происходит какой-нибудь процесс длительностью 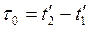в некоторой точке с координатой х′. Длительность этого процесса для наблюдателя в неподвижной системе отсчета 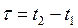. Подставив время начала и конца процесса по формулам Лоренца, получим 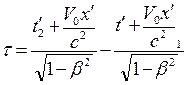. Откуда получим

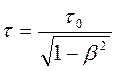. (13.4)

Время τ₀, отсчитанное по часам, которые движутся вместе с телом, называется собственным временем. Из (13.4) следует, что собственное время минимально. Это следствие можно сформулировать как утверждение, что движущиеся часы идут медленнее, чем покоящиеся часы.

Известно, что среднее собственное время жизни мезонов в лаборатории около двух микросекунд. Мезон, рожденный в верхних слоях атмосферы Земли, даже двигаясь с предельной скоростью, пролетит только 660 м, а регистрируется около поверхности Земли. Потому, что для земного наблюдателя время жизни летящего мезона в много раз больше собственного времени жизни.

В связи с явлением замедления времени возник «парадокс близнецов» Пусть первый из них остается на Земле и наблюдает, как улетающий в ракете брат не старится. То же самое наблюдает космонавт, для которого брат на Земле остается молодым. Кто из них прав? Ответ может быть получен, если космонавт вернется на Землю. Но при повороте корабль становится неинерциальной системой отсчета в отличие от Земли, и получить ответ в рамках СТО невозможно.

3. Релятивистский закон сложения скоростей

Рассмотрим материальную точку, движущуюся в системе отсчета К' со скоростью 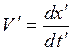вдоль оси x′. Определим скорость этой точки в неподвижной системе отсчета К, для которой 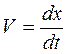. Дифференцируя формулы преобразований Лоренца (13.2), получим

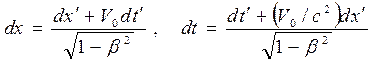. (13.5)

Разделив выражения (13.5) друг на друга, получим закон сложения скоростей

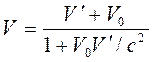. (13.6)

Например, относительно лаборатории частица летит со скоростью, близкой к скорости света (V₀= c). В направлении движения она излучает фотон (V′ = c). По закону сложения скоростей (13.6) получим, что скорость фотона относительно лаборатории опять равна V= с. Что и следовало ожидать, согласно второму постулату СТО. При скоростях движения малых по сравнению со скоростью света полученные формулы переходят в закон сложения скоростей Галилея 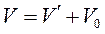.