Линейные ДУ высших порядков с постоянными коэффициентами.
Пример решения типового расчета по теме
«Дифференциальные уравнения и системы»
Дифференциальные уравнения первого порядка.
1. Найти частное решение, удовлетворяющее заданному начальному условию (решить задачу Коши):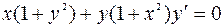 
; 
.
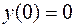Решение.
Найдем сначала общее решение данного ДУ.
Заменим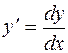 
и запишем уравнение в симметричной форме:
) 
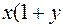
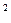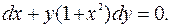
(1)
Это уравнение является дифференциальным уравнением с разделяющимися 
переменными (Р.П.), т.к. коэффициентами при дифференциалах являются функции только одной переменной.
Разделим переменные в (1), умножив обе части ДУ на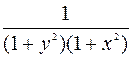 
, тогда уравнение примет вид: 
.
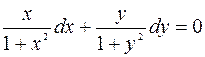Интегрируя, получим:
.
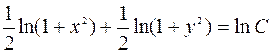( Произвольную постоянную удобно обозначить через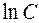 
).
Используя свойства логарифмов, запишем общее решение ДУ в виде:
. 
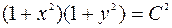Найдём частное решение, удовлетворяющее начальному условию
: 
.
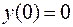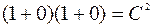
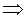
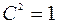Итак,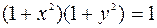 
– частное решение.
Ответ: .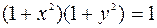
2. Найти общее решение ДУ: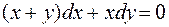 
.
Решение.
Данное уравнение является однородным ДУ; разделив на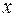 
, его можно записать в виде:
, 
.
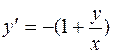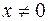Сделаем замену искомой функции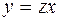 
, где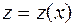 
– новая искомая функция. Получим:
;
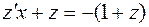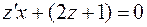или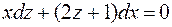 
(Р.П.)
Разделим переменные, умножив обе части ДУ на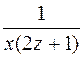 
.
Получим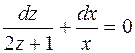 
. Интегрируя, находим
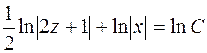или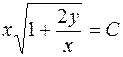 
– общий интеграл ДУ.
Ответ: .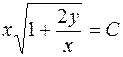
3. Найти общее решение ДУ: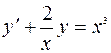 
.
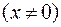Решение.
Это – линейное уравнение относительно неизвестной функции и её производной. Используем метод Бернулли.
Будем искать общее решение в виде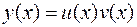 
, где 
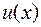и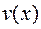 
– неизвестные функции аргумента .
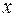Подставим решение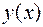 
в уравнение:
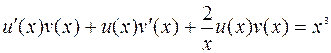или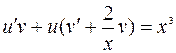 
.
Выберем функцию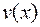 
так, чтобы 
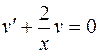, тогда для функции 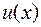получим уравнение: 
.
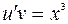Решаем систему: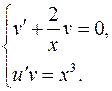 
Замечание: в первом уравнении находим любое частное решение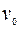 
, а во втором – общее решение.
1) 
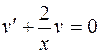
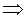
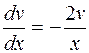(Р.П.)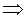 
.
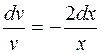
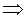
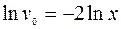
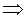
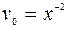(Произвольную постоянную берём равной нулю!).
2) 
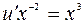
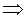
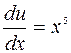
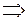
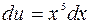
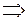
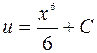. Следовательно, 
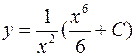– общее решение ДУ.
Ответ: .
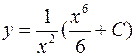4. Найти общее решение ДУ: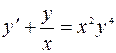 
.
Решение.
Это уравнение Бернулли. Оно приводится к линейному уравнению подстановкой: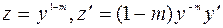 
.
У нас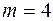 
; 
.
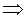
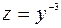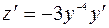Подставляем в данное уравнение:
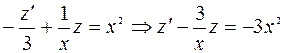– это линейное уравнение относительно 
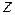и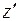 
.
Решаем полученное уравнение методом Бернулли.
Делаем подстановку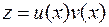 
:
;
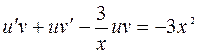
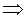
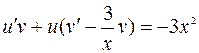
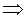
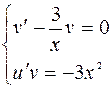1) 
;
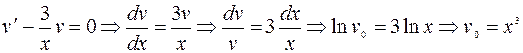2) 
;
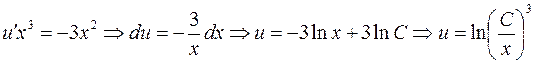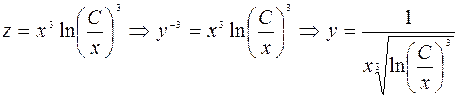–общее решение.
Ответ: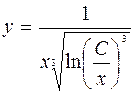 
.
5. Найти общее решение ДУ: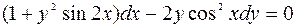 
.
Решение.
Убедимся, что данное ДУ является дифференциальным уравнением в полных дифференциалах.
Имеем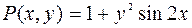 
; 
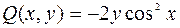, тогда
; 
.
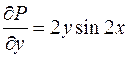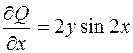Видим, что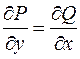 
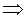это ДУ в полных дифференциалах, т.е. левая часть уравнения является полным дифференциалом некоторой функции 
.
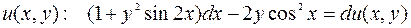Общее решения будет иметь вид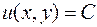 
.
Найдем функцию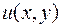 
с помощью формулы:
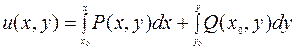, где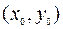 
– любая точка, для которой интегралы имеют смысл.
Возьмём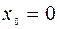 
и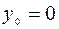 
. Тогда
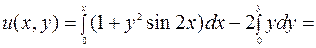
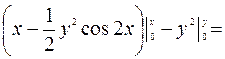
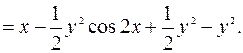
Следовательно,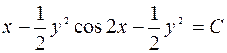 
– общий интеграл ДУ.
Ответ: .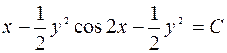
Дифференциальные уравнения высших порядков.
ДУ, допускающие понижение порядка.
6. Найти общее решение ДУ: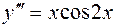 
.
Решение.
Данное уравнение является дифференциальным уравнением третьего порядка, допускающее понижение порядка непосредственным интегрированием.
=
= 
.
= 
= 
= 
= 
.
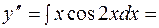
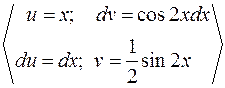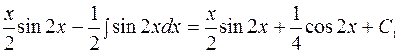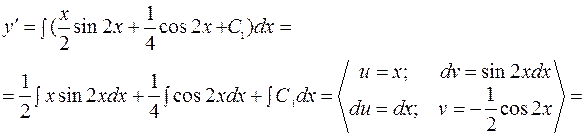
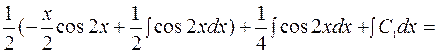
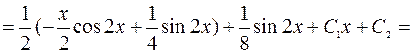
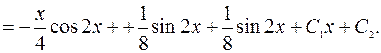
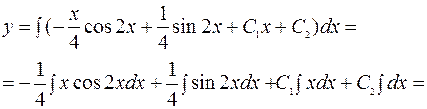
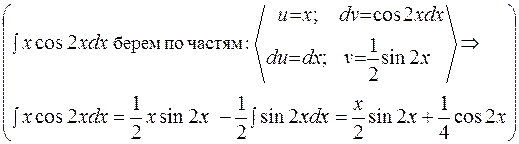
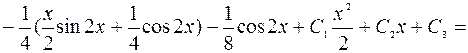
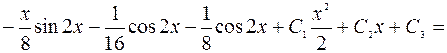
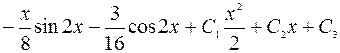Ответ: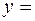 
.
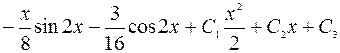7. Найти общее решение ДУ: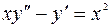 
.
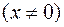Решение.
Данное ДУ второго порядка не зависит явно от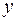 
, следовательно, оно допускает понижение порядка.
Разделим уравнение на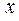 
: 
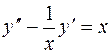. Заменим 
:
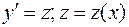Получим ДУ первого порядка относительно функции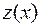 
:
.
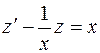Это уравнение линейное Применяем метод Бернулли:
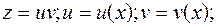
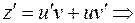
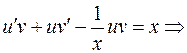
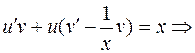
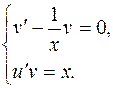
1) 
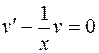
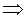
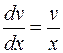(Р.П.)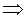 
.
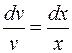
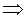
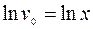
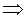
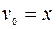2) 
.
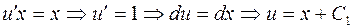Следовательно,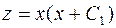 
, т.е. 
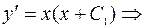интегрируя, получим 
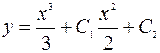– общее решение.
Ответ: .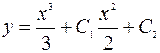
8. Найти частное решение, удовлетворяющее заданному начальному условию (решить задачу Коши):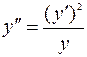 
; 
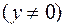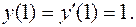
Решение.
Данное ДУ не зависит явно от 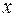. Понизим порядок уравнения, сделав замену
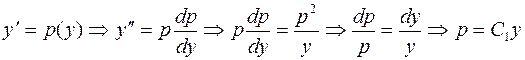; т.е. 
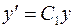или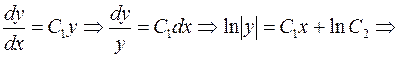 
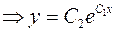– общее решение.
Подставим начальные условия: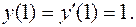
Получим систему: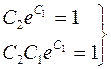 
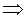
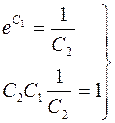
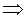
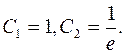
Значит,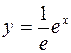 
или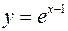 
– искомое частное решение.
Ответ: .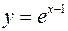
Линейные ДУ высших порядков с постоянными коэффициентами.
9. Найти общее решение ДУ: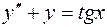 
.
Для решения данного неоднородного ДУ второго порядка применим метод вариации произвольных постоянных (см. лекцию).
Составим характеристическое уравнение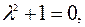 
найдем его корни 
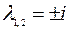(характеристические числа).
Тогда общее решение соответствующего однородного ДУ будет иметь вид:
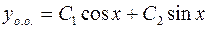, где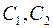 
– произвольные постоянные.
Будем искать общее решение неоднородного ДУ в ви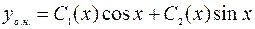де:
, где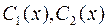 
– неизвестные функции.
Составим систему:
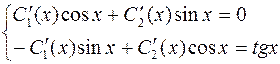(см. лекцию).
Находим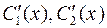 
из полученной системы (например, методом Крамера):
.
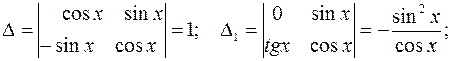
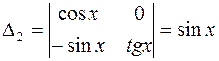Тогда,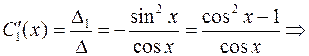 
;
.
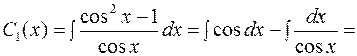
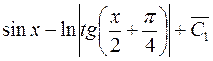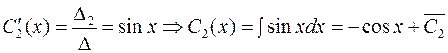Отсюда общее решение неоднородного ДУ будет иметь вид:
= 
.
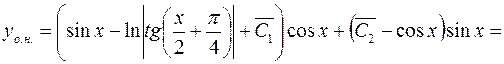
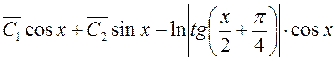Переобозначим произвольные постоянные.
Ответ: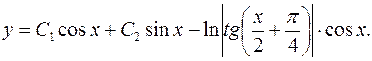 
10. Найти частное решение, удовлетворяющее заданному начальному условию (решить задачу Коши): 
, 
.
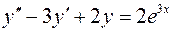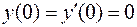Решение.