Линеаризованное обтекание тупого угла

Глава 5

ПЛОСКИЕ ИЗОЭНТРОПИЧЕСКИЕ

ТЕЧЕНИЯ ГАЗА

В пространстве движущегося газа по большому счету, за исключением некоторых достаточно ограниченных областей (пограничный слой, след за телом и др.), имеет место безвихревое, или потенциальное течение. Выясним, при каком условии течение можно считать потенциальным, т. е. при каком условии в потоке будут отсутствовать вихри.

Рассмотрим какую-нибудь линию тока аА (рис. 5.1). Проведем касательную к линии тока в точке а (совпадает с направлением вектора скорости 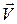) и внутреннюю нормаль n. Уравнение движения в проекции на нормаль n запишется следующим образом:

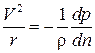, (5.1)

где r = Оа – радиус кривизны линии тока; 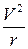– центростремительное ускорение. Вдоль линии тока полная удельная энергия и энтропия не изменяют своей величины, т. е. 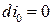и dS = 0.

Допустим, что при переходе от одной линии тока аА к другой bВ, расположенной на расстоянии 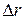от аА, полная удельная энергия 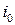и энтропия газа 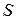изменяются. То есть

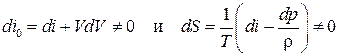. (5.2)

Исключив из уравнений (5.2) 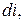получим 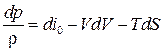. Тогда 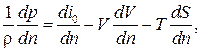и после подстановки в уравнение движения (5.1) имеем следующее:

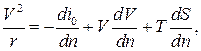или .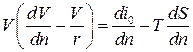

Выражение в скобках 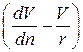есть не что иное, как удвоенная угловая скорость 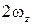. Из условия потенциальности (вращательное движение отсутствует) 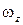= 0, следовательно, .

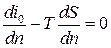Это равенство в общем случае выполняется, есл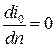и и .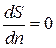

Случай выполнения этого равенства пр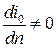и и 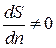не представляет интереса, так как он соответствует движению с линиями тока в виде либо концентрических окружностей, либо параллельных прямых.

Таким образом, поток газа можно считать потенциальным, если полная удельная энергия и энтропия при переходе от одной линии тока к другой не изменяются.

Основное дифференциальное уравнение плоского

потенциального потока газа

Рассмотрим плоский потенциальный газовый поток (установившееся течение). Уравнение неразрывности для такого течения имеет вид 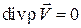, которое для плоского потока запишется как 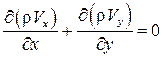. Проведя дифференцирование в этом уравнении, получаем

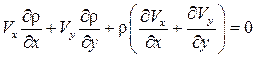. (5.3)

Выразим 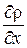и 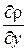через проекции скорост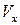и и 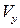. Считая движение баротропным 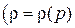, где 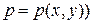, можно записать, что

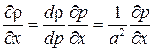и .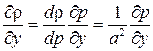

Заменим в этих выражениях 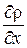и 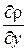через уравнения Эйлера (3.6) и (3.7) с учетом малости массовых сил, т. е. ,

,

.

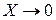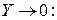
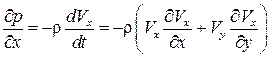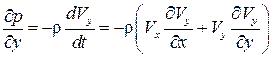Тогда имеем следующее:

,

.

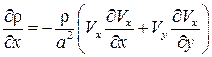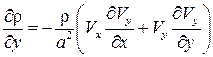Полученные выражения подставим в уравнение (5.3) и приведем его к следующему виду:

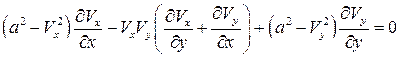. (5.4)

Учтем, что для потенциального потока 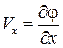, , 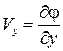и уравнение (5.3) примет вид

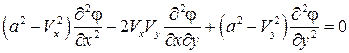. (5.5)

Уравнение (5.5) представляет собой основное дифференциальное уравнение газовой динамики для плоского потенциального установившегося газового потока. Это нелинейное дифференциальное уравнение второго порядка в частных производных относительно неизвестной функции 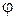. Однако коэффициенты при вторых производных в явном виде от координат х и y не зависят, поэтому уравнение (5.5) называют квазилинейным дифференциальным уравнением.

Для решения уравнения применяют два метода:

1) метод малых возмущений (метод линеаризации), который широко используется при исследовании обтекания тонких тел при малых углах атаки как в дозвуковом, так и в сверхзвуковом потоке и позволяет получить решение в аналитическом виде;

2) метод характеристик – численный метод, который применяется для определения поля скоростей в сверхзвуковом потоке.

Метод малых возмущений

Степень возмущения потока вблизи тела определяется относительной толщиной тела и его ориентацией в пространстве. Рассмотрим основные положения метода малых возмущений на примере обтекания тонкого профиля под малым углом атаки 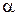. Поток около такого профиля мало отличается от плоскопараллельного невозмущенного потока, имеющего скорость 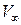. 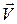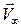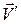Тогда представим скорость около профиля как сумму векторов и , где 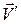– скорость возмущения. На этом основании составляющие скорости 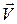вблизи профиля равны (ось ОX направлена вдоль вектора ):

,

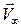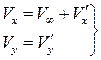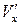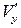где и – составляющие скорости возмущения ( , ).

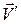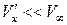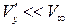Утверждение о малости возмущений справедливо везде, за исключением критической точки. В ее окрестности скорость потока равна нулю, т. е. 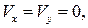и составляющая скорости возмущения 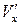равна по величине 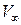и противоположна ей. Предположим, что малому возмущению скорости соответствуют также малые изменения давления, плотности и температуры.

Сущность метода малых возмущений (метода линеаризации) заключается в том, что во всех формулах удерживаются только члены первого порядка малости (вторыми и более высокими степенями малых величин 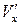, 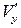и т. д. можно пренебречь).

Произведем линеаризацию уравнения (5.5). Рассмотрим вначале квадрат скорости:

.

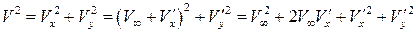Оставляя только величины не ниже первого порядка малости, получаем 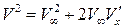. Тогда выражение для скорости потока 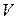будет иметь вид

.

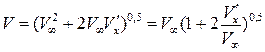Так как по условию 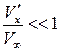, то используем известный из математики прием приближенного вычисления подобного выражения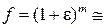 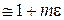(при условии 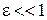). Таким образом, окончательно получаем

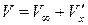. (5.6)

Аналогичные преобразования проведем с выражением для скорости звука:

.

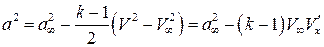То есть 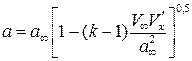. В окончательном виде

.

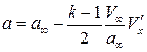Сравним между собой числа Маха потока около профиля 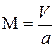и в невозмущенном потоке 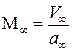, используя положения метода малых возмущений:

.

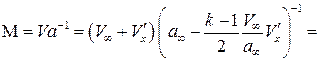
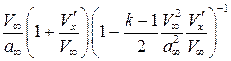Применив уже использовавшийся метод приближенного вычисления, ввиду малости дроби во второй скобке, получим

.

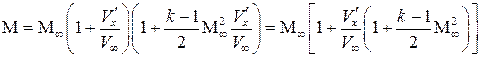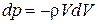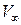Найдем давление в возмущенном потоке. Из уравнения Бернулли (3.30) . Интегрируем в пределах для давления от до и для скорости от до 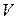. Тогда .

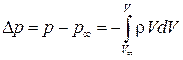Произведение 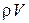(удельный расход через единицу площади) для невозмущенного потока равно 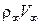, а для возмущенного потока равно 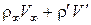. Произведем замену 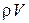под интегралом на его среднее значение:

,

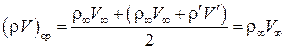и после интегрирования получим

.

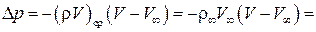
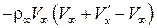В результате, окончательно получаем

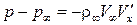. (5.7)

Выражение (5.7) представляет собой линеаризованное уравнение Бернулли.

Для линеаризации основного дифференциального уравнения газовой динамики (5.5) заменим в нем 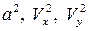и 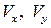через их линеаризованные выражения. Тогда с принятой точностью

.

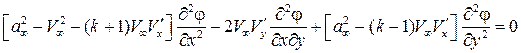Определим порядок величины вторых производных от потенциала скорости. Так 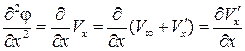, т. е. 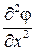имеет первый порядок малости. То же самое можно сказать и о других производных, входящих в линеаризуемое уравнение. Отбрасывая члены второго порядка малости, после деления на 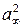получаем

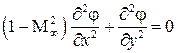, (5.8)

т. е. линейное дифференциальное уравнение.

Рассмотренный метод упрощения и преобразования исходного нелинейного дифференциального уравнения (5.5) называют методом линеаризации, а сам поток, описываемый уравнением (5.8), – линеаризованным потоком.

В случае трехмерного потока газа линеаризованное уравнение движения можно записать по аналогии с уравнением (5.8) в виде

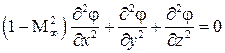. (5.8а)

Уравнения (5.8) и (5.8а) справедливы как для дозвуковых ( 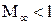), так и для сверхзвуковых ( 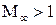) скоростей. Однако методы их решения различны и будут рассмотрены далее и для дозвуковых, и для сверхзвуковых скоростей.

Линеаризованное обтекание тупого угла

Сверхзвуковым потоком

Рассмотрим обтекание тупых углов АОВ (рис. 5.2), мало отличающихся от 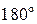, сверхзвуковым потоком газа в линейной постановке. Угол поворота потока будем считать положительным ( 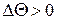), если угол АОВ больше 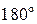(рис. 5.2, а), и отрицательным ( 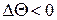), если угол АОВ меньше 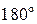(рис. 5.2, б).

Проводя линию возмущения 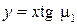из вершины угла О, получим области невозмущенного (I) и возмущенного (II) течений.

В области I скорость всюду постоянна и равна 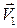, в области II скорость равна 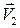также для всей области. Вектор 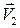повернут на угол 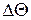по отношению к 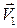. Считая течение газа в обеих областях потенциальным, введем потенциал скорости возмущения .

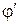Граничными условиями задачи являются следующие:

1) в области I, где 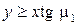, 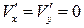и ;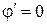

2) в области II ( 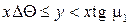) потенциал возмущения .

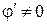а б

Рис. 5.2. Схемы линеаризованного обтекания тупого угла:

а – угол больше 180^о; б – угол меньше 180^о

Рассмотрев треугольники скоростей с учетом малости угла поворота потока ( 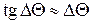) и обращая внимание на направления (знак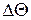и) и 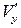, имеем следующее:

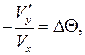или .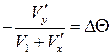

Пренебрегая произведением 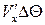как величиной второго порядка малости, получим выражение для расчета составляющей скорости :

.

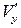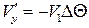Потенциал скорости возмущения 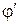удовлетворяет уравнению (5.8), общим решением которого является функция

.

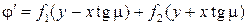В обоих вариантах рассматриваемой задачи частное решение 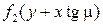не имеет физического смысла, так как линия возмущений 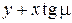равна нулю или наклонена навстречу набегающему потоку, или оказывается вне потока (уходит внутрь поверхности). Таким образом, общее решение имеет вид

.

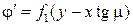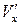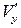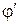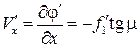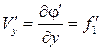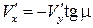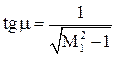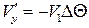Запишем составляющие скорости и через потенциал : , . Отсюда получаем . С учетом того, что и , выражение для 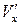примет вид 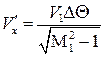. Таким образом, получаем систему уравнений для определения составляющих скорост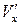и и :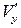

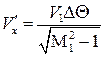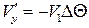, . (5.9)

Как видно из выражений (5.9), характер изменения скорости течения газа при обтекании угла АОВ зависит от знака угла поворота потока:

– при 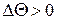: 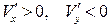, 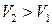– течение разрежения (рис. 5.2, а);

– при 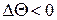: 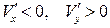, 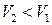– течение уплотнения (рис. 5.2, б).

Найдем изменение давления при обтекании угла АОВ. Воспользуемся линеаризованным уравнением Бернулли (5.7) в виде 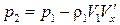. Отсюда, с учетом полученного решения (5.9),

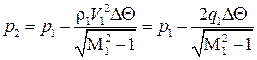, (5.10)

где 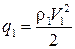– скоростной напор потока до начала поворота. Запишем выражение для коэффициента давления:

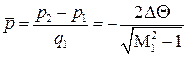. (5.10а)

Выражение (5.10) показывает, что при обтекании угла, большего 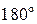( 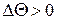), давление уменьшается, а при обтекании угла, меньшего 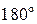( 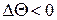), давление увеличивается, что находится в полном соответствии с физической картиной течения.

Метод характеристик