Системы линейных дифференциальных уравнений с постоянными коэффициентами
Определение
Совокупность уравнений вида
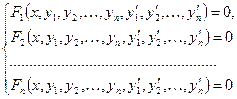 | (8.7.1) |
где 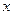 –независимая переменная,
–независимая переменная, 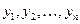 – искомые функции,
– искомые функции, 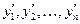 – их производные, называется системой дифференциальных уравнений первого порядка.
– их производные, называется системой дифференциальных уравнений первого порядка.
Система дифференциальных уравнений, разрешенных относительно производных от неизвестных функций, называется нормальной системой дифференциальных уравнений и имеет следующий общий вид:
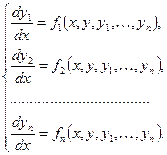 . . | (8.7.2) |
Совокупность 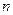 функций
функций
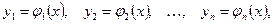 | (8.7.3) |
определенных в интервале 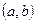 , называется решением нормальной системы (8.7.2), если эти функции при подстановке в уравнение системы (8.7.2) обращают их в тождество.
, называется решением нормальной системы (8.7.2), если эти функции при подстановке в уравнение системы (8.7.2) обращают их в тождество.
Теорема (Коши)
Пусть для системы дифференциальных уравнений первого порядка (8.7.2) выполняются следующие условия:
- функции 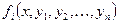 ,
, 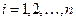 определены и непрерывны по всем аргументам в замкнутой области
определены и непрерывны по всем аргументам в замкнутой области 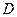 ,
,
- частные производные 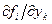 непрерывны в области
непрерывны в области 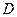 .
.
Тогда существует одна и только одна система решений уравнений (2):
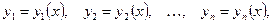 , , | (8.7.4) |
определенная в некоторой окрестности точки 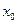 и удовлетворяющая в этой точке заданным начальным условиям:
и удовлетворяющая в этой точке заданным начальным условиям:
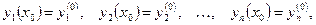 . . | (8.7.5) |
Условия (8.7.5) называются начальными условиями решения, а задача отыскания решения по заданным начальным условиям – задачей Коши.
Совокупность n функций
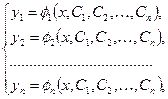 | (8.7.6) |
зависящих от 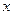 и
и 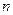 произвольных постоянных
произвольных постоянных 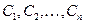 , будем называть общим решением системы (8.7.2) в некоторой области
, будем называть общим решением системы (8.7.2) в некоторой области 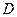 , если при любых значениях постоянных
, если при любых значениях постоянных 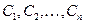 эти функции представляют решение системы и если любое решение этой системы может быть записано в виде (8.7.6) при некоторых значениях постоянных
эти функции представляют решение системы и если любое решение этой системы может быть записано в виде (8.7.6) при некоторых значениях постоянных 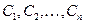 .
.
Совокупность 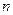 функций
функций
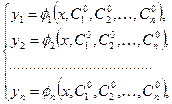 | (8.7.7) |
получающееся из общего решения (6) системы (8.7.2) при определенных значениях постоянных 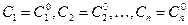 будем называть частным решением системы (8.7.2).
будем называть частным решением системы (8.7.2).
Если в области  выполнены условия теоремы Коши, то для нахождения частного решения (8.7.7) достаточно разрешить уравнения
выполнены условия теоремы Коши, то для нахождения частного решения (8.7.7) достаточно разрешить уравнения
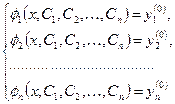 | (8.7.8) |
относительно 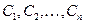 и подставить найденные значения постоянных в соотношения (8.7.6).
и подставить найденные значения постоянных в соотношения (8.7.6).
Одним из основных методов нахождения решения нормальных систем является метод исключения постоянных. С помощью этого метода данная система сводится к одному уравнению n–го порядка относительно одной неизвестной функции.
Пример
Найти общее решение системы уравнений 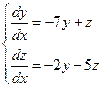
и выделить из него частное решение, удовлетворяющее начальным условиям 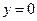 ,
, 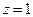 при
при 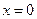 .
.
Решение
Продифференцировав первое из уравнений системы по 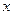 , получаем
, получаем 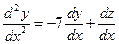 . Подставляя в это равенство выражение
. Подставляя в это равенство выражение 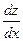 из второго уравнения системы и заменяя функцию
из второго уравнения системы и заменяя функцию 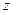 ее выражением из первого, приходим к линейному однородному уравнению второго порядка относительно одной неизвестной функции:
ее выражением из первого, приходим к линейному однородному уравнению второго порядка относительно одной неизвестной функции: 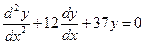 . Решив это уравнение, находим его общее решение
. Решив это уравнение, находим его общее решение 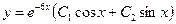 . Дифференцируя последнее равенство, имеем
. Дифференцируя последнее равенство, имеем 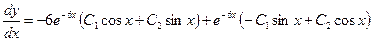 . Подставляя выражения для
. Подставляя выражения для 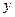 и
и 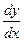 в первое уравнение системы и приводя подобные члены, получим
в первое уравнение системы и приводя подобные члены, получим 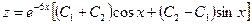 .
.
Окончательно, общее решение системы имеет вид
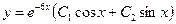 ,
, 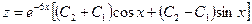 .
.
Решим теперь задачу Коши. Подставив в систему (*) вместо y, z и x их начальные значения 0, 1 и 0, получаем систему уравнений для определения постоянных 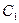 и
и 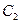 : 0=
: 0= 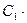 1+
1+ 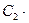 0, 1=(
0, 1=( 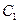 +
+ 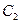 )
) 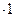 +(
+( 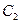 -
- 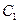 )
) 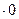 .
.
Отсюда 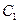 =0,
=0, 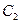 =1. Следовательно, искомым частным решением являются функции
=1. Следовательно, искомым частным решением являются функции 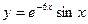 ,
, 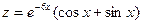 .
.
Если правые части нормальной системы (8.7.2) являются линейными функциями относительно неизвестных функций 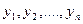 , то такая система называется линейной и имеет вид
, то такая система называется линейной и имеет вид
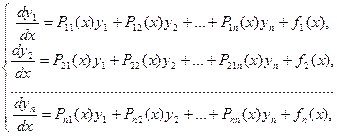 | (8.7.9) |
Если функции 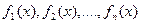 тождественно равны нулю, то линейная система называется однородной, в противном случае – неоднородной.
тождественно равны нулю, то линейная система называется однородной, в противном случае – неоднородной.
Системы линейных однородных диф. уравнений с постоянными коэффициентами
Рассмотрим систему трех уравнений с тремя неизвестными функциями x, e и z:
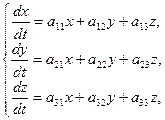 | (8.7.10) |
где 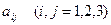 – вещественные числа, t – независимая переменная.
– вещественные числа, t – независимая переменная.
Будем искать частное решение системы (8.7.10) в следующем виде:
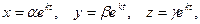 | (8.7.11) |
где a, b, g и k некоторые числа (причем 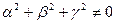 ), которые надо определить так, чтобы функции (8.7.11) были решением системы (8.7.10).
), которые надо определить так, чтобы функции (8.7.11) были решением системы (8.7.10).
Подставляя функции (8.7.11) и их производные в уравнения системы (8.7.10) и сокращая на 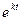 , получим
, получим
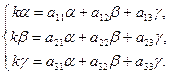
Перенося все члены в одну часть равенства и группируя коэффициенты при a, b, g получим систему уравнений
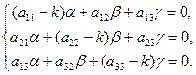 | (8.7.12) |
Система (8.7.12) – это однородная система трех уравнений первой степени с тремя неизвестными a, b и g. Как известно, чтобы эта система имела ненулевое решение, необходимо и достаточно, чтобы определитель был равен нулю, т.е. число k было корнем уравнения
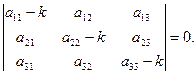 | (8.7.13) |
Уравнение (8.7.13) называют характеристическим уравнением для системы (8.7.10). Оно является уравнением третьей степени относительно k и имеет три корня: 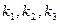 . Каждому корню соответствует ненулевое решение системы (8.7.12) (
. Каждому корню соответствует ненулевое решение системы (8.7.12) ( 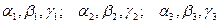 ), а следовательно, и частное решение данной системы (8.7.10):
), а следовательно, и частное решение данной системы (8.7.10):
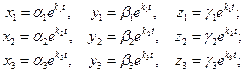
Если корни 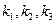 характеристического уравнения различны и вещественны, то общее решение системы (8.7.10) запишется в виде
характеристического уравнения различны и вещественны, то общее решение системы (8.7.10) запишется в виде
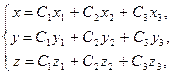 или или 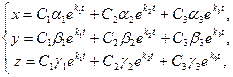 | (8.7.14) |
где 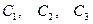 – произвольные постоянные.
– произвольные постоянные.
В случае, когда среди корней характеристического уравнения имеются кратные, корню 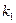 кратности r соответствует частное решение системы (8.7.10), имеющее вид
кратности r соответствует частное решение системы (8.7.10), имеющее вид
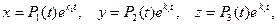 | (8.7.15) |
где 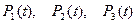 – многочлены степени не выше
– многочлены степени не выше 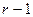 .
.
Пример
Найти общее решение системы 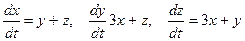 .
.
Решение
Ищем частное решение системы в виде 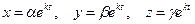 . Подставляя эти функции в систему, получаем
. Подставляя эти функции в систему, получаем
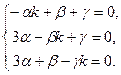 | (П.1) |
Составляем характеристическое уравнение 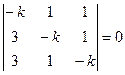 . Отсюда получаем уравнение
. Отсюда получаем уравнение 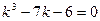 . Корни характеристического уравнения
. Корни характеристического уравнения 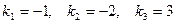 различны и вещественны.
различны и вещественны.
Найдем частное решение, соответствующее корню 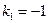 . Подставим его значение в систему (П.1). Полагая
. Подставим его значение в систему (П.1). Полагая 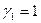 , находим
, находим 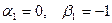 . Решение имеет вид
. Решение имеет вид 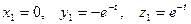 .
.
Аналогично для корня 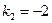 получаем
получаем 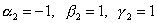 . Решение имеет вид
. Решение имеет вид 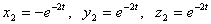 .
.
Третий корень 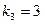 дает
дает 
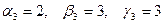 . Решение
. Решение 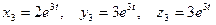 .
.
Общее решение системы имеет вид
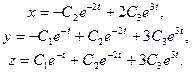
Пример
Найти общее решение системы 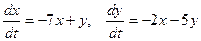
Решение
Ищем частное решение в виде 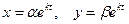 . При этом получаем характеристическое уравнение:
. При этом получаем характеристическое уравнение: 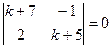 или
или 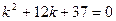 . Корни этого уравнения
. Корни этого уравнения 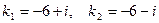 комплексно сопряженные. Для первого корня имеем
комплексно сопряженные. Для первого корня имеем 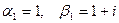 и, значит,
и, значит, 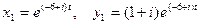 – решение данной системы.
– решение данной системы.
Аналогично для второго корня частное решение равно 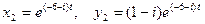 . Выделив из обоих частных решений вещественные части, получаем общее решение системы
. Выделив из обоих частных решений вещественные части, получаем общее решение системы
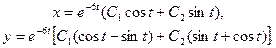
Пример
Найти общее решение системы
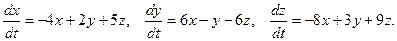 | (П.2) |
Решение
Характеристическое уравнение 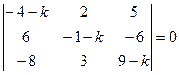 , или
, или 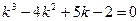 имеет корни
имеет корни 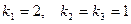
Найдем частное решение вида 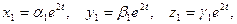 соответствующее корню
соответствующее корню 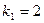 . Из системы имеем
. Из системы имеем 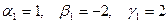 . Искомым частным решением являются функции
. Искомым частным решением являются функции 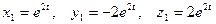 .
.
Теперь найдем два частных решения, соответствующих кратному корню 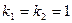 .
.
Согласно (8.7.15), ему отвечает решение вида
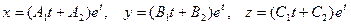 | (П.3) |
Коэффициенты 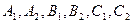 определяются подстановкой (П.3) в систему (П.2). Выбрав в качестве произвольных коэффициенты
определяются подстановкой (П.3) в систему (П.2). Выбрав в качестве произвольных коэффициенты 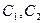 , найдем
, найдем 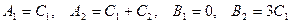 . Решения (П.3) принимают вид
. Решения (П.3) принимают вид 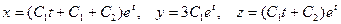 .
.
Полагая сначала 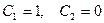 , а затем
, а затем 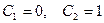 , находим два частных решения, соответствующих кратному корню
, находим два частных решения, соответствующих кратному корню 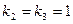 :
: 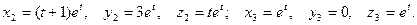
И, наконец, общим решением данной системы являются функции
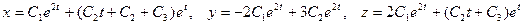 .
.
Упражнения
Проинтегрировать следующие уравнения различных типов:
| 1. | 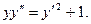 | 2. | 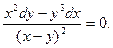 |
| 3. | 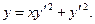 | 4. | 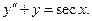 |
| 5. | 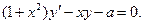 | 6. | 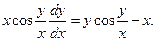 |
| 7. | 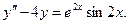 | 8. | 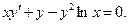 |
| 9. | 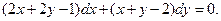 | 10. | 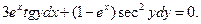 |
Проинтегрировать следующие системы .уравнений:
| 11. | 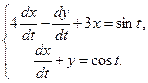 | 12. | 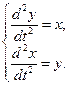 |
| 13. | 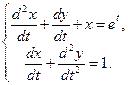 | 14. | 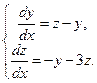 |
Глава 9. Ряды
Основные понятия. Сходимость ряда
Определение: Рассмотрим числовую последовательность 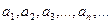 . Образуем из элементов этой последовательности выражение вида
. Образуем из элементов этой последовательности выражение вида
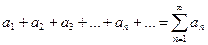 , , | (9.1.1) |
которое называется числовым рядом, или просто рядом. Слагаемые в формуле (9.1.1) называются членами ряда. Суммы первых n членов ряда называются частичными суммами ряда:
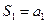 , , 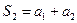 , …, , …, 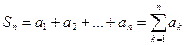 | (9.1.2) |
Поскольку число членов ряда бесконечно, то частичные суммы ряда образуют числовую последовательность 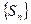 :
:
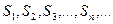 . . | (9.1.3) |
Ряд (9.1.1) называется сходящимся, если существует предел S последовательности частичных сумм (9.1.3); в таком случае число S называется суммой ряда:
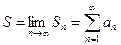 | (9.1.4) |
Если же последовательность частичных сумм (9.1.3) не имеет предела, числовой ряд (9.1.1) называется расходящимся.
Рассмотрим примеры числовых рядов.
1. Дан ряд 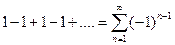 . Последовательность частичных сумм этого ряда
. Последовательность частичных сумм этого ряда 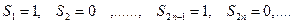 не имеет предела, т.е. ряд расходится.
не имеет предела, т.е. ряд расходится.
2. Дан ряд составленный из элементов геометрической прогрессии с первым членом 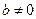 и знаменателем
и знаменателем 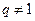 :
: 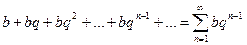 .
.
Частичная сумма этого ряда выражается формулой 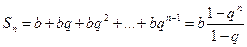 .
.
1. При |q|< 1 пределом является число 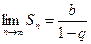 , которое также будет и суммой данного ряда.
, которое также будет и суммой данного ряда.
2. При |q|> 1 предел 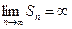 и ряд расходится.
и ряд расходится.
3. Если же |q|= 1, то данный ряд также расходится.
