Оценка качества модели в целом.

АЛГОРИТМ РЕШЕНИЯ И ПОЯСНЕНИЕ К РЕШЕНИЮ ЗАДАЧИ КОНТРОЛЬНОЙ РАБОТЫ

Расчет параметров линейной множественной регрессии.

Для расчета параметров используем метод наименьших квадратов.

В рамках данного метода составляют систему нормальных уравнений:

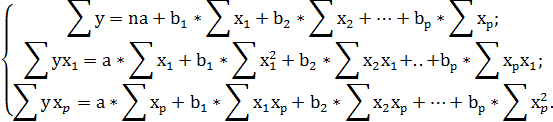
Неизвестными величинами в данной системе являются искомые параметры ( 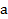, , 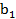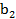). Суммы – определяются на основании исходного массива наблюдений. Для удобства определения искомых сумм составляют таблицу вспомогательных расчетов. Макет данной таблицы приведен ниже.

Таблица – Вспомогательные расчеты

№	y	x1	x2	x12	x22	y2	x1x2	yx1	yx2
сумма8
среднее значение88

^* - сумма определяется путем суммирования всех строк по соответствующему столбцу;

^** - среднее значение находится как среднее арифметическое простое.

Далее записывается уравнение множественной регрессии с полученными параметрами:

Например, 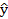=1,84+0,95х₁+0,086х₂.

Параметр а – свободный член уравнения - экономической интерпретации не имеет. Параметры b_i, называемые коэффициентами чистой регрессии, показывают, как изменится зависимая переменная у при изменении соответствующего фактора х на одну единицу при элиминировании влияния других факторов.

Например, если использовать пример уравнения множественной регрессии, приведенный выше, то вывод по коэффициентам чистой регрессии выглядит следующим образом:

С увеличением ввода в действие новых основных фондов на 1 % выработка продукции на одного работника возрастет на 0,95 тыс. руб. при фиксированном значении фактора удельного веса рабочих высокой квалификации в общей численности рабочих.

С увеличением удельного веса рабочих высокой квалификации в общей численности рабочих на 1 % выработка продукции на одного работника возрастет на 0,086 тыс. руб. при фиксированном значении фактора ввода в действие новых основных фондов.

Оценка качества модели в целом.

Для оценки качества модели регрессии используют критерий Фишера.

Расчетное значение данного критерия составит:

F= ,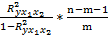

где 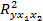– коэффициент множественной детерминации;

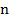– количество наблюдений;

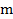– количество зависимых переменных в модели.

Коэффициент множественной детерминации определяем по следующей формуле:

.

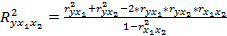Произведем расчет парных коэффициентов корреляции:

r_ух= ;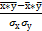

где 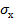и - среднеквадратические отклонения по соответствующим признакам:

,

.

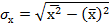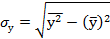Для расчета используются цифры из таблицы вспомогательных расчетов (см. последние строки таблицы).

Парные коэффициенты корреляции принимают значения .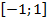

Коэффициент детерминации - 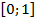и показывает, какая часть дисперсии результативного признака объяснена уравнением регрессии.

Например, 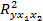= 0,94. Вывод: коэффициент множественной детерминации показывает, что 94 % вариации выработки продукции на одного работника зависит от рассматриваемых факторов в модели. На долю прочих факторов, не учтенных в модели, приходится 6 %.

Далее определяют расчетное и табличное значение критерия Фишера (формулу расчетного значения данного критерия см. выше).

Табличное значение данного критерия для данной задачи при уровне значимости 0,05 и степенях свободы k₁=m=2 и k₂=n-m-1=17 составит 3,59.

Анализируя полученные результаты можно сделать вывод, что в случае, если расчетного значение критерия Фишера превышает табличное, то уравнение множественной регрессии статистически надежно.

3. Оценка целесообразности включения в модель фактора х₁ после х₂ и х₂ после х₁.

Для оценки целесообразности включения в модель фактора х₁ после х₂ производят расчет частного критерия Фишера.

Расчетное значение данного критерия составит:

.

.

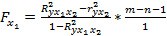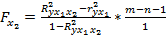где 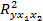– коэффициент множественной детерминации;

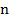– количество наблюдений;

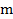– количество зависимых переменных в модели;

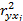– парные коэффициенты детерминации ( ).

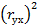Табличное значение данного критерия для данной задачи при уровне значимости 0,05 и степенях свободы k₁=1 и k₂=n-m-1=17 составит 4,45.

По наибольшему значению данного критерия судят о целесообразности введения в модель соответствующего фактора. А также о статистической надежности данного фактора для модели. В случае, когда расчетное значение критерия по соответствующему фактору превышает табличное, то это свидетельствует о статистической значимости соответствующего фактора для регрессионной модели.