Метод кубической интерполяции
Постановка задачи
Требуется найти безусловный минимум функции f(x) одной переменной, т.е. такую точку 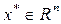 , что
, что 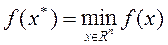 .
.
Стратегия поиска
Задается начальная точка и с помощью серии пробных шагов находятся две точки, первые производные в которых имеют противоположные знаки. По величине функции и ее первых производных в полученных точках строится интерполяционный полином третьей степени. В качестве приближения точки минимума берется точка минимума полинома. Процесс поиска заканчивается, если производная в точке минимума полинома достаточно мала или процедура становится неэффективной.
Алгоритм
Шаг 1. Задать начальную точку х0,величину шага 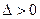 и малые положительные числа
и малые положительные числа 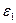 и
и 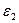 .
.
Шаг 2. Вычислить производную 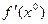 .
.
Шаг 3. Проверить знак производной в точке х0:
а) если 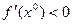 , вычислить
, вычислить 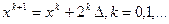 , вплоть до точки хM, в которой
, вплоть до точки хM, в которой 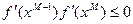 ;
;
б) если 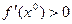 , вычислить
, вычислить 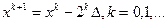 , вплоть до точки хM, в которой
, вплоть до точки хM, в которой 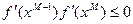 .
.
Шаг 4. Положить 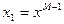 ,
, 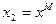 и вычислить
и вычислить 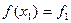 ,
, 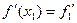 ,
, 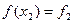 ,
, 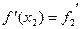 .
.
Шаг 5. Найти точку минимума кубического интерполяционного полинома по формуле
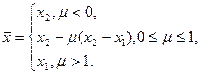 ,
,
где 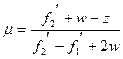 ,
, 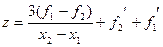 ,
, 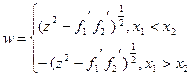
и значение 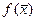 .
.
Шаг 6. Проверить условие убывания:
а) если 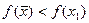 , перейти к шагу 7;
, перейти к шагу 7;
б) если 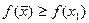 , вычислять
, вычислять 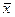 по формуле
по формуле 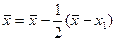 до тех пор,
до тех пор,
пока не будет выполнено неравенство 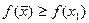 .
.
7. Проверить выполнение условий окончания:
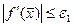 ,
, 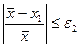 :
:
а) если оба условия выполнены, процедура закончена и 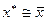 ;
;
б) если хотя бы одно из условий не выполнено, положить либо 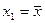 ,
, 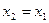 , если
, если 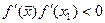 , либо
, либо 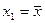 ,
, 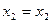 , если
, если 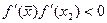 . Перейти к шагу 5.
. Перейти к шагу 5.
Замечания.
1. На шагах 2 и 3 реализуется эвристическая процедура поиска границ интервала неопределенности, где изменение знака производной свидетельствует о переходе через точку минимума.
2. Формула, используемая на шаге 5, гарантирует, что точка 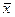 не выйдет за границы интервала [х1,х2].
не выйдет за границы интервала [х1,х2].
3. На шаге 6 проверяется, действительно ли точка 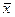 является приближением к минимуму.
является приближением к минимуму.
4. На шаге 7 из трех точек х1, х2, 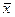 выбираются две, в которых знаки первых производных различны, после чего процедура кубической интерполяции повторяется.
выбираются две, в которых знаки первых производных различны, после чего процедура кубической интерполяции повторяется.
5. Интерполяционный полином третьей степени строится по двум точкам вместо обычных четырех, так как в каждой точке используется информация о производной.
Пример 6.7.Найти минимум функции 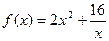 методом кубической интерполяции.
методом кубической интерполяции.
1. Зададим х0=1; 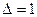 ;
; 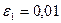 ;
; 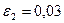 .
.
2. Вычислим 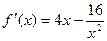 ;
; 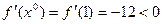 .
.
3. Так как 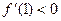 , то
, то 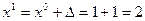 . Вычислим
. Вычислим 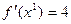 . Поэтому
. Поэтому 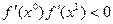 , M = 1.
, M = 1.
40.Положим 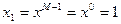 ,
, 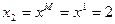 и вычислим
и вычислим
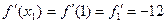 ;
; 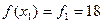 ;
;
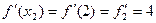 ;
; 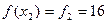
50. Вычислим
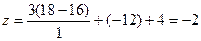 ;
; 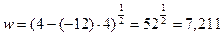 ;
;
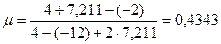 ;
; 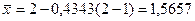 ;
; 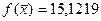 .
.
60. Проверим условие убывания. Так как 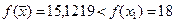 , то переходим к шагу 7.
, то переходим к шагу 7.
70. Проверим условие окончания: 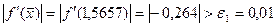 . Условие не выполняется. Так как справедливо
. Условие не выполняется. Так как справедливо 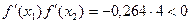 , то
, то 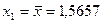 ;
; 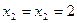 . Переходим к шагу 5.
. Переходим к шагу 5.
51. Вычислим 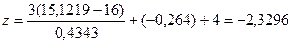 ,
, 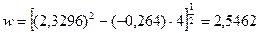 ;
; 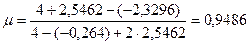 ;
; 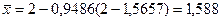 ;
; 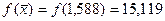 .
.
61. Проверим условие убывания. Так как 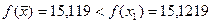 , то переходим к шагу 7.
, то переходим к шагу 7.
71. Проверим условия окончания: 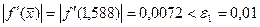 (выполняется) и
(выполняется) и 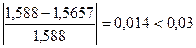 (выполняется). Поэтому расчет окончен и
(выполняется). Поэтому расчет окончен и 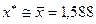 . Точная координата точки минимума
. Точная координата точки минимума 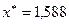 , откуда следует, что применение кубической интерполяции даёт лучший результат, чем применение квадратичной интерполяции.
, откуда следует, что применение кубической интерполяции даёт лучший результат, чем применение квадратичной интерполяции.
Варианты заданий. Таблица 1.
| № варианта | Метод сканирования | Метод половинного деления | Метод золотого сечения | Метод кубической интерполяции |
Для функции: R(x)=DSin(Ax+C) найти максимум на следующем интервале: x 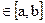 | Найти безусловный минимум функции f(x) одной переменной, т.е. такую точку 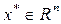 , что , что 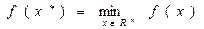 . . | |||
| 1. |  = =  А=1,0; В=1,0; С=1,0; D=1,0. Ошибка задается по х: ε =0,04 А=1,0; В=1,0; С=1,0; D=1,0. Ошибка задается по х: ε =0,04 |  = =  А=1,0; В=1,0; С=1,0; D=1,0. Ошибка задается по х: ε =0,04 А=1,0; В=1,0; С=1,0; D=1,0. Ошибка задается по х: ε =0,04 |  = =  А=1,0; В=1,0; С=1,0; D=1,0. Ошибка задается по х: ε =0,04 А=1,0; В=1,0; С=1,0; D=1,0. Ошибка задается по х: ε =0,04 | Найти минимум функции 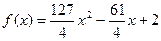 х0=1; х0=1; 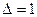 ; ; 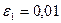 ; ; 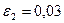 . . |
| 2. |  = =  А=1,0; В=2,0; С=1,0; D=1,0. Ошибка задается по х: ε =0,05 А=1,0; В=2,0; С=1,0; D=1,0. Ошибка задается по х: ε =0,05 |  = =  А=1,0; В=2,0; С=1,0; D=1,0. Ошибка задается по х: ε =0,05 А=1,0; В=2,0; С=1,0; D=1,0. Ошибка задается по х: ε =0,05 |  = =  А=1,0; В=2,0; С=1,0; D=1,0. Ошибка задается по х: ε =0,05 А=1,0; В=2,0; С=1,0; D=1,0. Ошибка задается по х: ε =0,05 | Найти минимум функции 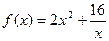 х0=0,5; х0=0,5; 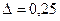 ; ; 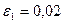 ; ; 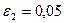 . . |
| 3. |  = =  А=2,0; В=1,0; С=1,0; D=1,0. Ошибка задается по х: ε =0,04 А=2,0; В=1,0; С=1,0; D=1,0. Ошибка задается по х: ε =0,04 |  = =  А=2,0; В=1,0; С=1,0; D=1,0. Ошибка задается по х: ε =0,04 А=2,0; В=1,0; С=1,0; D=1,0. Ошибка задается по х: ε =0,04 |  = =  А=2,0; В=1,0; С=1,0; D=1,0. Ошибка задается по х: ε =0,04 А=2,0; В=1,0; С=1,0; D=1,0. Ошибка задается по х: ε =0,04 | Найти минимум функции 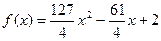 х0=0,5; х0=0,5; 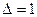 ; ; 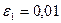 ; ; 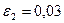 . . |
| 4. |  = =  А=1,0; В=1,0; С=2,0; D=2,0. Ошибка задается по х: ε =0,05 А=1,0; В=1,0; С=2,0; D=2,0. Ошибка задается по х: ε =0,05 |  = =  А=1,0; В=1,0; С=2,0; D=2,0. Ошибка задается по х: ε =0,05 А=1,0; В=1,0; С=2,0; D=2,0. Ошибка задается по х: ε =0,05 |  = =  А=1,0; В=1,0; С=2,0; D=2,0. Ошибка задается по х: ε =0,05 А=1,0; В=1,0; С=2,0; D=2,0. Ошибка задается по х: ε =0,05 | Найти минимум функции 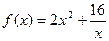 х0=1; х0=1; 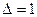 ; ; 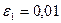 ; ; 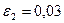 . . |
| 5. |  = =  А=2,0; В=2,0; С=1,0; D=1,0. Ошибка задается по х: ε =0,04 А=2,0; В=2,0; С=1,0; D=1,0. Ошибка задается по х: ε =0,04 |  = =  А=2,0; В=2,0; С=1,0; D=1,0. Ошибка задается по х: ε ε =0,04 А=2,0; В=2,0; С=1,0; D=1,0. Ошибка задается по х: ε ε =0,04 |  = =  А=2,0; В=2,0; С=1,0; D=1,0. Ошибка задается по х: ε =0,04 А=2,0; В=2,0; С=1,0; D=1,0. Ошибка задается по х: ε =0,04 | Найти минимум функции 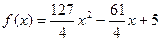 х0=1; х0=1; 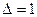 ; ; 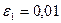 ; ; 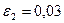 . . |
| 6. |  = =  А=1,0; В=1,0; С=2,0; D=2,0. Ошибка задается по х: ε =0,04 А=1,0; В=1,0; С=2,0; D=2,0. Ошибка задается по х: ε =0,04 |  = =  А=1,0; В=1,0; С=2,0; D=2,0. Ошибка задается по х: ε =0,04 А=1,0; В=1,0; С=2,0; D=2,0. Ошибка задается по х: ε =0,04 |  = =  А=1,0; В=1,0; С=2,0; D=2,0. Ошибка задается по х: ε =0,04 А=1,0; В=1,0; С=2,0; D=2,0. Ошибка задается по х: ε =0,04 | Найти минимум функции 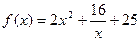 х0=0,5; х0=0,5; 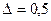 ; ; 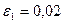 ; ; 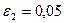 . . |
| Продолжение таблицы 1. | ||||
| 7. |  = =  А=1,0; В=2,0; С=1,0; D=2,0. Ошибка задается по х: ε =0,04 А=1,0; В=2,0; С=1,0; D=2,0. Ошибка задается по х: ε =0,04 |  = =  А=1,0; В=2,0; С=1,0; D=2,0. Ошибка задается по х: ε =0,04 А=1,0; В=2,0; С=1,0; D=2,0. Ошибка задается по х: ε =0,04 |  = =  А=1,0; В=2,0; С=1,0; D=2,0. Ошибка задается по х: ε =0,04 А=1,0; В=2,0; С=1,0; D=2,0. Ошибка задается по х: ε =0,04 | Найти минимум функции 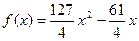 х0=1; х0=1; 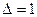 ; ; 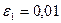 ; ; 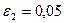 . . |
| 8. |  = =  А=2,0; В=1,0; С=2,0; D=1,0. Ошибка задается по х: ε =0,04 А=2,0; В=1,0; С=2,0; D=1,0. Ошибка задается по х: ε =0,04 |  = =  А=2,0; В=1,0; С=2,0; D=1,0. Ошибка задается по х: ε =0,04 А=2,0; В=1,0; С=2,0; D=1,0. Ошибка задается по х: ε =0,04 |  = =  А=2,0; В=1,0; С=2,0; D=1,0. Ошибка задается по х: ε =0,04 А=2,0; В=1,0; С=2,0; D=1,0. Ошибка задается по х: ε =0,04 | Найти минимум функции 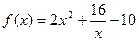 х0=1; х0=1; 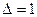 ; ; 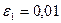 ; ; 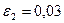 . . |
| 9. |  = =  А=3,0; В=1,0; С=2,0; D=1,0. Ошибка задается по х: ε =0,05 А=3,0; В=1,0; С=2,0; D=1,0. Ошибка задается по х: ε =0,05 |  = =  А=3,0; В=1,0; С=2,0; D=1,0. Ошибка задается по х: ε =0,05 А=3,0; В=1,0; С=2,0; D=1,0. Ошибка задается по х: ε =0,05 |  = =  А=3,0; В=1,0; С=2,0; D=1,0. Ошибка задается по х: ε =0,05 А=3,0; В=1,0; С=2,0; D=1,0. Ошибка задается по х: ε =0,05 | Найти минимум функции 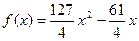 х0=1; х0=1; 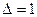 ; ; 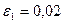 ; ; 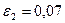 . . |
| 10. |  = =  А=4,0; В=1,0; С=1,0; D=2,0. Ошибка задается по х: ε =0,05 А=4,0; В=1,0; С=1,0; D=2,0. Ошибка задается по х: ε =0,05 |  = =  А=4,0; В=1,0; С=1,0; D=2,0. Ошибка задается по х: ε =0,05 А=4,0; В=1,0; С=1,0; D=2,0. Ошибка задается по х: ε =0,05 |  = =  А=4,0; В=1,0; С=1,0; D=2,0. Ошибка задается по х: ε =0,05 А=4,0; В=1,0; С=1,0; D=2,0. Ошибка задается по х: ε =0,05 | Найти минимум функции 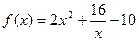 х0=1; х0=1; 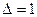 ; ; 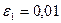 ; ; 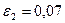 . . |
