Обработка результатов эксперимента. Местный коэффициент теплоотдачи от поверхности опытной трубы к воздуху определяется соотношением:

Местный коэффициент теплоотдачи от поверхности опытной трубы к воздуху определяется соотношением:

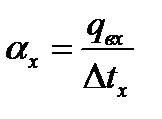(3.1)

где 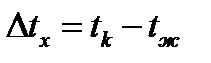- разность температур трубы и воздуха.

Конвективная составляющая плотности теплового потока выражается разностью полной плотности теплового потока и плотности теплового потока излучения:

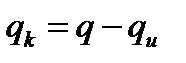(3.2)

Полная плотность теплового потока вычисляется по формуле:

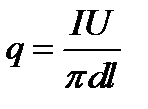(3.3)

где I, U - показания амперметра и вольтметра;

d=0,008 м – наружный диаметр трубы;

l=1,3 м – длина обогреваемого участка трубы.

Лучистую составляющую плотности теплового потока находят расчетным путем:

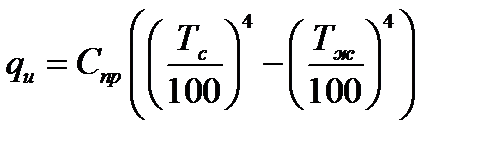(3.4)

где 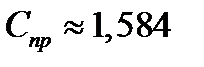Вт/(м²∙К²); 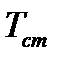, 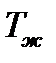- температуры трубы и среды, К.

По полученным значениям местных коэффициентов теплоотдачи строят график 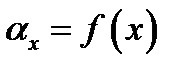. Здесь же строят график температуры трубы по высоте 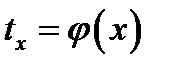. Далее опытные данные необходимо привести к безразмерному виду, вычислив:

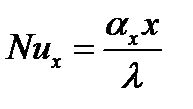(3.5)

и

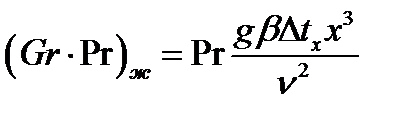(3.6)

Затем полученные результаты представляют в виде графика зависимости:

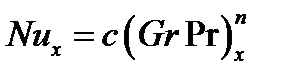(3.7)

выполненного в логарифмических координатах.

3.7 Указания ксоставлению отчета

Отчет о выполненной работе должен содержать: принципиальную схему экспериментального стенда; протокол испытаний; обработку результатов опытов, оценку погрешности, графики: , , .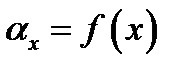

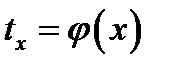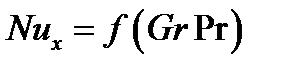Вопросы для самопроверки

1. Что такое естественная конвекция?

2. Физическая природа процесса теплоотдачи при свободной конвекции.

3. Закон Ньютона-Рихмана для конвективной теплопередачи.

4. Закон Ньютона-Рихмана для местной теплоотдачи.

5. Характер изменения температуры поверхности и местного коэффициента теплоотдачи по высоте трубы; режимы движения воздуха в пограничном слое, определение точки перехода.

6. Обобщение опытных данных с применением теории подобия.

7. Изобразите траектории свободного движения воздуха около горячей вертикальной трубы.

8. Что называется конвективным теплообменом? Какие различают виды конвекции?

9. Вследствие чего возникает естественная конвекция?

10. Какими числами подобия характеризуется конвективный теплообмен?

11. Особенности теплоотдачи капельных жидкостей по сравнению с теплоотдачей газов.

12. Гидродинамический и тепловой пограничный слой.

13. Опишите устройство и принцип работы установки.

14. Зачем в схему установки включен трансформатор?

ПРОТОКОЛ

Исследование теплоотдачи при естественной конвекции газа около горизонтальной трубы

«» 20 г.

Температура окружающего воздуха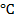

Сила тока через трубу А.

Падение напряжения на трубеВ.

Координата x, мм
tx,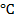
qu, Вт/м2
qk, Вт/м2
αx, Вт/м2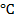
(GrPr)
Nux
ln(GrPr)
lnNu

4 Методические указания к лабораторной работе №4 «Кипение жидкости на обогреваемой поверхности»

Цель работы

4.1.1. Целью работы является расширение и углубление знаний о механизме кипения жидкости на обогреваемой поверхности.

4.1.2. Во время подготовки и выполнения работы студенты должны изучить опытную установку, освоить методику проведения экспериментов, составления протокола и обработки результатов.

Основы теории

4.2.1 В теплообменных аппаратах энергетических и теплотехнологических установок происходят процессы образования пара за счёт подвода теплоты от высокотемпературных источников (паровые котлы, паропреобразователи и др. установки).

На рисунке 6 показан сосуд с кипящей водой и паром и график изменения температуры по высоте воды и пара. Как следует из графика, жидкость оказывается несколько перегретой в сравнении с температурой пара.

Интенсивность теплообмена между днищем и водой в значительной степени зависит от температурного режима, кипение при этом может быть пузырьковое и плёночное.

Удельный тепловой поток при кипении жидкости определяется по уравнению Ньютона-Рихмана:

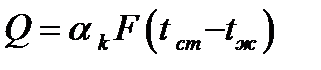(4.1)

где 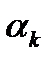- коэффициент теплоотдачи при кипении жидкости;

F – поверхность теплообмена;

t_ст – температура нагретой стенки;

t_ж – температура потока жидкости.

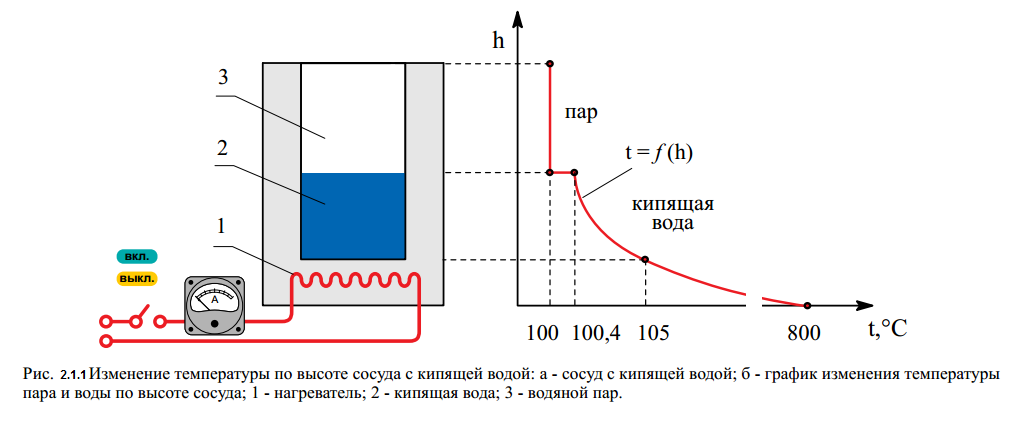
1 – нагреватель, 2 – кипящая вода, 3 – водяной пар

Рисунок 6 – Изменение температуры по высоте сосуда с кипящей водой

Различают объемное и поверхностное кипение. Объемное кипение – образование паровых пузырей внутри массы жидкости, находящейся в перегретом, или метастабильном, состоянии при Т_ж>Т_кип, где Т_ж – температура перегретой жидкости. Такое кипение реализуется в так называемых аппаратах объемного вскипания, эффективных для обезвреживания и утилизации агрессивных жидкостей.

Поверхностное кипение – парообразование на поверхности нагрева, имеющей температуру Т_н>Т_кип. Такое кипение возможно и в случае, когда температура основной массы жидкости Т_ж<Т_кип, но в окрестности поверхности нагрева образовался пограничный слой, перегретый до температуры, превышающей Т_кип. Основные виды поверхностного кипения – пузырьковое и пленочное.

Пузырьковое кипение возникает при умеренных тепловых потоках на микровпадинах поверхности, смачиваемой жидкостью. Пар генерируется на действующих центрах парообразования в виде цепочек пузырей.

Пленочное кипение возникает на несмачиваемых поверхностях нагрева (например, кипение ртути в стеклянной трубке); на смачиваемых поверхностях пузырьковое кипение переходит в пленочное (первый кризис кипения) при достижении первой критической плотности теплового потока 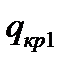. Интенсивность теплоотдачи при пленочном кипении значительно меньше, чем при пузырьковом, что обусловлено малыми значениями коэффициента теплопроводности 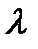[Вт/(мК)] и плотности пара по сравнению с их значениями для жидкости. Повышение давления приводит к возрастанию 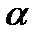в обоих случаях. Разрушение пленочного кипения и восстановление пузырькового (второй кризис кипения) на смачиваемых поверхностях происходит при второй критической плотности теплового потока (рисунок 7).

Кризисы кипения определяются преимущественно гидродинамическим механизмом потери устойчивости структуры пристенного двухфазного пограничного слоя. Критерий гидродинамической устойчивости кипения имеет вид:

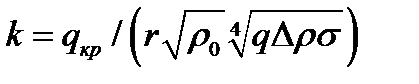(4.2)

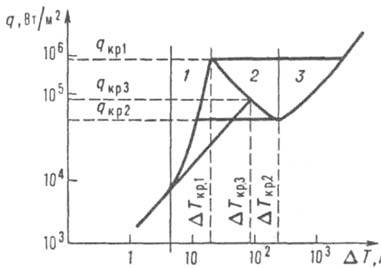
1 – пузырьковый режим; 2 – переходный режим, характеризуемый сменой пузырьковой структуры на поверхности нагрева сплошным паровым слоем (пленкой), от которого отрываются крупные паровые пузыри; 3 – пленочный режим

Рисунок 7 – Зависимость плотности теплового потока от разности температур

При низких давлениях возможен третий кризис кипения в форме непосредственного перехода от режима конвективного движения жидкости к развитому пленочному кипению. Этот переход имеет цепной кавитационный механизм и реализуется при разностях температур на поверхности нагрева и кипение, удовлетворяющих условию:

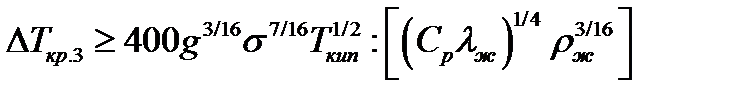(4.3)

4.2.2 При небольшой 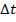капля жидкости расплывается по поверхности и внутри жидкости идет образование отдельных пузырьков пара, уходящих через свободную поверхность капли. На сильно нагретой поверхности опущенная на нее навеска жидкости собирается в каплю приблизительно сферической формы, отделенную от твердой поверхности и находящуюся в непрерывном движении. В последнем случае время испарения капли во много раз больше времени испарения при пузырьковом кипении, что объясняется резким ухудшением теплоотдачи при высоких значениях разности температур 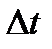. Это явление носит название кризиса кипения.

Рассмотрим процесс испарения капли в соответствии упрощенной схемой явления, изображенной на рисунке 8.

R(τ)

ts

tw

q

Рисунок 8 – Принципиальная схема лабораторной установки

Пусть на обогреваемую поверхность помещена капля начального радиуса R₀. По истечении времени τ вследствие непрерывного подвода тепла радиус сферической капли уменьшится до размера R(τ). Будем считать, что температура жидкости в течение всего опыта равна 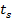, а разность температур 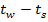и тепловой поток q постоянны.

Уравнение баланса тепла за промежуток времени dτ:

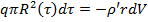(4.4)

где dV — уменьшение объема капли за время dτ;

ρ' и r – плотность и скрытая теплота парообразования воды при атмосферном давлении.

2.3 Левая часть уравнения (4.4) соответствует количеству тепла, поступившего в каплю через площадь проекции ее на поверхность за время dτ, правая часть выражает собой количество тепла, унесенное испарившейся порцией воды, в результате чего объем капли уменьшился на величину:

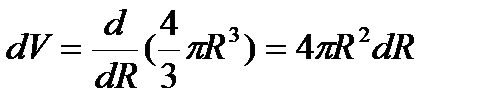(4.5)

Подстановка (4.5) в(4.4) , после сокращения и интегрирования приводит:

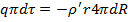(4.6)

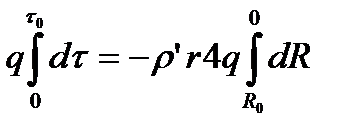(4.7)

где 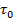– время испарения капли с начальным радиусом 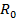, соответствующим начальному объему .

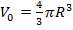Из выражения (4.7) найдем связь между q, , :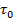

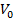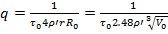(4.8)

С другой стороны по определению коэффициента теплоотдачи α:

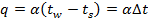(4.9)

Сопоставляя 4.8 и 4.9 получим связь между α и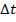

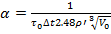(4.10)

Таким образом, варьируя величину 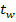и измеряя в каждом опыте 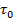и 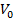по формуле (4.10), можно построить зависимость:

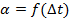(4.11)

а так же

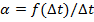(4.12)

4.2.4 При опытном исследовании сравнительно легко могут быть определены начальный объем капли 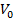(при помощи калибровочной капельницы или шприца), время испарения капли 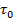и более грубо температура поверхности - .

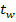Описанная ниже экспериментальная установка позволяет в каждом эксперименте фиксировать 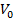, , 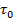и 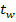.