Наибольший общий делитель (НОД ( ))
Класс
«Целочисленность и делимость»
Основная теорема арифметики. Всякое натуральное число единственным образом раскладывается в произведение степеней простых чисел: 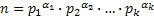 . (Простым называется число, которое не имеет других делителей, кроме 1 и самого себя).
. (Простым называется число, которое не имеет других делителей, кроме 1 и самого себя).
Теорема 1. Количество делителей числа 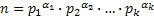 , включая 1 и само число, равно
, включая 1 и само число, равно 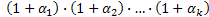 .
.
Пример 1. (Задание С6 ЕГЭ 2010). Найдите все натуральные числа, последняя десятичная цифра которых 0 и которые имеют ровно 15 различных натуральных делителей (включая единицу и само число).
Решение:Ищем числа вида 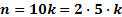 .Воспользуемся теоремой 1 . Из этой теоремы следует, что число различных делителей числа 10 равно 4. Если в разложении числа
.Воспользуемся теоремой 1 . Из этой теоремы следует, что число различных делителей числа 10 равно 4. Если в разложении числа 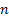 на простые множители появится еще 1 сомножитель, кроме 2 и 5, то число делителей будет кратным 4, но число 15 (как количество делителей) не делится на 4. Поэтому других делителей нет, т.е. число
на простые множители появится еще 1 сомножитель, кроме 2 и 5, то число делителей будет кратным 4, но число 15 (как количество делителей) не делится на 4. Поэтому других делителей нет, т.е. число 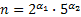 , а количество делителей равно
, а количество делителей равно 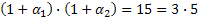 . Отсюда
. Отсюда 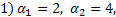 или 2)
или 2) 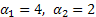
 Тогда искомыми будут числа: 1)
Тогда искомыми будут числа: 1) 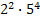 и
и 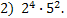
Ответ: 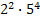 и
и 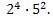
Деление с остатком.
Если при делении числа 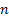 на число
на число 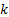 получается остаток
получается остаток 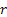 , то
, то 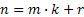 , где
, где 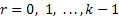 или
или
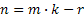 , где
, где 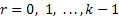 .
.
Сравнение чисел по модулю 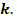
Определение. Говорят, что число 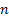 равно числу
равно числу 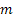 по модулю
по модулю 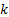 :
:
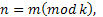 если разность этих чисел делится на
если разность этих чисел делится на 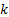 , т.е. когда эти числа имеют одинаковый остаток при делении на
, т.е. когда эти числа имеют одинаковый остаток при делении на 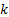 .
.
Заметим, что если число 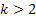 , то удобно использовать и отрицательные остатки. Например,
, то удобно использовать и отрицательные остатки. Например, 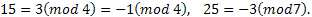
Теорема 2. Если 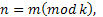 то
то 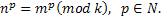
Пример 2. На какую цифру оканчивается разность 92009 – 72010 ?
Решение: 90 оканчивается на 1 , 91 оканчивается на 9 , 92 снова оканчивается на 1 , и так далее. Так как 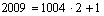 , то 92009 оканчивается на 9 . Далее, 70 оканчивается на 1 , 71 оканчивается на 7 , 72 оканчивается на 9 , 73 оканчивается на 3, 74 снова оканчивается на 1 , и так далее. А так как
, то 92009 оканчивается на 9 . Далее, 70 оканчивается на 1 , 71 оканчивается на 7 , 72 оканчивается на 9 , 73 оканчивается на 3, 74 снова оканчивается на 1 , и так далее. А так как 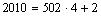 , то 72010 оканчивается на 9 . Поэтому разность 92009 – 72010 оканчивается на 0 .
, то 72010 оканчивается на 9 . Поэтому разность 92009 – 72010 оканчивается на 0 .
Другое решение: (С использованием Теоремы 2). Определить, на какую цифру оканчивается число, означает – найти остаток при делении этого числа на 10. 
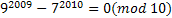 .
.
Ответ: на 0.
Пример 3.Покажите, что если m и n - целые числа, а m2 + n2 делится на 3 , то m и n оба делятся на 3 .
Решение: заметим, что числа 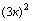 ,
, 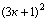 и
и 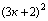 дают при делении на 3 дают остатки соответственно 0 , 1 и 1 . Поэтому m2 + n2 делится на 3 тогда и только тогда, когда m и n оба делятся на 3 .
дают при делении на 3 дают остатки соответственно 0 , 1 и 1 . Поэтому m2 + n2 делится на 3 тогда и только тогда, когда m и n оба делятся на 3 .
Пример 4.(Задание С6 ЕГЭ 2010). Решите уравнение 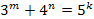
в натуральных числах.
Решение:Одно решение угадывается сразу: 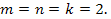 Далее, при делениина 4 число 3 дает в остатке (-1), а число 5 дает в остатке 1, следовательно, правая часть равенства при делениина 4 дает в остатке
Далее, при делениина 4 число 3 дает в остатке (-1), а число 5 дает в остатке 1, следовательно, правая часть равенства при делениина 4 дает в остатке 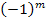 , а правая часть дает в остатке 1. Отсюда следует, что число
, а правая часть дает в остатке 1. Отсюда следует, что число 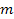 - четное, т.е.
- четное, т.е. 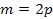 . Тогда уравнение перепишется в виде
. Тогда уравнение перепишется в виде 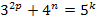 . Правая часть равенства при делениина 3 дает в остатке 1, а правая часть дает в остатке
. Правая часть равенства при делениина 3 дает в остатке 1, а правая часть дает в остатке 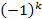 . Отсюда следует, что число k - четное, т.е.
. Отсюда следует, что число k - четное, т.е. 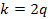 ( p и q теперь больше 1). Уравнение примет вид:
( p и q теперь больше 1). Уравнение примет вид: 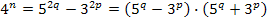 . Тогда
. Тогда 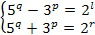 . Откуда
. Откуда  что дает уже угаданное решение. Если же
что дает уже угаданное решение. Если же 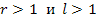 , то система не имеет решений, т.к. в левой части первого уравнения стоит нечетное число, а в правой – четное.
, то система не имеет решений, т.к. в левой части первого уравнения стоит нечетное число, а в правой – четное.
Ответ: 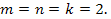
Наибольший общий делитель (НОД ( )).
Если числа разложены в произведение степеней простых чисел, то НОД равен произведению общих простых делителей в наименьших, входящих в них степеней. Этот способ не годится для нахождения НОД буквенных выражений. В этом случае удобно применить другой алгоритм (алгоритм Евклида), который основан на следующем свойстве:
