Отношение бесконечно больших
Докажем теорему для неопределённостей вида  .
.
Пусть, для начала, предел отношения производных конечен и равен 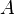 . Тогда, при стремлении
. Тогда, при стремлении 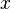 к
к 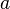 справа, это отношение можно записать как
справа, это отношение можно записать как 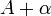 , где
, где 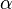 — O(1). Запишем это условие:
— O(1). Запишем это условие:
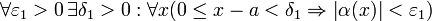 .
.
Зафиксируем 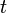 из отрезка
из отрезка 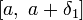 и применим теорему Коши ко всем
и применим теорему Коши ко всем 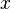 из отрезка
из отрезка  :
:
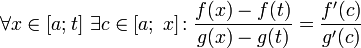 , что можно привести к следующему виду:
, что можно привести к следующему виду:
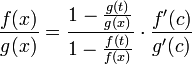 .
.
Для 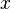 , достаточно близких к
, достаточно близких к 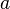 , выражение имеет смысл; предел первого множителя правой части равен единице (так как
, выражение имеет смысл; предел первого множителя правой части равен единице (так как 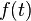 и
и 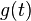 — константы, а
— константы, а 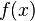 и
и 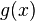 стремятся к бесконечности). Значит, этот множитель равен
стремятся к бесконечности). Значит, этот множитель равен 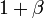 , где
, где  — бесконечно малая функция при стремлении
— бесконечно малая функция при стремлении 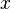 к
к 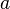 справа. Выпишем определение этого факта, используя то же значение
справа. Выпишем определение этого факта, используя то же значение  , что и в определении для
, что и в определении для 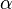 :
:
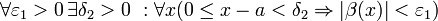 .
.
Получили, что отношение функций представимо в виде 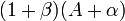 , и
, и 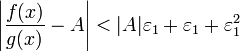 . По любому данному
. По любому данному  можно найти такое
можно найти такое 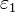 , чтобы модуль разности отношения функций и
, чтобы модуль разности отношения функций и 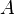 был меньше
был меньше  , значит, предел отношения функций действительно равен
, значит, предел отношения функций действительно равен 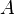 .
.
Если же предел 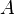 бесконечен (допустим, он равен плюс бесконечности), то
бесконечен (допустим, он равен плюс бесконечности), то
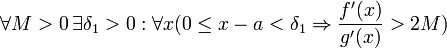 .
.
В определении  будем брать
будем брать 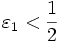 ; первый множитель правой части будет больше 1/2 при
; первый множитель правой части будет больше 1/2 при 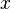 , достаточно близких к
, достаточно близких к 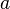 , а тогда
, а тогда 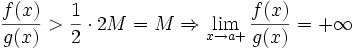 .
.
Для других баз доказательства аналогичны приведённым.
Примеры
· 
· 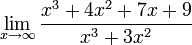
Здесь можно применить правило Лопиталя 3 раза, а можно поступить иначе. Нужно разделить и числитель, и знаменатель на x в наибольшей степени(в нашем случае 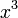 ). В этом примере получается:
). В этом примере получается:
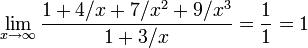
· 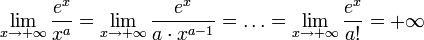 ;
;
· 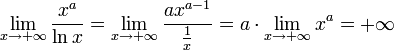 при
при 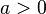 .
.
Исследование функции и построение ее графика
При построении графика функции необходимо провести ее предварительное исследование. Примерная схема исследования функции с целью построения ее графика имеет следующую структуру:
1. Область определения 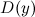 и область допустимых значений
и область допустимых значений 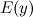 функции.
функции.
2. Четность, нечетность функции.
3. Точки пересечения с осями.
4. Асимптоты функции.
5. Экстремумы и интервалы монотонности.
6. Точки перегиба и промежутки выпуклости, вогнутости.
7. Сводная таблица.
Задание. Исследовать функцию 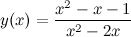 и построить ее график.
и построить ее график.
Решение. 1) Область определения функции.
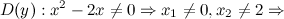
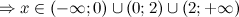
2) Четность, нечетность.
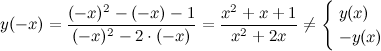
Функция общего вида.
3) Точки пересечения с осями.
а) с осью 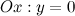 :
:
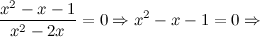
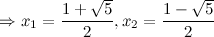
то есть точки 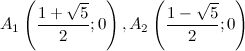
б) с осью 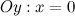 : в данной точке функция неопределенна.
: в данной точке функция неопределенна.
4) Асимптоты.
а) вертикальные: прямые 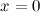 и
и 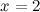 - вертикальные асимптоты.
- вертикальные асимптоты.
б) горизонтальные асимптоты:
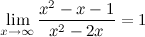
то есть прямая 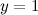 - горизонтальная асимптота.
- горизонтальная асимптота.
в) наклонные асимптоты 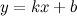 :
:
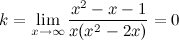
Таким образом, наклонных асимптот нет.
5) Критические точки функции, интервалы возрастания, убывания.
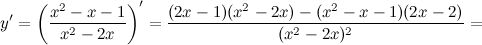
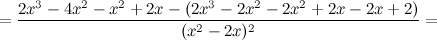
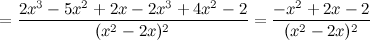
Найдем точки, в которых первая производная равна нулю или не существует: 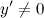 для любого
для любого  из области определения функции;
из области определения функции; 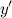 не существует при
не существует при 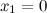 и
и 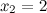 .
.

Таким образом, функция убывает на всей области существования. Точек экстремума нет.
6) Точки перегиба, интервалы выпуклости, вогнутости.
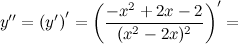
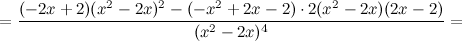
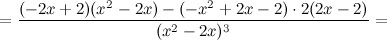
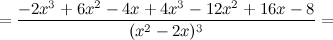
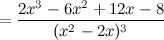
Найдем точки, в которых вторая производная равна нулю или не существует: 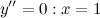 ; при
; при 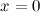 и
и 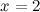 вторая производная не существует.
вторая производная не существует.
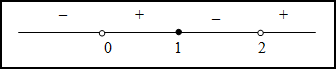
Таким образом, на промежутках 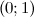 и
и 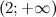 функция вогнута, а на промежутках
функция вогнута, а на промежутках 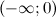 и
и 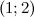 - выпукла. Так как при переходе через точку
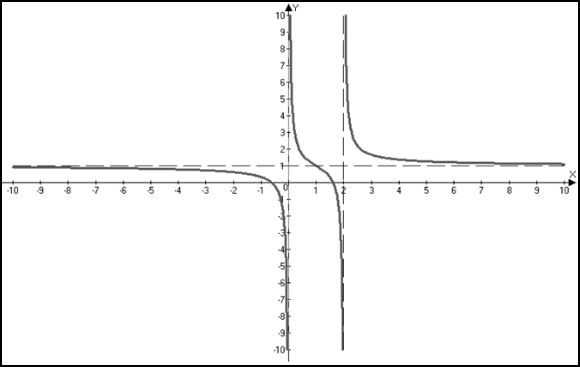
- выпукла. Так как при переходе через точку 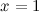 вторая производная поменяла знак, то эта точка является точкой перегиба.
вторая производная поменяла знак, то эта точка является точкой перегиба.
7) Эскиз графика.
17. Использование производной для исследования свойств функции и построения ее графика.
Связь между непрерывностью и дифференцируемостью функции. Если функция f ( x ) дифференцируема в некоторой точке, то она непрерывна в этой точке. Обратное неверно: непрерывная функция может не иметь производной.
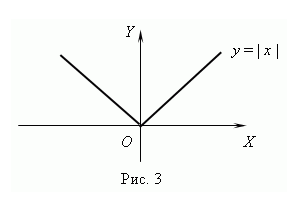
| П р и м е р . | Функция y = | x | ( рис.3 ) всюду непрерывна, но она не имеет производной при x = 0 , так как в этой точке не существует касательной к графику этой функции. ( Подумайте, почему ? ) |
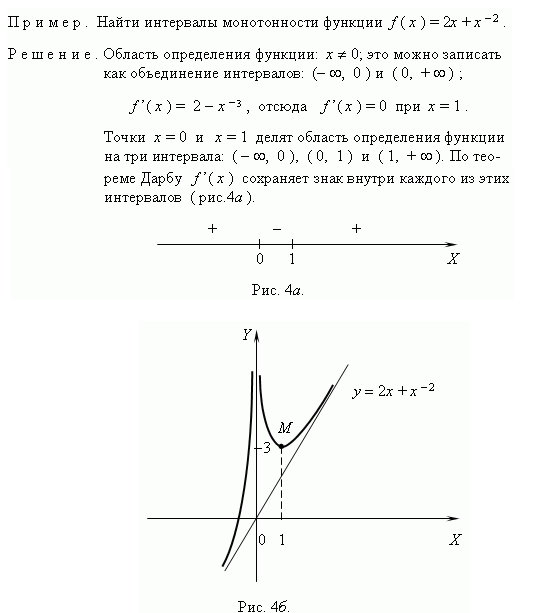
 План исследования функции. Для построения графика функции нужно:
План исследования функции. Для построения графика функции нужно:
1) найти область определения и область значений функции,
2) установить, является ли функция чётной или нечётной,
3) определить, является ли функция периодической или нет,
4) найти нули функции и её значения при x = 0,
5) найти интервалы знакопостоянства,
6) найти интервалы монотонности,
7) найти точки экстремума и значения функции в этих точках,
8) проанализировать поведение функции вблизи “особых” точек
и при больших значениях модуля x .
18. Определение и свойства неопределённого интеграла.
