Система линейных алгебраических выражений, равносильные СЛАУ

Система линейных алгебраических уравнений (СЛАУ), состоящая из m уравнений с n неизвестными x₁, …, x_n имеет следующий вид

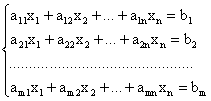
Числа a_11,12,…,n- называются коэффициентами при неизвестных, а числа b_1,2,…,n- свободными членами. Решением системы уравнений называется всякая упорядоченная совокупность чисел , которая будучи подставлена в систему на место неизвестных, обращает все уравнения системы в тождества. Система уравнений называется совместной, если имеет хотя бы одно решение, и несовместной, если не имеет решений. Совместная система уравнений называется определенной, если она имеет одно единственное решение, и неопределенной, если она имеет по крайне мере два различных решения.

Две системы уравнений называются равносильными или эквивалентными, если имеют одно и то же множество решений.

Свойства равносильности: 1) если к обеим частям неравенства прибавить одно и то же выражение, определенное на ОДЗ (область допустимых значений) исходного неравенства, то получиться неравенство, равносильное данному неравенству; 2)Если обе части неравенства умножить или разделить на одно и то же выражение, большее нуля, определенное на ОДЗ исходного неравенства, то получиться неравенство, равносильное данному неравенству; 3) Если обе части неравенства умножить или разделить на одно и то же выражение, меньшее нуля, определенное на ОДЗ исходного неравенства,а затем поменять знак неравенства на противоположный, то получиться неравенство, равносильное данному неравенству.

12. Решение СЛАУ методом Гаусса

В отличие от матричного метода и формул Крамера метод Гаусса является универсальным, так как применим для решения и исследования на совместность не только квадратных, но любых СЛАУ. Суть метода: СЛАУ кратко записывается в виде расширенной матрицы, которая с помощью элементарных преобразований над строками приводится к ступенчатому виду. Этот процесс называется прямым ходом метода Гаусса. Тогда каждой строке ступенчатой расширенной матрицы соответствует уравнение ступенчатой СЛАУ. Ступенчатая СЛАУ несовместна, если она содержит уравнение вида 0х₁ + 0х₂ +…+0х_n = С, (где С  0), соответствующее строке 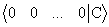расширенной матрицы, так как такому уравнению соответствует невыполнимое равенство 0 = С. Полностью нулевые строки 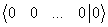расширенной матрицы вычеркиваются, так как они соответствуют тождеству 0х₁ + 0х₂ +…+0х_n  0, которое выполняется при любых значениях неизвестных х₁, х₂, …, х_n.

Решение совместной СЛАУ ступенчатого вида находят так: из последнего уравнения СЛАУ находят значение неизвестной x_n и подставляют в вышестоящее уравнение, чтобы найти значение неизвестной x_n1. Далее, используя значения этих двух неизвестных, поднимаются на ступеньку выше и находят значение неизвестной x_n2 и так далее. Последним находят значение неизвестной x₁ из 1-го уравнения ступенчатой СЛАУ. Описанный процесс называется обратным ходом метода Гаусса.