Решение уравнений и неравенств. В Maple 14 имеется встроенная функция solve(уравнение или неравенство, пе­ременная), предназначенная для решения уравнений и неравенств

В Maple 14 имеется встроенная функция solve(уравнение или неравенство, пе­ременная), предназначенная для решения уравнений и неравенств. Если уравне­ние или неравенство имеет одну переменную, то имя переменной в функции мож­но опустить.

Например, необходимо решить алгебраическое уравнение

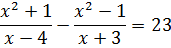
Для этого вводим уравнение:

> (x^2 + 1)/(x-4)-(х^2-1)/(х+3)=23

Уравнение набрано верно. С помощью функции solve() решаем уравнение:

> solve(%);

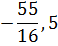
Решим следующее уравнение с параметрами

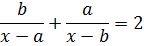
Вводим уравнение:

>b/(x-a) + a/(x+b)

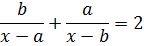
Поскольку переменных несколько, то необходимо указать переменную х, от­носительно которой решается уравнение:

> solve(%, x);

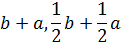
Получили два корня: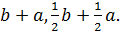

Проверку правильности решения можно осуществить встроенной функцией subs(), которая вычисляет значение выражения. Функция subs(x = a, f) имеет не­сколько аргументов, где х — переменная в выражении f; а — значение перемен­ной х.

Например, решаем уравнение

5х²+|х + 7|-13 = 0.

> solve(5*x^2 + abs(x+7) - 13 = 0);

Сделаем проверку:

> subs(x = 1, 5*х^2 + abs(x + 7) - 13 = 0);

-8 + |8| = 0

>subs(x = -6/5, 5*х^2 + abs(x + 7) - 13 = 0);

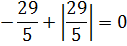
Решение верное.

Решим иррациональное уравнение

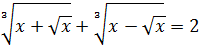
> (1 + sqrt(x))^(1/3) + (1 - sqrt(x))^(1/3) =2;

>solve(%);

С помощью функции solve() можно решать системы уравнений, при этом уравнения и неизвестные указываются в фигурных скобках {} через запятую [1]. Например, необходимо решить систему уравнений

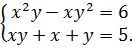
Решение будет следующим:

>solve({x^2*y-x*x^2 = 6,x*y+x+y=5},{x,y})

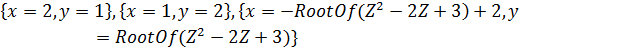
Действительных решений системы уравнений два: (2, 1) и (1, 2).

Для тригонометрического уравнения функция solve() по умолчанию возвраща­ет только один корень. Для возвращения множества корней необходимо исполь­зовать необязательный аргумент AUSolutions. Например,

> solve{sin{x) = 1/2, х, AllSolutions);

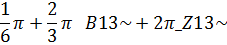
Форма ответа здесь необычная, однако корни уравнения найдены правильно. Переменная _В, независимо от индекса, принимает значения из множества {0, 1}, а значения Z принадлежат множеству целях чисел. Таким образом, полученное множество корней уравнения можно представить в виде

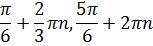
и записать в привычной форме

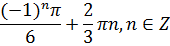
Решим тригонометрическое уравнение

3sin² 2х + 7cos2x - 3 = 0.

> solve{3*sin(2*x)^2 + 7*cos(2*x) - 3=0, х, AllSolutions);

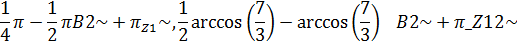
Решим систему тригонометрических уравнений

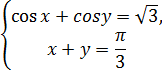
Решение следующие:

>solve({cos(x) + cos(y) = sqrt{3), х+у = Pi/3} ,{x, у});

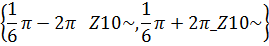
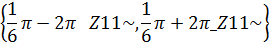
Ответ: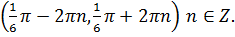

Теперь рассмотрим решение неравенств и систем неравенств. Например, решим иррациональное неравенство

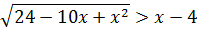
>solve(sqrt(24 - 10х + х*х) > х - 4);

RealRange(-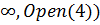

Решим неравенство

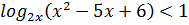
>solve( )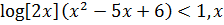

RealRange(Open(0),Open(1/2)),RealRange(Open(1),Open(2)), RealRange(Open(3),Open(6))

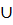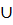Ответ: ( 0,1/2) (l,2) (3,6).

Контрольные вопросы

1. В каком порядке выполняются арифметические операции?

2. Каково назначение скобок при записи выражений?

3. Как записать степень числа в программе Maple?

4. Какое назначение имеет ! (восклицательный знак) на панели инструментов?

5. Как преобразовать градусы в радианы?

6. Как получить числовое значение функции?

7. Как вычислить натуральный логарифм числа?

8. Как получить приближенное значение действительного числа в Maple (c заданным числом значащих цифр)?

9. Какой командой осуществляется вызов библиотеки подпрограмм?

10. Какие функции преобразования математических выражений вы знаете?

11. Как упростить иррациональное число?

12. Как осуществить подстановку в выражении?

13. Как при преобразовании выражения указать диапазон изменения переменной?

14. Как с помощью функции solve()получить множество решений для тригонометрических уравнений?

Контрольные задания

1. Оформите титульный лист к лабораторной работе, согласно требованиям СФМЭИ (ТУ). Укажите название лабораторной работы. Фамилию, Имя, группу, номер студента в журнале (см. Приложение 1).

2. Создайте документ Maple. Напишите заголовок 14 кеглем, полужирно, с выравниванием по центру: «Лабораторная работа №1». Далее с выравниванием по правому краю, курсивом, 14 кеглем укажите полностью Фамилию, Имя, номер в журнале.

3. Выполните задания из своего варианта, определяемого номером в журнале. Каждое задание должно быть оформлено в отдельной секции (пиктограммы ) с заголовком «Задание №_». Завершать секцию должен развернутый ответ.

4. Распечатайте лабораторную работу из под программы Maple на листах формата А4 (односторонняя печать).

При выполнении контрольных заданий студенту необходимо подставить вместо буквенных параметров индивидуальные анкетные характеристики:

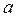- число букв в фамилии студента,

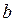- число букв в полном имени студента,

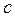- номер студента по списку в журнале.

В отчете на титульном листе необходимо обязательно указать, какие анкетные данные использовались при выполнении контрольных заданий (имя, фамилия, номер варианта).