Центр параллельных сил и центр тяжести твердого тела.

Условия равновесия произвольной пространственной системы сил

Из основной теоремы статики вытекает условие равновесия произвольной системы сил.

Векторная форма

Для равновесия произвольной системы сил, приложенных к твердому телу, необходимо и достаточно, чтобы главный вектор системы сил был равен нулю и главный момент системы сил относительно любого центра приведения также был равен нулю.

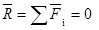
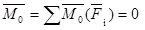
Алгебраическая форма.

Для равновесия произвольной системы сил, приложенных к твердому телу, необходимо и достаточно, чтобы три суммы проекций всех сил на оси декартовых координат были равны нулю и три суммы моментов всех сил относительно трех осей координат также были равны нулю.

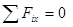
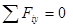
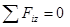
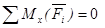
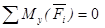
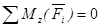
Условия равновесия пространственной системы параллельных сил.

Пусть на тело действует система параллельных сил. Расположим ось Oz параллельно силам.

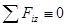
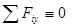
Уравнения 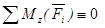выполняются тождественно. Условия определяются оставшимися уравнениями.

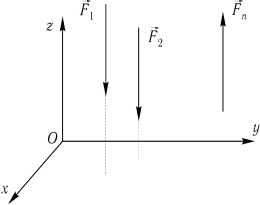
Для равновесия пространственной системы параллельных сил, действующих на твердое тело, необходимо и достаточно, чтобы алгебраическая сумма этих сил была равна нулю и суммы моментов этих сил относительно двух координатных осей, перпендикулярным силам, также были равны нулю.

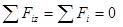
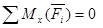
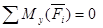
Здесь 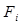-алгебраическая величина силы .

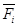Условия равновесия плоской системы сил.

Расположим оси Ох и Оу в плоскости действия сил. Так как ось Oz перпендикулярна силам, то

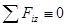выполняется для всех плоских систем сил, т. е. является тождеством. Каждая из сил расположена в одной плоскости с осями координат Ох и Оу, и поэтому ее моменты

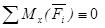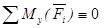относительно этих осей равны нулю. Таким образом, условия равновесия итоже становятся тождествами. Моменты сил относительно оси Oz, перпендикулярной силам, равны алгебраическим моментам этих сил относительно точки О. То есть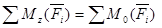

В результате из шести условий для произвольной системы сил после отбрасывания тождеств имеем следующие первая (основная) форма условий равновесия плоской системы сил:

(*)

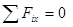
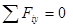
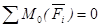т. е. для равновесия плоской системы сил, действующих на твердое тело, необходимо и достаточно, чтобы суммы проекций этих сил на каждую из двух прямоугольных осей координат,расположенных в плоскости действия сил, были равны нулю и сумма алгебраических моментов сил относительно любой точки, находящейся в плоскости действия сил, также была равна нулю.

Вторая форма

Для равновесия плоской системы сил, необходимо и достаточно чтобы алгебраические суммы величин моментов этих сил относительно трех точек, лежащих в плоскости действия сил и не расположенных на одной прямой, равнялись нулю:

(**)

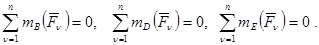Эта форма равновесия плоской системы сил также называется теоремой о трех моментах.

Доказательство необходимости: Пусть плоская система сил, находится в равновесии: 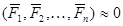. Из необходимости третьего уравнения (*) следует необходимость условий (*).

Доказательство достаточности: Пусть выполняются условия (**). Предположим (метод от противного), что плоская система сил ( 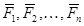), не находится в равновесии. Приведем эту систему сил к центру В, тогда 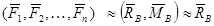,т.к.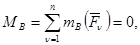

Если 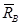= 0, то система сил находится в равновесии. Предположим, что 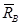¹0, т. е. что система сил не находится в равновесии. Применив дважды теорему Вариньона для точек D и E, получим: 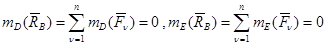. Из этих соотношений следует, что линия действия равнодействующей 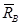, приложенной в точке B, проходит также через точки D и E, чего быть не может, так как точки B, D и E не расположены на одной прямой. Следовательно, наше предположение неверно и плоская система сил ( 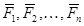) находится в равновесии. ■

Третья форма

Для равновесия плоской системы сил необходимо и достаточно, чтобы алгебраические суммы величин моментов этих сил относительно двух произвольно расположенных точек на плоскости действия сил равнялись нулю и сумма проекций всех сил на прямую, лежащую в этой плоскости и не перпендикулярную прямой, проходящую через эти две точки, также равнялась нулю:

(***)

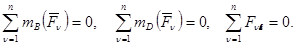Доказательство необходимости: Пусть плоская система сил находится в равновесии: 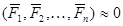. Из необходимости условий (*) следует необходимость условий (***).

Доказательство достаточности: Пусть выполняются условия (***). Предположим (метод от противного), что плоская система сил 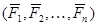не находится в равновесии. Приведем эту систему сил к центру В, тогда 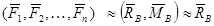,т.к.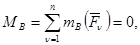

Если 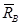= 0, то система сил находится в равновесии. Предположим, что 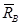¹ 0, т. е. что система сил не находится в равновесии. Применив теорему Вариньона для точки D, получим:

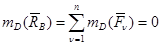.Из этого соотношения следует, что линия действия равнодействующей 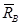, приложенной в точке B, проходит также через точку D. Из третьего уравнения соотношений (***) следует, что 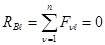. Таким образом, мы получили, что проекция равнодействующей 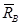, линия действия которой проходит через точку D, на прямую, не перпендикулярную прямой, проходящей через точки B и D, равняется нулю, чего быть не может. Следовательно, наше предположение неверно и плоская система сил 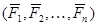, находится в равновесии. ■

Центр параллельных сил и центр тяжести твердого тела.

Центром системы параллельных сил называется точка пересечения линий действия равнодействующих систем параллельных сил, при любых поворотах этих сил около их точек приложения в одну и ту же сторону и на один и тот же угол.

Для нахождения положения центра системы параллельных сил определим его радиус-вектор при условии, что известны параллельные силы и радиус-векторы точек их приложения

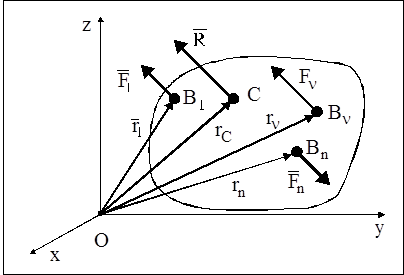
Пусть имеется система параллельных сил 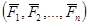, направление которых характеризуется единичным вектором 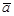. Каждую из параллельных сил можно представить в ви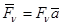де: , где 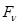– проекция силы на направление .

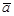Равнодействующая системы параллельных сил равна:

(*)

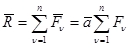Моменты относительно точки О находятся в виде:

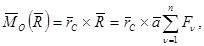
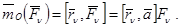
запишем теорему Вариньона относительно точки О: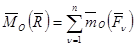

С учетом ранее найденных выражений: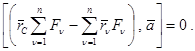

Так как центр параллельных сил, а, следовательно, и его радиус-вектор не зависят от направления параллельных сил, характеризуемого единичным вектором 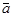, то полученное условие должно выполняться при любом направлении этого вектора. Это возможно только при обращении в нуль векторной величины, стоящей в скобках, откуда:

. (**)

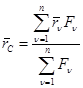Координаты центра системы параллельных сил определяются после проектирования выражения на оси декартовой системы координат:

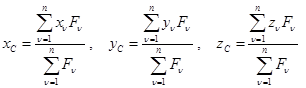
Центром тяжести тела называется центр С системы параллельных сил тяжести 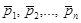материальных частиц этого тела, определяемый на основании (**) формулой:

,

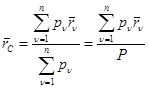где 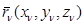- радиус – вектор n –й частицы, 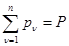- вес тела .

Спроектировав найденное выражение на оси декартовой системы координат, получим координаты центра тяжести в виде:

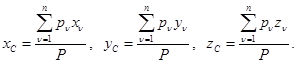
Для однородного материального объема v с учетом, что 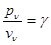(g - вес единицы объема, v_n – объем n-й части НМС) они примут вид:

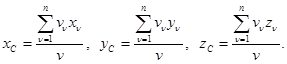
а если в них перейти к пределу при n®¥:

;

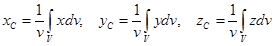Трение скольжения

Опыт показывает, что при стремлении двигать одно тело по поверхности другого в плоскости соприкосновения тел возникает сила сопротивления их относительному скольжению. Эту силу, называют силой трения скольжения.

Если твёрдое тело находится на абсолютно гладкой поверхности другого тела в равновесии, то реакция связи направлена по нормали к поверхности.

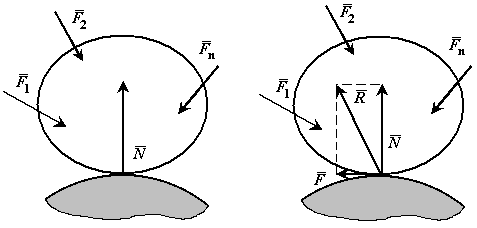В действительности абсолютно гладких поверхностей не бывает. Все поверхности тел в той или иной степени шероховаты. Поэтому сила реакции 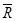шероховатой поверхности при равновесии тела зависит от активных сил не только по числовой величине, но и по направлению.

Разложим силу реакции 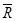шероховатой поверхности на составляющие: одну из которых 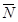направим по общей нормали к поверхности соприкосновения, а другую 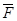направим в касательной плоскости к этим поверхностям.

Силой трения скольжения (или просто силой трения) называется составляющая силы реакции связи, которая лежит в касательной плоскости к поверхностям соприкасающихся тел.

Силой нормальной реакцией связи называется составляющая силы реакции связи, которая направлена по общей нормали к поверхностям соприкасающихся тел.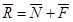

Сухим трением называется трение, когда между поверхностями соприкасающихся тел нет смазывающего вещества.

Будем рассматривать два случая: трения при покое или равновесии тела и трение скольжения при движении одного тела по поверхности другого с некоторой относительной скоростью.

При покое сила трения зависит только от активных сил. При выбранном направлении касательной в точке соприкосновения поверхностей тел сила трения вычисляется по формуле: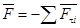

Аналогично при выбранном направлении нормали нормальная реакция выражается через заданные силы: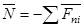

При движении одного тела по поверхности другого сила трения является постоянной величиной.

В инженерных расчетах обычно исходят из ряда установленных опытным путем закономерностей, которые с достаточной для практики точностью отражают основные особенности явления сухого трения. Эти закономерности называются законами трения скольжения или законами Кулона.

Законы Кулона

1. Сила трения скольжения находится в общей касательной плоскости соприкасающихся поверхностей тел и направлена в сторону, противоположную направлению возможного скольжения тела под действием активных сил. Сила трения зависит от активных сил, и её модуль заключён между нулём и максимальным значением, которое достигается в момент выхода тела из положения равновесия, то есть:

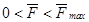
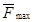- называется предельной силой трения.

2. Предельная сила трения скольжения при прочих равных условиях не зависит от площади соприкосновения трущихся поверхностей. Из этого закона следует, что для того чтобы сдвинуть, например кирпич, надо приложить одну и туже, силу, независимо, от того, какой гранью он положен на поверхность, широкой или узкой.

3. Предельная сила трения скольжения пропорциональна нормальной реакции (нормальному давлению), то есть

,

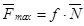где безразмерный коэффициент 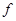называют коэффициентом трения скольжения; он не зависит от нормальной реакции.

4. Коэффициент трения скольжения зависит от материала и физического состояния трущихся поверхностей, то есть от величины и характера шероховатости, влажности, температуры и других условий. Коэффициент трения устанавливается экспериментально.

Считается, что коэффициент трения не зависит от скорости движения.

Угол трения

Многие задачи на равновесие тела на шероховатой поверхности, т.е. при наличии трения, удобно решать геометрически. Для этого введем понятие угла и конуса трения.

Реакция реальной (шероховатой) связи 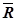слагается из двух составляющих: нормальной реакции 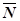и перпендикулярной ей силы трения 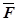. Следовательно, реакция связи 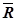отклоняется от нормали к поверхности на некоторый угол. При изменении силы трения от нуля до максимальной, сила реакции 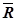меняется от нуля до 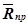, а ее угол с нормалью растет от нуля до некоторого предельного значения .

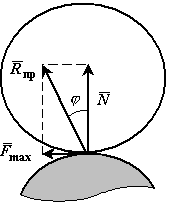Углом трения называется наибольший угол 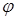между предельной силой реакции шероховатой связи 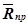и нормальной реакцией .

; ;.

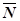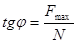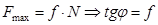Угол трения зависит от коэффициента трения.

Конусом трения называют конус, описанный предельной силой реакции шероховатой связи 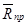вокруг направления нормальной реакции.

Для равновесия твёрдого тела на шероховатой поверхности необходимо и достаточно, чтобы линия действия равнодействующей активных сил, действующих на твёрдое тело, проходила внутри конуса трения или по его образующей через его вершину.

Тело нельзя вывести из равновесия любой по модулю активной силой, если её линия действия проходит внутри конуса трения.

Трение качения

Трением качения называется сопротивление, возникающее при качении одного тела по поверхности другого.

Рассмотрим цилиндрический каток радиуса r на горизонтальной плоскости. Под действием активных сил каток может катиться по плоскости. Однако в месте соприкосновения катка и плоскости из-за деформации поверхностей могут возникнуть реакции, препятствующие не только скольжению, но и качению.

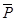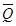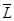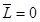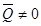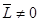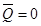Активные силы, действующие на катки в виде колес, обычно состоят из силы тяжести , горизонтальной силы , приложенной к центру катка, и пары сил с моментом , стремящейся катить колесо. Колесо в этом случае называется ведомо-ведущим. Если , а , то колесо называется ведомым.Если , а , то колесо называется ведущим.

Соприкосновение катка с неподвижной плоскостью из-за деформации катка и плоскости происходит не в точке, а по некоторой линии BD. По этой линии на каток действуют распределенные силы реакции. Если привести силы реакции к точке А, то в этой точке получим главный вектор 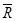этих распределенных сил с составляющими 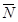(нормальная реакция) и 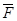(сила трения скольжения), а также пару сил с моментом .

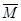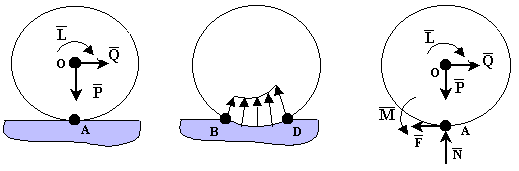Рассмотрим равновесие катка. Система сил – плоская. Запишем уравнения равновесия системы сил.

(x)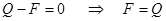

(y)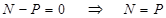

(M_A)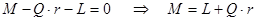

Момент 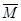называется моментом трения качения. Наибольшее значение М достигается в момент начала качения катка по плоскости.

Установлены следующие приближенные законы для наибольшего момента пары сил, препятствующих качению.

1. Наибольший момент пары сил, препятствующих качению, в довольно широких пределах не зависит от радиуса катка.

2. Предельное значение момента 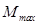пропорционально нормальной реакции .

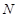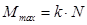. ( k имеет это размерность длины)

Коэффициент пропорциональности k называют коэффициентом трения качения при покое.

3. Коэффициент трения качения k зависит от материала катка, плоскости и физического состояния их поверхностей. Коэффициент трения качения при качении в первом приближении можно считать не зависящим от угловой скорости качения катка и его скорости скольжения по плоскости.

Для вагонного колеса по рельсу 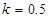мм.

Рассмотрим движение ведомого колес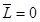а. , а .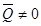

Качение колеса начнется, когда выполнится условие 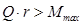или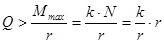

Скольжение колеса начнется, когда выполнится условие .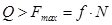

Обычно отношение 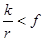и качение начинается раньше скольжения.

Если 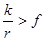, то колесо будет скользить по поверхности, без качения.