С помощью маятника Обербека
ЦЕЛЬ: получить экспериментальную зависимость углового ускорения от момента силы и определить момент инерции маятника динамическим методом.
ОБОРУДОВАНИЕ: маятник Обербека, секундомер, штангенциркуль, линейка, набор грузов.
 |
ОПИСАНИЕ УСТАНОВКИ
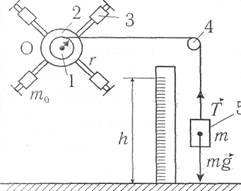
Основной частью установки является крестообразный маятник, который может вращаться с малым трением вокруг оси О (см. рисунок).
| Рис. 1 |
По стержням крестовины могут перемещаться подвижные цилиндры 3 массой т0 .На одной оси с крестовиной насажены шкивы 1 и 2 разного радиуса r. К концу нити, намотанной на один из шкивов и перекинутой через невесомый блок 4, прикрепляется груз 5 массой m, приводящий маятник во вращательное движение. Время прохождения грузом расстояния h измеряют секундомером. Маятник в исходном положении удерживается электромагнитом, при нажатии клавиши "Пуск" секундомера электромагнит отключается, груз начинает двигаться и одновременно включается секундомер. Счёт времени заканчивается при достижении грузом нижнего положения. Для того, чтобы секундомер сработал, необходимо установке с помощью винтов в основании платформы придать такое положение, при котором груз опускался бы точно в отмеченный круг. В этот круг вмонтирован датчик, выключающий секундомер.
Расстояние h, отмечается по линейке, установленной в верхней части установки, на которой указывается расстояние груза в начальном положении от основания установки.
ОПИСАНИЕ МЕТОДА ИЗМЕРЕНИЙ
Приняв, что нить невесома, нерастяжима, считаем движение грузов равноускоренным. Ускорение груза а определяют, измерив время его движения и пройденный путь h.
а=2h/t2. (9)
Угловое ускорение маятника α выразим через линейное ускорение и радиус шкива r:
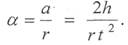 (10)
(10)
Силу натяжения нити Т можно определить, применив к движению груза массой т закон Ньютона (пренебрегая при этом сопротивлением воздуха):
Т=т(g-а)≈тg,
так как обычно а«g.
Таким образом, измерив для груза массой т время t прохождения им расстояния h, можно рассчитать угловое ускорение α (формула 10) маятника и определить момент силы, действующий на маятник:
М=Тr=тgr. (11)
При вращении маятника на него действует также тормозящий момент сил трения МТР, и поэтому закон динамики (2.8) принимает вид
Iα=М-МТР. (12)
Это уравнение позволяет найти момент инерции блока I динамическим методом, измерив ряд величин α и М. Для более точного определения величины I в опыте получают зависимость α=f(М), линейный характер которой (при
МТР =const) позволяет рассчитать среднее значение I по угловому коэффициенту опытной прямой.
Задание 1.Изучение закона вращения маятника
1. Определите массу грузов т, установите центры подвижных цилиндров m0 на одинаковом расстоянии l от оси вращения и измерьте радиусы шкивов r1 и r2. Результаты запишите в табл. 1.
Таблица 1
| h= м, | |||||
| r, мм | № | т, г | t, с | М, Н∙м | α, с-2 |
| r1= | |||||
| r2= | |||||
| Координаты средней точки |
3. Прикрепите к нити один из грузов т. Вращая маятник, намотайте нить на малый шкив r1 в один слой и включите электромагнит красной кнопкой, расположенной в верхней части установки. Запишите расстояние h, проходимое грузом при падении. Убедитесь, что нить и груз во время движения не задевают неподвижные части установки или другие предметы. Устраните качание груза и нажмите кнопку «Пуск» секундомера. Запишите время t движения груза до нижней точки.
4. С тем же шкивом, увеличивая массу груза т (не менее 4-х раз), запишите
время t движения груза на пути h. Все результаты по мере их получения записывайте в табл. 1.
5. Аналогичные измерения проведите, используя шкив радиусом rг.
6. Вычислите значения α и М вкаждом опыте по формулам (10, 11).
7. Используйте рекомендации из п.3.1, изобразите графически зависимость
углового ускоренна α от момента силы М, нанеся точки для обоих шкивов на
один график.
8. По графику определите среднее значение момента инерции маятника
I=ΔМ/Δα, рассчитав угловой коэффициент прямой.
9. По графику определите момент сил трения, сравните его с моментами,
создаваемыми грузами, и сделайте вывод.
10. Рассчитайте относительную δΙ и абсолютную ΔΙ погрешности момента
инерции (см. указания из п. 3.3),
11. Запишите результат в виде доверительного интервала
I=I±ΔΙ; Р=1-(1/2)N-1
с доверительной вероятностью Р, оценённой по формуле (4).
Задание 2.Измерение динамическим методом момента инерции крестовины маятника
1. Закрепите подвижные цилиндры на максимальном и одинаковом расстоянии l от оси вращения. Прикрепите к нити груз массой m. Выберите для эксперимента один шкив, измерьте его радиус r и запишите в табл. 2 значения m, r и h.
Таблица 2
| h= м , т= кг, r = мм | ||||
| № | l, см | t, с | l2, см2 | I, кг∙м2 |
| … | ||||
| - | ||||
 |  | 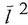 | 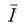 |
2. Вращая маятник, намотайте нить на шкив в один слой и измерьте время движения t (см. п. 3 задания 1).
5. Проведите ещё 6 опытов с тем же грузом т, уменьшая всякий раз на 1,5–2 см расстояние цилиндров l от оси вращения. Результаты измерений l и t вносите в табл. 2.
4. Вычислите для каждого опыта величины l2 и момент инерции маятника по формуле, полученной сучётом выражений (10), (11):
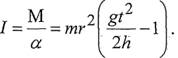 (13)
(13)
5. Постройте график зависимости момента инерции маятника I от l2 (см. рекомендации п. 3.1). Сделайте вывод о характере полученной зависимости I=f(l2) с учётом того, что момент инерции маятника, у которого цилиндры приняты за материальные точки,
I=Iкр+4m0l2. (14)
6. Определите с помощью графика (динамическим методом) момент инерции крестовины Iкр, которой согласно (14) равен параметру b линейной зависимости I=f(l2).
7. Рассчитайте массу подвешенных грузов т0. 8. Сделайте выводы.
Контрольные вопросы
1. Запишите закон динамики вращательного движения.
2. Какое вращение тела называют равноускоренным, каковы его условия?
3. Как направлены векторы 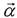 ,
, 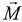 момент импульса тела
момент импульса тела 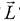 ?
?
4. От чего зависят: а) угловое ускорение маятника, б) момент инерции маятника, в) момент силы, действующий на маятник?
5. Какая зависимость лежит в основе динамического метода измерения момента инерции I?
6. Какие величины определяют наклон прямой на графике α=f(М)?
7. Как в работе изменяют момент силы?
8. Какие величины в работе измеряют для определения величин α и М?
9. Как можно изменять момент инерции маятника в данной работе?
