Тестовые задания для самостоятельной работы. 2.Рассчитать линейный коэффициент парной корреляции, тем самым, оценив тесноту связи изучаемых явлений.
(ОК-1; ПК-9.)
Раздел 1:
1.
2.Рассчитать линейный коэффициент парной корреляции, тем самым, оценив тесноту связи изучаемых явлений.
1) 0,2;
2) 0,89;
3) -0,8.
3.На сколько в среднем расчетные значения отклоняются от фактических? Вычислить среднюю ошибку аппроксимации.
1) 0,2;
2) 6,22;
3) 8,22.
4 .Найти долю дисперсии, объясняемую регрессией в общей дисперсии результативного признака, то есть рассчитайте коэффициент детерминации в %.
1) 79,3;
2) 80;
3) 93.
5 . Выполнить сравнение фактического и критического (табличного) F значений F-критерия Фишера и выполнить проверку гипотезы Ho о статистической незначимости уравнения регрессии и показателя тесноты связи. Обоснуйте ответ.
1) Fфакт > Fтабл;
2) Fфакт < Fтабл.
6 . Рассчитать прогнозное значение результативного признака на 110%
1) 68,514;
2) 62,29;
3) 19,13.
7. Представить данный пример в виде степенной (нелинейной) модели и путем линеаризации переменных составить уравнение степенной регрессии.
1) Yx = -0,77+1,29x;
2) Yx = 0,77+1,29x;
3) Yx = 0,77-1,29x.
8.Выполнить потенцирование уравнения.
1) 0,169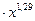 
;
2) 1,29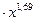 
.
9.Рассчитайте индекс корреляции степенной модели для нелинейной регрессии.
1) 0,2;
2) 0,886;
3) -0,1.
10.Рассчитайте индекс детерминации в данном примере.
1) 0,77;
2) 0,886;
3) 0,784.
11. Статистическая надежность оценки коэффициентов регрессии увеличивается:
1) - с увеличением числа степеней свободы;
2) - с уменьшением числа степеней свободы;
3) - с не зависит от числа степеней свободы.
12. Добавление новой объясняющей переменной:
1) – никогда не уменьшает значение коэффициента детерминации;
2) – иногда уменьшает значение коэффициента детерминации;
3) – не оказывает влияния на значение коэффициента детерминации.
13. Проверка статистического качества уравнения регрессии включает:
1) – поверка статистической значимости коэффициентов уравнения, общего качества уравнения, выполнимости предпосылок МНК;
2) – проверку статистической значимости коэффициентов уравнения и выполнимости предпосылок МНК;
3) – вычисление доверительных интервалов зависимой переменной и проверку общего качества уравнения.
Раздел 2:
(ОК-1; ПК-10.)
1. Укажите истинное утверждение:
1) – скорректированный и обычный коэффициент детерминации совпадают только в тех случаях, когда обычный коэффициент детерминации равен единице или нулю;
2) – стандартные ошибки коэффициентов регрессии определяются значениями всех коэффициентов регрессии;
3) – при наличии гетероскедастичности оценки коэффициентов регрессии становятся смещенными.
2. Если коэффициент детерминации равен нулю, то критерий Фишера равен:
1) – нулю;
2) – единице;
3) – больше или равен единице.
3. Для чего может быть использована модель, построенная и верифицированная на основе (уже имеющихся) наблюденных значений объясняющих переменные?
1) Для прогноза значений зависимой переменной в будущем или для других наборов значений объясняющих переменных.
2) Для прогноза значений зависимой переменной в будущем.
3) Для анализа значений зависимой переменной в прошлом или для других наборов значений объясняющих переменных.
4) Для анализа значений зависимой переменной в настоящем или для других наборов значений объясняющих переменных.
4. Какие основные классы модели, которые применяют для анализа и/или прогноза, можно выделить?
1) модели временных рядов, модели постоянных рядов;
2) модели временных рядов, регрессионные модели с одним уравнением, система одновременных уравнений;
3) регрессионные модели с одним уравнением, система одновременных уравнений;
4) модели постоянных рядов, регрессионные модели с одним уравнением, система одновременных уравнений.
5. К моделям временных рядов относятся:
1) Модели тренда, модель сезонности;
2) Модели сезонности, модель спроса и предложения, модель тренда;
3) Модель тренда, модель сезонности, модель тренда и сезонности;
4) Модели сезонности, модель спроса и предложения; модель тренда и сезонности.
6. К какому классу моделей относится модель спроса и предложения?
1) К модели временных рядов;
2) К модели постоянных рядов;
3) К регрессионной модели с одним уравнением;
4) К системе одновременных уравнений.
7. Какие типы данных встречаются при моделировании экономических процессов?
1) Пространственные данные и временные ряды.
2) Пространственные данные и постоянные ряды.
3) Временные и постоянные ряды.
4) Пространственные данные, временные и постоянные ряды.
8. К какому типу данных относится набор сведений:
1) Пространственные данные.
2) Временные ряды.
3) Постоянные ряды.
4) Временные и постоянные ряды.
9. К какому виду данных относятся ежеквартальные данные по инфляции, средней заработной плате, национальному доходу, денежной эмиссии за последние годы?
1) К пространственным данным.
2) К постоянным рядам.
3) К временным рядам.
4) К пространственно-временным данным.
10. Укажите верное утверждение о скорректированном коэффициенте детерминации:
1) – скорректированный коэффициент детерминации меньше обычного коэффициента детерминации для m> 1;
2) – скорректированный коэффициент детерминации больше обычного коэффициента детерминации для m> 1;
3) – скорректированный коэффициент детерминации меньше или равен обычному коэффициенту детерминации для m> 1.
11. С увеличением числа объясняющих переменных скорректированный коэффициент детерминации:
1) – растет медленнее, чем обычный коэффициент детерминации;
2) – не изменяется;
3) – превышает значение обычного коэффициента детерминации.
12. Скорректированный коэффициент детерминации увеличивается при добавлении новой объясняющей переменной тогда и только тогда:
1) – когда t- статистика для этой переменной по модулю больше единицы;
2) - когда t- статистика для этой переменной по модулю больше своего критического значения;
3) – когда t- статистика для этой переменной по модулю больше трех.
13. Если коэффициент детерминации равен нулю, то:
1) – величина зависимой переменной Y линейно не зависит от независимых переменных Xi;
2) – величина зависимой переменной Y линейно зависит от независимых переменных Xi;
3) – нельзя сделать вывод о линейной зависимости Y от независимых переменных Xi.
14. При добавлении существенной объясняющей переменной X в линейную модель множественной регрессии скорректированный коэффициент детерминации:
1) – увеличивается;
2) – уменьшается;
3) – не изменяется.
Типовой вариант контрольной работы(ОК-1; ПК-9.)
1. Недельные изменения курса акций (ден. ед.) акционерного общества представлены в табл. 1. помощью критерия «восходящих» и «нисходящих» серий с вероятностью 0,95 сделать вывод о присутствии или отсутствии тенденции во временном ряду.
Таблица 1
| t | ||||||||||||||||||||
| yt | ||||||||||||||||||||
| t | ||||||||||||||||||||
| yt | ||||||||||||||||||||
2. В табл. 23 представлены квартальные данные об объеме производства продукции (ден. ед.). Определить прогноз производства в третьем квартале 2012 г. с помощью среднего прироста.
Таблица 2
| квартал | 1-й 2011г. | 2-й 2011г | 3-й 2011г | 4-й 2011г | 1-й 2012г | 2-й 2012г |
| yt | 21,19 | 22,24 | 23,27 | 24,32 | 25,35 | 26,38 |
3. Ежеквартальная динамика процентной ставки банка дана в табл. 3. С помощью среднего темпа роста определить прогноз процентной ставки банка в четвертом квартале 2012 г.
Таблица 3
| квартал | 1-й 2011г. | 2-й 2011г | 3-й 2011г | 4-й 2011г | 1-й 2012г | 2-й 2012г | 3-й 2012г |
| yt | 7,3 | 7,9 | 8,9 | 9,6 | 10,8 | 11,6 | 13,0 |
4. Временной ряд, характеризующий изменение выпуска продукции, представлен в табл. 4. Используя метод «восходящих» и «нисходящих» серий с вероятностью 0,95, сделать один из следующих выводов:
• в тенденция во временном ряду присутствует;
• тенденция во временном ряду отсутствует.
Таблица 4
| t | ||||||||||
| yt | ||||||||||
| t | ||||||||||
| yt |
5. По критерию «восходящих» и «нисходящих» проверить наличие тенденции в изменении курса валюты (табл. 5). Вывод сделать с доверительной вероятностью 0,95.
Таблица 5
| t | |||||||||||||||||
| yt | 28,54 | 28,58 | 28,52 | 28,57 | 28,62 | 28,61 | 28,65 | 28,63 | 28,68 | 28,66 | |||||||
| t | |||||||||||||||||
| yt | 28,71 | 28,72 | 28,70 | 28,74 | 28,76 | 29,0 | 28,95 | 28,97 | 29,04 | 29,05 | |||||||
6. Данные об изменении урожайности пшеницы (ц/га) за 10 лет представлены в табл. 6. Произвести сглаживание по трех- и пятилетней скользящей средней и по пятилетней взвешенной скользящей средней.
Таблица 6
| t | ||||||||||
| yt | 16,3 | 21,2 | 18,1 | 8,7 | 16,3 | 17,3 | 20,9 | 15,4 | 19,7 | 21,7 |
7. В табл. 7 приведена доля докторов наук в высших учебных заведениях РФ (%) по годам. Произвести сглаживание временного ряда с использованием экспоненциальной средней, приняв параметры сглаживания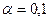 
и 
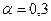. По результатам расчетов определить, какой из сглаженных временных рядов носит более гладкий характер.
Таблица 7
| годы | |||||
| yt | 8,95 | 9,5 | 10,01 | 10,93 | 10,08 |
8. Дан временной ряд (табл. 8), характеризующий месячную динамику численности (чел.), занятых в сфере услуг фирмы.
| Таблица 8 | |||||||||||||||
| t | |||||||||||||||
| yt |
В предположении об изменении тенденции ряда по линейной модели найти коэффициенты тренда
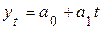
и рассчитать точечный прогноз на 16-й месяц.
В предположении об изменении тенденции ряда по параболической модели найти коэффициенты тренда
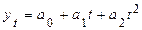
и точечный прогноз на 16-й месяц.
В предположении об изменении тенденции ряда по показательной модели найти коэффициенты тренда yt = abt и определить точечный прогноз на 16-й месяц.
9. Для прогнозирования временного ряда объема реализованной продукции выбрана линейная модель
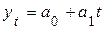
Длина временного ряда n = 24, значение критерия Дарбина - Уотсона d = 1,4. Определить справедливость одного из следующих вариантов адекватности модели:
• модель неадекватна реальному процессу по данному критерию;
• модель адекватна реальному процессу по данному критерию;
• нет достаточных оснований для принятия решения об адекватности модели.
10. В табл. 9 приведены данные об объеме автомобильных перевозок фирмы (тыс. т). В табл. 10 приведены прогнозные значения этого показателя, полученные по 1-й и 2-й моделям. Сравнить точность 1-й и 2-й моделей на основе средней относительной ошибки по модулю и определить, какая модель является более точной.
Таблица 9
| Месяц | 01.13 | 02.13 | 03. 13 | 04. 13 | 05. 13 | 06.013 | 07. 13 |
| t | |||||||
 |
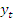Таблица 10
| t | |||||||
| 1-я модель, уt | |||||||
| 2-я модель, yt |
Типовой вариант контрольной работы(ОК-1; ПК-10.)
Задача : Даны системы эконометрических уравнений:
Модель протекционизма Сальватора (упрощенная версия):
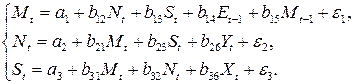
Требуется:
1.Применив необходимое и достаточное условие идентификации, определите, идентифицируемо ли каждое из уравнений модели.
2.Определите метод оценки параметров модели.
3.Запишите в общем виде приведенную форму модели.
где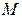 
– доля импорта в ВВП; 
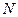– общее число прошений об освобождении от таможенных пошлин; 
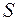– число удовлетворенных прошений об освобождении от таможенных пошлин; 
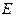– фиктивная переменная, равная 1 для тех лет, в которые курс доллара на международных валютных рынках был искусственно завышен, и 0 – для всех остальных лет; 
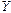– реальный ВВП; 
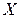– реальный объем чистого экспорта; 
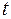– текущий период; 
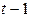– предыдущий период.
Задача. По 20 предприятиям региона изучается зависимость выработки продукции на одного работника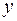 
(тыс. руб.) от ввода в действие новых основных фондов 
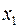(% от стоимости фондов на конец года) и от удельного веса рабочих высокой квалификации в общей численности рабочих 
(%).
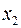Требуется:
1. Записать стандартизованное уравнение множественной регрессии. На основе стандартизованных коэффициентов регрессии и средних коэффициентов эластичности ранжировать факторы по степени их влияния на результат.
2. Рассчитать линейные коэффициенты частной корреляции и коэффициент множественной корреляции, сравнить их с линейными коэффициентами парной корреляции, пояснить различия между ними.
3. Составить уравнение линейной парной регрессии, оставив лишь один значащий фактор.
4. Построить линейную модель множественной регрессии. Найти коэффициенты парной, частной и множественной корреляции. Проанализировать их.
5. Найти скорректированный коэффициент множественной детерминации. Сравнить его с нескорректированным (общим) коэффициентом детерминации.
6. С помощью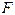 
-критерия Фишера оценить статистическую надежность уравнения регрессии и коэффициента детерминации 
.
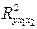7. С помощью частных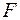 
-критериев Фишера оценить целесообразность включения в уравнение множественной регрессии фактора 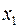после 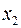и фактора 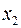после .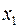
| Номер предприятия | 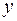| 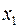| 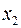| Номер предприятия | | | |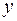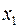
| 3,6 | 6,3 | ||||||
| 3,6 | 6,4 | ||||||
| 3,9 | |||||||
| 4,1 | 7,5 | ||||||
| 3,9 | 7,9 | ||||||
| 4,5 | 8,2 | ||||||
| 5,3 | |||||||
| 5,3 | 8,6 | ||||||
| 5,6 | 9,5 | ||||||
| 6,8 |
Типовой вариант индивидуальных заданий (ПК-9; ПК-10.)
1. По семи территориям Уральского региона за 2012 год известны значения двух признаков (табл.).
| Район | Расходы на покупку продовольственных товаров в общих расходах, %, y | Среднечасовая заработная плата одного работающего, руб., x |
| Удмуртская респ. | ||
| Свердловская обл. | ||
| Башкортостан | ||
| Челябинская обл. | ||
| Пермская обл. | ||
| Курганская обл. | ||
| Оренбургская обл. |
Дана модель парной (линейной) регрессии y=a+bx
Составить уравнение парной линейной регрессии
1) -8,22+0,7x;
2) 8,22-0,7x;
3) -0,7+8,22x.
2. Задача. По предприятиям региона изучается зависимость выработки продукции на одного работника 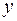(тыс. руб.) от ввода в действие новых основных фондов 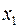(% от стоимости фондов на конец года) и от удельного веса рабочих высокой квалификации в общей численности рабочих (%).
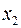Требуется:
построить модель с распределенным лагом, для l = 4, в предположении, что структура лага описывается полиномом второй степени. Определить стандартные ошибки коэффициентов модели. Проанализировать модель. Определить средний лаг и объяснить его экономический смысл.
| Номер предприятия | 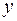| 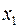| 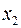| Номер предприятия | | | |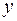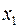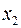
| 3,5 | 6,3 | ||||||
| 3,6 | 6,4 | ||||||
| 3,9 | |||||||
| 4,1 | 7,5 | ||||||
| 4,2 | 7,9 | ||||||
| 4,5 | 8,2 | ||||||
| 5,3 | 8,4 | ||||||
| 5,3 | 8,6 | ||||||
| 5,6 | 9,5 | ||||||
Тематика рефератов и творческих работ студентов:
1. Эконометрическое моделирование многоуровневых систем.
2. Эконометрическое моделирование региональной экономики.
3. Эконометрическое моделирование долгосрочного роста.
4. Интеграция эконометрических моделей и моделей общего равновесия/МОБа и программная реализация.
5. Дисперсионный анализ и его роль в исследовании взаимосвязей и взаимозависимостей социально-экономических явлений и процессов.
6. Роль и значение моделирования в экономическом анализе.
7. Эконометрические модели, их практическое применение.
8. Использование методов оценивания параметров моделей в эконометрическом анализе.
9. Оценка экономических структур. Практическое и экономическое обоснование критериев оценок.
10. Особенности моделирования производственных процессов и характеристика их оценок.
11. Изучение регрессионной связи показателей коммерческой деятельности.
12. Эконометрический регрессионный анализ макроэкономических моделей.
13. Однофакторный дисперсионный анализ деятельности фирмы.
14. Многофакторный дисперсионный анализ деятельности фирмы.
Перечень вопросов к зачету (с оценкой):
1. Эконометрическая модель. Исходные предпосылки эконометрического моделирования. Проблемы эконометрического моделирования.
2. Корреляционный анализ. Основные понятия. Корреляционная матрица. Мультиколлинеарность и способы ее устранения.
3. Исследование линейной зависимости У от единственной объясняющей переменной Х: парный линейный коэффициент корреляции. Поле корреляции.
4. Статистическое оценивание параметров. Статистические оценки и их основные свойства: состоятельность, несмещенность, эффективность.
5. Расчет и интерпретация коэффициента корреляции для парной линейной регрессии. Ко-эффициент детерминации и его характеристика.
6. Дисперсионный анализ: сущность и методика проведения. F- тест на значимость уравнения регрессии. Оценка точности уравнения регрессии.
7. Нелинейные регрессии и их характеристика. Регрессии нелинейные по переменным, но линейные по оцениваемым параметрам.
8. Линеаризация регрессий, нелинейных по оцениваемым параметрам. Критерии оценки.
9. Причины нелинеаризуемости моделей. Классификация оценки параметров нелинейных моделей. Критерии оценки.
10. Модели с лаговыми независимыми переменными. Основные подходы и процедуры оценки их параметров.
11. Модели с лаговыми зависимыми переменными. Проблемы оценки их параметров. Схема Койка.
12. Преобразование объясняющих переменных. Особенности определения ковариационной матрицы оценок коэффициентов.
13. Двухшаговый МНК и особенности его применения в моделях с лаговыми зависимыми переменными. Инструментальные переменные, их содержание и особенности формирования.
14. Экономический смысл главных компонент. Метод построения главных компонент.
15. Матрица главных компонент и ее связь с матрицей исходных факторов.
16. Моделирование временных рядов. Аддитивная и мультипликативная модель временного ряда.
17. Моделирование тенденции временного ряда. Основные типы трендов и их распознавание.
18. Выявление сезонной компоненты во временном ряду. Понятие автокорреляции и авторегрессии временного ряда. Виды автокорреляции.
Структурные и предопределенные переменные. Структурная и приведенная формы модели.
19. Общие понятия о системе одновременных уравнений (СОУ) и ее составляющие.
20. Формы представления системы одновременных уравнений.
21. Задача идентификации уравнений системы. Необходимое и достаточное условие иден-тифицируемости.
22. Оценки потерь в информации при использовании главных компонент. Применение метода главных компонент при построении моделей потребления продуктов питания.
23. Градиентные методы оценки параметров нелинейной модели и представления целевой функции. Построение оценки параметров градиентными методами.
24. Методы с производными и методы без производных. Построение процедур прямого поиска. Методы Гаусса и представление целевой функции.
25. Примеры моделей. Процедура оценки коэффициентов модели по методу Гаусса-Зайделя.
26. Оценка точности прогноза. Доверительный интервал прогноза. Интерпретация параметров модели.
27. Построение прогнозной процедуры и проблемы верификации прогноза.